При розробці ФДФ на пружно-демпферній підкладці основна увага приділяється деформаційним властивостям багато­шарової системи, а саме: особливостям перерозподілу деформацій між шарами ФДФ; відносній зміні розмірів друкуючого елемента; напруженням, що виникають у друкуючому елементі при його де­формації.

Для встановлення аналітичних залежностей розглянемо, насам­перед, деформаційний стан двошарової ФДФ на ділянках суцільних

Зображень (плашок).

Рис. 5.3. Схема двоша­рового зразка ФДФ

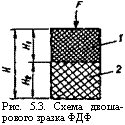На рис. 5.3 показано схему двошарового зразка ФДФ (ділянка плашки) заввишки Н з товщиною шарів Нх і Нт Матеріали шарів зраз­ка мають модулі еластичності Е1 і Ег На дру­куючий шар 1 з пружно-демпферною підклад­кою 2 діє сила Р з боку ЗМ.

При відносному стиску такого зразка на ДН шари деформуються на АНх і АН2, тобто

(5.22)

ДЯ = ДЯ, +АН2

У цьому разі у всіх перерізах зразка виникатимуть однакові за значенням напруження, тобто

Сгх= сг2 = а. (5.23)

Отже,

КАН. Е2АН2

А = - нГ = - нГ - (5-24)

Модуль еластичності полімерів залежить віц деформації стиску: ЕГДє,); £=/(є2). (5.25)

= е2_ нхан2 Е, Н2

Виходячи зі співвідношення (5.24), деформація одного з шарів

'кнГ' (5.26)

Замінивши ДЯ2 різницею (ДЯ — ДЯ,), рівняння (5.26) можна звести до такого вигляду:

Е2 НхАН-НхАНх

Ш'-і; н, ■ (5-я)

При цьому

(5.28)

£,Я2 +ВД

Розрахунок деформації шарів і напружень, що виникають у дво­шаровій ФДФ, за формулами (5.27) і (5.28) простий, але недосить точний при розрахунку деформованого стану друкуючих елементів, оскільки не враховується їхня конфігурація. Тому він може бути ви­користаний тільки для розрахунку форм-плашок.

Друкуючий елемент у двошаровій ФДФ має більше свободи в просторі для деформації, ніж її основа. При деформації друкуючого елемента в ньому виникають напруження, що залежать як від пруж­но-пластичних властивостей матеріалу, з якого він виготовлений, так і від його геометричних параметрів: ширини верхівки Ь, висоти Я,, кута нахилу бічних іраней а (рис. 5.4).

О

Для того щоб установити взаємозв’язок цих параметрів, уведемо величини, які характеризують напружено-дефор - мований стан (НДС) друкуючого елемента: Ь ширина контакту друкуючого елемента з ЗМ; а/<7= Г/(ЄІЬ)— відносне напруження, що вини­кає при деформації стиску по висоті друкуючо­го елемента завдовжки І, де — модуль зсуву.

При V = 0,5 модуль зсуву Рис. 5.4. Геометричні

Ці величини визначено для таких значень параметрів друкуючих елементів: Ь/Нх — від 0,2 до 5; а — від 60 до 90е; АНх / Нх — віц 0,03 до 0,3.

Аналіз результатів розрахунку показав, що друкуючі елементи з Ь /Нх < 0,4 віц стиску деформуються в різних напрямках друкуючої поверхні.

У подальшому, перетворивши здобуті залежності на зручну для оперування форму, були вибрані 50 найбільш характерних експери­ментальних точок всієї досліджуваної ділянки змінних а, Ь/Щ і АД/#і. Використовуючи ці дані, були побудовані такі регресивні моделі, що характеризують взаємозв’язок між всіма геометричними розмірами друкуючого елемента, його деформацією та напружен­нями:

=0,126- -0,0326—+0,00323а - -0,0024б( -]*; (5.30)

Я, в Я,<7 в Кв)

*=34,892-^+4,12^-0,382а^+32,329|^| ; (5 31)

В я, я, я, я, І я,) 'у--’1/

-^■100=6020,313^^-306,498-|-^^-62,416а^^ ; (5-32)

— 100 = 451,662—-18,005—— 11,007а—+1,89 іГ—1 £+0,07І8а2^. (5.33)

Ь С Я,<? в н,) в в

Аналіз реіресивних моделей показав, що деформація друкуючо­го елемента й напруження, які виникають у ньому, пов’язані між собою нелінійною залежністю.

При аналізі (5.32) та (5.33) було виявлено, що зміна ширини штриха деформованого друкуючого елемента пропорційна а/ <7 і

Другому степеню АНі ІН{. Після підстановки значення ДЬІЬ в (5.32) та (5.33) матимемо

Гі355-54—-33,021а+5,7~+(^2154а2)—=[-6020 -306,5—+62,416а1^2, (5.34) ^ я, я, ) в V я, )

Звідки

6020 — 306,5—+62,416а

___________ Я?_________

(5.35)

А=-

1355-54---- Зі021а+5,7—у+(^2154а2

Я, Я,

Де Е,=30.

252

Залежність (5.35) запишемо у вигляді

О=К'Еь$, (5.36)

Де К' — складна функція, аргументами якої є геометричні пара­метри Ь, Щ і а друкуючих елементів і яка визначається виразом

К'

1355 - 54-

Я,

-33,021а-5/7-^+0,215а2 Ні

6020 - 306,5—-62,416а _________________

(5.37)

Точність формули (5.36) нижча, ніж формули (5.31), здобутої внаслідок оперування з регресивними моделями (числова кореля­ція »0,75), але вона дає змогу якісно оцінити взаємозв’язок між деформацією друкуючого елемента та напруженнями, що виника­ють у ньому.

З (5.36) випливає, що деформація стиску друкуючого елемента по висоті й напруження, які виникають у ньому, пов’язані між собою геометричною прогресією.

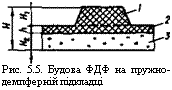
Поряд з вищевикладеним при розрахунку двошарової ФДФ слід мати на увазі, що її основа не є однорідною, а складається з пруж­но-демпферної підкладки З та прошарку 2, який з’єднує друкуючі елементи 1 і підкладку (рис. 5.5). Крім того, необхідно враховувати, що матеріал підкладки стискається.

Рис. 5.5. Будова ФДФ на пружно - демпферній підкладці

-і -2 З

______ і'-

«с:

Рис. 5.6. Схема ФДФ на пружно - демпферній підкладці у вигляді балки на пружній основі

Виходячи з цього, ФДФ на пружно-демпферній підкладці уяви­мо собі як балку на пружній основі (рис. 5.6). У цьому разі форму можна умовно розкласти на три основні складові частини: 1 — дру­куючий елемент завширшки Ь та заввишки Нї, який створює при деформації стиску навантаження на балку 2 заввишки А (роль ос­танньої у ФДФ на пружно-демпферній підкладці відіграє проша­рок, що з’єднує друкуючі елементи між собою та з підкладкою); З

— пружно-еластична основа заввишки Н2, що стискується, роль якої відіграє пружно-демпферна підкладка.

Відомо, що прогин балки на пружній основі визначається ви­разом
де знак «мінус» показує напрям прогину — донизу; Е — модуль Юнга балки; І — статичний момент інерції, а

W =e/b‘(cosyax + sinyax). (5.39)

Тут р — коефіцієнт, який залежить віц жорсткості балки та основи; х — відстань до точки прикладання сиди.

Якщо х = 0, то fix = 0 (W = і) і

У (5.40) К = Кх1, де / — ширина балки; Кх — коефіцієнт податли­вості основи, що дорівнює силі, яку треба прикласти до одиниці площі основи, щоб дати їй осідання на одиницю довжини, тобто

(5.41)

Якщо переріз балки вважати прямокутним, то

ІшЧ1 (5.42)

12

Тоді

Н1Н&- <5-43>

Із (5.24) та (5.41) маємо

Е-

(5-44)

Підставивши (5.44) у (5.43), дістанемо

Р е ь%нг' (5.45)

Після підстановки значень І та р у (5.38) за умови, що W = 1, знайдемо

Уш - l2F

[

Ч 3/4

Виходячи з того, що

У = 0(А> (5.47)

Де <т0 — напруження в основі друкуючого елемента (усереднена ве­личина), Ь0 — ширина його основи, причому

254

Ь=Ь+2Н№а, (5.48)

Вираз (5.46) запишемо у вигляді

У. ЕИгН2)

З іншого боку, якщо зробити припущення, що деформація стис­ку балки Дй = 0, матимемо

АЯ2 = АЯ-АЯ,=|>'|. (5.50)

Підставивши (5.48) у (5.49), дістанемо

ДЯ-ДЯ, =0)65О-0(Ь+2Я1с18а)|^- . (5.51)

Виходячи з того, що

СгЬ= о-Д, (5.52)

Знаходимо

(5.53)

У зв’язку з тим, що а визначається деформацією друкуючого елемента, перетворюючи (5.31) у зручний для подальшого викори­стання вигляд, маємо

<т=Гі 1,63+1,37—-0,І27а)^!-+І0>78^^.. /5 54)

V Я, ) Н Я, V • /

Після підстановки (5.54) у (5.53) остаточно знайдемо

АЯ = АЯ, +

+[(7^6+0,89Ь/Я, - 0,0826а)ДЯ, / Я, + 7,01ЛЯ,2 /Я,2] * ЕхЬ^$щ. (5.55)

Формула (5.55) встановлює взаємозв’язок між основними конст­руктивними розмірами ФДФ на пружно-демпферній підкладці, вла­стивостями матеріалів всіх її елементів і деформацією стиску ФДФ по висоті. Користуючись цією формулою, за допомогою ЕОМ мож­на визначити ДН, а підставивши це значення у (5.32), завчасно розрахувати збільшення ширини друкуючого елемента під час де­формації ФДФ на пружно-демпферній підкладці.

За допомогою наведених вище формул можна здійснювати вибір матеріалів для ФДФ на пружно-демпферній підкладці з урахуван­ням тиску на форму та деформації друкуючого елемента. Аналітич­на залежність (5.55) з досить високою для практичного використан­ня точністю описує НДС форми на пружно-демпферній підкладці завтовшки віц 0,2 до 1 мм. При збільшенні ширини друкуючого еле­мента відбувається більш складний розподіл деформацій і напру­жень в його основі, що призводить до зменшення точності розра­хунку. Ускладнювати ж формулу (5.55) для врахування спектра ширини штрихів друкуючих елементів (до Плашки) недоцільно, оскільки дрібні друкуючі елементи вигримують більш складні відносні деформації, ніж великі.

Якісний аналіз формули (5.55) показує, що значення АНи яке характеризує деформацію друкуючих елементів, тим менше, чим більше значення іншої складової цієї формули, що характеризує деформацію основи ФДФ на пружно-демпферній підкладці:

ДЯг = [(7,56+0,т/Н, -0,0826а)АЯ,/Я1 + 7,01АЯ,[1] /Я,2]хЦь |(5.56)

Як випливає з (5.56), основа ФДФ на пружно-демпферній підкладці деформується тим більше, чим більші розміри має друку­ючий елемент, чим більший модуль еластичності матеріалу, з якого він виготовлений, чим більша товщина підкладки і чим менші зна­чення кута нахилу бічних іраней друкуючого елемента, модуля ела­стичності матеріалу підкладки та жорсткості прошарку, що з’єднує друкуючі елементи з підкладкою.