РОЗРАХУНОК ОПТИМАЛЬНОГО ТИСКУ ДРУКУ
 21 сентября, 2013
21 сентября, 2013  admin
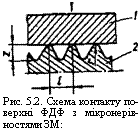
admin З літературних джерел відомо, що глибина вдавлювання еластоміра в нерівності твердого тіла описується рівнянням
Де V — коефіцієнт Пуассона; Р— нормальна сила, що діє на виступи нерівностей ЗМ; Ех — модуль еластичності полімеру; г
— радіус вершини виступу.
|
Рис. 5.2. Схема контакту поверхні ФДФ з мікронерів - ностями ЗМ: |
 Оскільки для полімерів, з яких виготовляють шар ФДФ, коефіцієнт Пуассона близький до 0,5, рівняння (5.1) набуває вигляду
Оскільки для полімерів, з яких виготовляють шар ФДФ, коефіцієнт Пуассона близький до 0,5, рівняння (5.1) набуває вигляду
5-м
2=0,683-
|
(5.2) |
![]() Щара - IV/! І-полімер; 2-ЗМ
Щара - IV/! І-полімер; 2-ЗМ
Кількість п виступів нерівностей ЗМ можна розрахувати за формулою (рис. 5.2)
А і2
Звідки
|
5 ’ Де р^ — загальна сила; І — відстань між виступами; 5і - яку діє загальна сила. Підставивши (5.4) в (5.2), дістанемо 2=0,683 (-1 /г- |
 (5.4) площа, на
(5.4) площа, на
Яр?**’ ^5'5^
Якщо середній тиск на друкуючий елемент з боку ЗМ виразити як
<г=^, (5.6)
|
Є = - |
![]() А відносну деформацію стиску матеріалу цього елемента — наближено як
А відносну деформацію стиску матеріалу цього елемента — наближено як
(5.7)
|
(5.8) |
![]()
|
Г=0,683 |
![]()
|
& |
![]()
|
Таким чином, глибина вдавлювання друкуючої поверхні без фарби в нерівності ЗМ пропорційна відносній деформації друкуючого елемента в степені 2/3. Ураховуючи те, що на друкуючому елементі міститься фарба, а під час здобуття відбитка має бути щільний контакт ФДФ з фарбою та ЗМ, в рівнянні (5.8) є виражатиме деформацію, що є наслідком відносного стиску ФДФ з фарбою. В цьому разі можна записати |
 То
То
Дя.+дя*
Є‘-Ц^-' (5-9)
Де Ни Нф— висота друкуючого елемента та товщина шару фарби на ньому; Кни АНф — абсолютні деформації стиску Ні і Нф.
Перетворивши вираз (5.9), дістанемо таку аналітичну залежність:
Є'н^іс/І'+*Н-)’ (5-10)
Де 3> £ф — відносні деформації стиску друкуючого елемента та фарби, що міститься на ньому.
Оскільки £ф можна виразити як рівняння пластичної деформації
*ф = 7г’ (5-11)
Де т — час дії навантаження, а 17 — коефіцієнт в’язкості фарби, вираз (5.9) матиме вигляд
Час дії навантаження
Т = В/У, (5.13)
Де В — ширина смужки контакту; V — лінійна швидкість друку.
З урахуванням (5.8) — (5.13) глибину вдавлювання друкуючої поверхні з фарбою у нерівності ЗМ можна записати так:
Із (5.14) випливає, що глибина вдавлювання, а значить і повнота контакту ФДФ з фарбою та ЗМ тим більші, чим менша динамічна в’язкість фарби і чим більша деформація друкуючого елемента. При сталому значені^ z збільшення в’язкості фарби потребує пропорційного збільшення модуля еластичності матеріалу друкуючого елемента.
Використовуючи (5.14) і вважаючи, що є= сг/ Еи можна розрахувати тиск, який необхідно прикласти до друкуючого елемента для забезпечення ефективної площі контакту ФДФ з фарбою та ЗМ:
К 1 чУ )
Де гри« — максимальна деформація вдавлювання або глибина мікро - нерівностей ЗМ.
Оскільки висота друкуючого елемента набагато разів більша від товщини шару фарби, можна вважати, що
(5.16)
Крім того, під дією тиску можуть частково вирівнюватися мікро - нерівності ЗМ, тому (5.15) матиме вигляд
|
|
Де 1/ — функція, якою враховують вирівнювання мікронерівностей ЗМ під тиском (при малих тисках XI4 0).
З (5.17) випливає, що при друкуванні на гладких матеріалах, коли / -> 0, тиск, необхідний для досягнення ефективної площі контакту між ФДФ і ЗМ, має бути близьким до нуля. При Нф-> 0, а також при ті -> 0 рівняння (5.17) набирає вигляду
|
|
(5.18)
Здобуті залежності стосуються ідеального друкарського контакту. Проте на практиці через використання малов’язких фарб і значні відхилення товщини ФДФ та друкарської пари тиск на ділянках дрібних штрихових зображень набагато перевищує потрібний, що призводить до появи графічних спотворень на відбитку внаслідок видавлювання фарби за краї друкуючих елементів.
Збільшення ширини друкуючого елемента на відбитку визначається виразом
|
|
Де / — коефіцієнт, який характеризує мікронерівності ЗМ; © — динамічний крайовий кут змочування ЗМ; Ь — ширина друкуючого елемента; В — ширина смужки контакту, що згідно з (4.19) визначається як
|
|
Де гф ц, гд ц — радіуси формного та друкарського циліндрів. 249
На підставі (5.19) можна визначити критичне значення тиску
А, при якому графічні спотворення друкуючих елементів (штрихів)
На відбитку не перевищуватимуть допустиме значення [ Ді7], тобто коли
Г
|
|
|
|
|
|
|
|
Таким чином, значення тиску має бути оптимальним з урахуванням конкретних умов друку. Недостатній тиск не дає змоги здобути повноцінний відбиток, а надмірний призводить до значних його графічних спотворень.

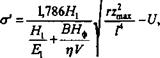
 Опубликовано в
Опубликовано в