Двумерные графические системы широко применяются при автома­тизации чертежных работ. Чертежи любой сложности строятся из базовых графических элементов: точек, прямых, окружностей и других кривых. Ка­ждый из этих элементов задается группой характерных точек, координаты которых могут определяться в абсолютной (мировой) системе координат или относительно предыдущей введенной точки (инкрементный ввод). При этом используют несколько способов задания точек:

• путем указания на экране с помощью мыши;

• путем введения чисел с клавиатуры;

• путем «привязки» к некоторому элементу чертежа, в окрестности которого располагается указатель.

Первый способ используют в основном для создания эскизов, а второй и третий — для построения точных изображений. Особенно удобным явля­ется третий способ, который позволяет «захватить» ближайший к курсору уже построенный элемент и ввести точные координаты конца или середины отрезка, центра окружности, точки пересечения прямых и т. д.

В средствах двумерной графики обычно имеется несколько способов построения одного и того же элемента. Например, отрезок можно построить по двум точкам либо по начальной точке, длине и углу наклона, а окруж­ность — по центру и радиусу, по трем точкам, по двум точкам и радиусу и т. д. Кроме того, в таких системах имеется ряд средств, автоматизирующих процесс черчения. Рассмотрим их подробнее.

Автоматическое построение скругления и фаски. Для получения скруглення или фаски необходимо указать мышью на стороны угла и ввести значение радиуса скругления или размер фаски. Отрезки на стыке угла и скругления (фаски) автоматически «срезаются» (рис. 1.2).

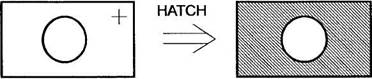
Автоматическая штриховка и закраска. Для получения штриховки надо ввести угол и шаг штриховки, а затем указать мышью на внутреннюю часть области, которую надо заштриховать. Аналогично выполняется и за­краска (рис. 1.3).

Автоматическая простановка размеров. Для простановки размера необходимо указать образмериваемые элементы и точку уровня размерной линии. После этого система автоматически вычислит числовое значение размера, выведет его на экране и нарисует выносные и размерные линии (рис. 1.4).

На любом этапе выполнения компьютерного чертежа можно удалить и модифицировать графические элементы изображения. Обычно двумерные САПР позволяют выполнять следующие операции редактирования.

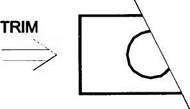
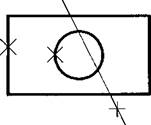
Отсечение. Эта процедура позволяет удалить лишние вспомогатель­ные линии на чертеже. Например, после указания мышью на секущую пря­мую и окружность из чертежа удаляется сегмент окружности. Такая же про­цедура может быть выполнена для любой комбинации графических элемен­тов (рис. 1.5).

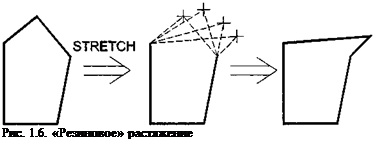
«Резиновое» растяжение. Процедура растяжения позволяет пользова­телю растягивать или сжимать изображенные на экране формы. Можно, в частности, с помощью мыши переместить любую из вершин ломаной. При этом в процессе редактирования перемещаемая вершина соединяется с сосед­ними при помощи пунктирных («резиновых») линий, а сразу же после отпус­кания кнопки мыши пунктирные линии заменяются сплошными (рис. 1.6).

Нанесение сетки. Для получения изображения с регулярной структу­рой удобно использовать сетку, которая позволяет указывать только на те точки экрана, в которых располагаются узлы. В таком режиме осуществля-

ется автоматический «захват» ближайшего узла и от конструктора не требу­ется очень точного указания точки. В результате можно легко ввести точки с заданным шагом. На твердую копию изображение сетки не выводится (рис. 1.7).

Построение сплайнов. В большинстве двумерных пакетов имеются средства для автоматической генерации гладких кривых (сплайнов), прохо­дящих через заданные точки. Такие процедуры очень удобны при создании нестандартных геометрических форм и позволяют дополнить автоматизиро­ванное черчение элементами автоматизированного проектирования (рис. 1.8).

Увеличение и панорамирование. Средства увеличения разрешают уве­личить или уменьшить любую область чертежа для более подробного про­смотра или редактирования. Чтобы проанализировать другие элементы чер­тежа, область просмотра может быть панорамирована (сдвинута) в любом направлении, что позволяет использовать один сборочный чертеж для изде­лий любого размера и сложности, отказавшись от множества небольших чертежей, как принято в традиционном черчении. При необходимости мож­но получить твердую копию любой области чертежа (рис. 1.9).

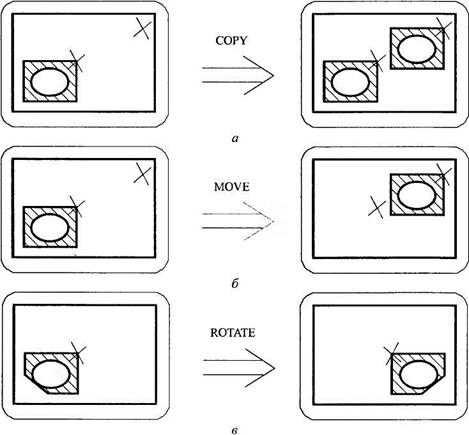
Копирование, поворот и перенос. Любой элемент изображения или группу элементов можно скопировать, переместить и/или повернуть. Для двумерного поворота достаточно задать положение центра вращения и угол поворота. При переносе обычно вводятся две точки, определяющие вектор смещения. Перенос и поворот, а также копирование широко применяются при вставке в чертеж стандартных элементов, вызываемых из стандартных библиотек (рис. 1.10).

Рис. 1.8. Построение сплайна

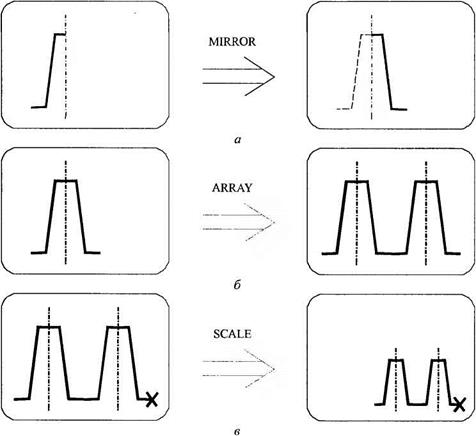
Преобразования. Кроме поворота и переноса многие графические па­кеты имеют и более сложные средства манипулирования изображением: зеркальное отражение и пошаговое размножение. Используя эти средства, очень удобно строить чертежи регулярных структур. Например, для созда­ния чертежа зубчатой рейки достаточно построить половину профиля одно­го из зубьев, далее применить операцию зеркального отражения, а затем размножить полученный образ. Можно также провести масштабирование изображения (рис. 1.11).

Выбор элементов и объединение их в группы. В большинстве графиче­ских пакетов операции редактирования могут выполняться как над отдель­ным элементом, так и над группой элементов. Например, для сдвига части чертежа нет необходимости перемещать все элементы по отдельности. Вме­сто этого достаточно «выбрать» их путем указания на каждый из элементов либо осуществить «окн про ванне» (выделение на чертеже прямоугольной области, все элементы которой выбираются автоматически). В дальнейшем операции редактирования производятся одновременно над всеми элемента­ми полученного набора. Можно, например, изменить цвет и тип линий всех элементов, произвести масштабирование и т. д.

Иногда удобнее объединить выбранные элементы в группы (блоки). В результате получается составной графический элемент, который при редак­тировании рассматривается как единое целое. В группы можно объединять и составные элементы, образуя многоуровневые иерархические структуры. При необходимости можно выполнить и обратную операцию — разделить составной элемент на отдельные составляющие.

Расслоение. Во многих двумерных САПР реализован принцип «рас­слоения», позволяющий разделить чертеж на несколько частей, наложенных друг на друга. С точки зрения традиционного черчения это эквивалентно созданию нескольких чертежей, каждый из которых выполнен на прозрач­ной пластине. Причем можно рассматривать каждую пластину по отдельно-

Рис. 1.10. Копирование (а), параллельный перенос (б) и поворот (в)

сти либо, складывая их, получать совместное изображение. При выполнении чертежей механических конструкций можно, например, разместить все гео­метрические элементы в одном слое, а все размеры и пояснительные надпи­си — в другом.

Двумерные системы позволяют построить упрощенные геометриче­ские модели реальных физических объектов, состоящие из трех независи­мых проекций (видов). При их использовании модель куба, например, зада­ется 12 двумерными точками с координатами XY. Поэтому при внесении изменений конструктор должен редактировать отдельно каждую из проекций.

В трехмерных системах используются точки с тремя координатами, что позволяет автоматически устанавливать проекционные связи. Так, в этом случае куб описывается восемью трехмерными точками XYZ, по кото-

Рис. 1.11. Зеркальное отражение (а), размножение (б) и масштабирование (в)

рым находятся проекции XY, YZ и XZ. При использовании таких систем обычно начинают с построения трехмерного изображения, а двумерные ви­ды формируются на последнем этапе, при выводе чертежей. А в некоторых случаях двумерные чертежи полностью заменяются трехмерной компью­терной моделью, по которой генерируются программы для станков с ЧПУ.

Системы трехмерного моделирования широко применяются в интег­рированных САПР/АСТПП. Они часто дополняются средствами автомати­ческого анализа физических характеристик (вычисление массы, центра масс, моментов и тензоров инерции и др.), а также модулями, обеспечивающими оценку прочности и технологичности. Использование трехмерных систем в настоящее время уже не сдерживается стоимостью программных средств и оборудования.

Пустые “Заполненные’

Элементы модели грани

а

б

в

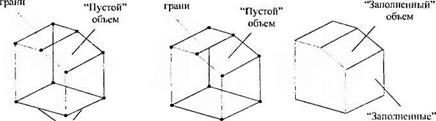
Рис. 1.12. Геометрические модели трехмерных объектов: а — каркасная (Wire-frame); б — поверхностная (Surface); в — твердотельная (Solid)

Методы трехмерного моделирования, используемые в САПР, делятся на три группы: каркасное, поверхностное и твердотельное (сплошное) моде­лирование (рис. 1.12).

Каркасное моделирование (рис. 1.12, а). Модель каркасного типа пол­ностью описывается в терминах точек и линий. Ее главным достоинством являются простота и невысокие требования к компьютерной памяти, а не­достатки связаны с отсутствием информации о гранях, заключенных между линиями, и с невозможностью различить внешнюю (незаполненную) и внутреннюю (заполненную) области. Наиболее широко каркасное модели­рование применяется при имитации несложного пространственного движе­ния инструмента (например, при фрезеровании по трем осям).

При использовании каркасных моделей в САПР необходимо учиты­вать следующие ограничения:

• неоднозначность — отсутствие возможности однозначно оценить ориентацию и видимость граней, что не позволяет различать виды сверху и снизу, а также автоматизировать удаление скрытых линий;

• приближенное представление криволинейных граней — невоз­можность точно описать криволинейные поверхности (цилиндры, конусы и др.), которые реально не имеют ребер; иногда для таких поверхностей вводят фиктивные ребра, располагаемые через регулярные интервалы (рис. 1.13);

• невозможность обнаружить столкновения — отсутствие информа­ции о поверхностях, ограничивающих форму, не позволяет обнаружить столкновения между объектами, что важно при моделировании роботов, проектировании планов размещения оборудования и т. д.;

• погрешности оценки физических характеристик — возможность некорректного вычисления массы, центра тяжести, момента инерции и

Рис. 1.13. Приближенное представление криволинейных поверхнос­тей в каркасных моделях (вводятся фиктивные ребра)

т. д., обусловленная недостатком информации об ограничивающих по­верхностях;

• отсутствие средств «затенения» поверхностей — у модели, со­стоящей только из ребер, невозможно произвести закраску поверхностей различными цветами.

Поверхностное моделирование (рис. 1.12, б). Модель поверхностного типа описывается в терминах точек, линий и поверхностей. В отличие от каркасной модели она обеспечивает:

• точное представление криволинейных граней;

• автоматическое распознавание граней и их закраску,

• автоматическое удаление невидимых линий (рис. 1.14);

• распознавание особых линий на гранях (отверстий и т. д.);

• обнаружение столкновений между объектами.

Метод поверхностного моделирования наиболее эффективен при про­ектировании и изготовлении сложных криволинейных поверхностей (кор­пусов автомобилей и др.). При этом можно использовать:

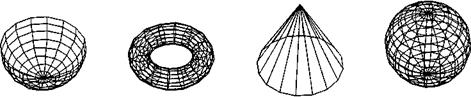
• базовые геометрические поверхности (плоскости, цилиндры, кубы, результат перемещения образующей кривой в заданном направлении и т. д., рис. 1.15, а);

• поверхности вращения (результат вращения линии вокруг оси, рис. 1.15, б);

• пересечения и сопряжения поверхностей',

• аналитические поверхности (задаются математическим уравнением);

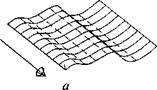
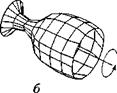
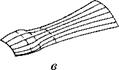
Рис. 1.15. Поверхностные модели, полученные путем перемещения кривой в заданном направлении (я), вращения кривой (б) и при по­мощи сплайн-интерполяции (в)

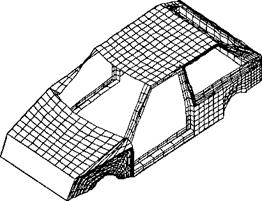
• скульптурные поверхности или поверхности «свободных форм», ко­торые не могут быть описаны одним математическим уравнением, а задают­ся при помощи методов сплайн-интерполяции образующих кривых (корпуса автомобилей, фюзеляжи самолетов, лопатки турбин, рис. 1.15, в; 1.16).

В современных трехмерных системах широко используются состав­ные поверхности, составленные из криволинейных четырехугольников, ог­раниченных гладкими кривыми. Внутренняя область каждого такого участ­ка определяется путем интерполяции. При изображении составных поверх­ностей на экране создается сетка, натянутая на многогранный каркас.

На базе методов поверхностного моделирования построен ряд мощных графических систем, широко применяемых в промышленности. Однако поверхностные модели имеют ряд недостатков, которые могут быть устранены только в рамках твердотельного моделирования. К ним относятся:

• неоднозначность при моделировании реальных твердых тел;

• сложность процедур удаления невидимых линий и отображения внутренних областей.

Твердотельное моделиро­вание (рис. 1.12, в). Модель твер­дотельного типа описывает трех­мерный объем, который занимает рассматриваемое физическое те­ло. В отличие от каркасных и по­верхностных моделей она обес­печивает:

• полное описание запол­ненного объема и возможность разграничения внешних и внут­ренних областей, на основе чего

„ , ,, „ автоматизируется процесс обна-

Рис. 1.16. Поверхностная модель кузова г „

автомобиля ружения столкновении;

• автоматизацию процесса удаления скрытых линий;

• автоматизацию процесса построения разрезов и сечений, что требу­ется при создании сборочных чертежей сложных изделий;

• применение современных методов анализа конструкций (точное вы­числение массогабаритных характеристик, расчет прочности и деформаций методом конечных элементов и т. д.).

• эффективное управление цветами и источником освещения, получе­ние тоновых изображений;

• более точное моделирование кинематики и динамики многозвенных механизмов (роботов, станков и т. д.).

Существует целый ряд способов построения твердотельных моделей. Однако в САПР наибольшее распространение получили два из них: метод конструктивного представления (C-Rep) и метод граничного представления (B-Rep). Рассмотрим их подробнее.

Метод конструктивного представления (C-Rep) основан на создании моделей из типовых твердотельных примитивов с заданными размерами, ориентацией и точкой привязки. При определении взаимоотношений между соседними примитивами используются булевы операции: «объединение», «разность» и «пересечение». Твердотельные примитивы могут выбираться из библиотеки или генерироваться путем движения произвольной поверхно­сти вдоль некоторой кривой. В результате происходит «захват» (sweeping) части трехмерного пространства, принадлежащей примитиву.

Метод граничного представления (B-Rep) также оперирует с примити­вами, связанными при помощи булевых операций. При этом модель описы­вается совокупностью ребер и граней, определяющих граничную поверхность твердого тела. Эти данные дополняются информацией о топологии примитива и особенностях его геометрии. Метод B-Rep более удобен при модификации примитивов, но требует большего объема компьютерной памяти.

Методы твердотельного моделирования, основанные на булевых опера­циях, особенно удобны при вычислении поверхностных и весовых характери­стик тел, расчете напряжений, имитации операций механической обработки. В последнем случае операции резания металла (точение, фрезерование, сверление и т. п.) могут быть легко описаны при помощи булевой разности. Естественным приложением булевой алгебры является также анализ столкновений (колли­зий), которые обнаруживаются при помощи операции пересечения.