Напряжение, подводимое к электродной проволоке и основному металлу при электрошлаковом процессе, создает в шлакооой в^нне электрическое поле, которое является источником тепловой энергии. Это поле можно представить с помощью числовых моделей его харак­теристик: распределения потенциала и объемной тепло­вой плотности. Количество теплоты, выделяемой в каж­дом элементарном объеме ванны в единицу времени, определяется дифференциальным уравнением Джоуля— Ленца:

Q = а£2,

где о — электрическая проводимость шлака; Е—вектор напряженности электрического ноля.

Таким образом, расчет объемной тепловой плот­ности сводится к налождению напряженности злекіри - ческого поля, которая в свою очередь определяется скоростью изменения скалярного потенциала поля:

Е = — grad ф.

Потенциал ф в каждой точке поля, не содержащего свободных зарядов, определяется уравнением Лапласа:

Д2ф — о.

В процессе наплавки проволочными электродами элек­трическое поле постоянно меняется из-за их неравно­мерного плавления и возникающей при этом темпера­турной неоднородности шлаковой ванны, которые зави­сят от материала и диаметра электродов, скорости их подачи и процесса каплеобразования.

Расчет реального поля такой ванны весьма сложен, поэтому электрическое поле электрошлаковой ванны рассчитывали в бесконечно малый промежуток времени,

когда его с небольшой поірешлостью можно принять стационарным. При этом сделали следующие допуще­ния: поверхность жидкого металла плоская, электро­проводимость шлака в любой точке ьанны постоянна, боковые стенки ванны неэлектропроводимы

Для условий наплавки эти допущения вполне пра­вомерны и мало искажают реальную картину: во-пер­вых, наплавка ведется гребенкой недалеко отстоящих друг от друга электродов, и ванна шлака прогревается достаточно равномерно; во-вторых, шлаковая ьанна при наплавке неглубокая (25—35 мм), с большой поверх­ностью контакта с жидким металлом, измеряемой сот­нями квадратных сантиметров, что способствует хоро­шему и равномерному прогреву; в-третьих, расстояние между осями отдельных электродов гребенки примерно иа порядок больше межэлектродного промежутка (расстояние от торца любого электрода до зеркал*, пенны жидкого металла); в-четвертых, в системе, как правило, активно плавится один, два электрода, под которыми возможно искривление поверхности жидкого металла, под остальными она плоская.

Распределение потенциала в таком поле подчи­няется двумерному уравнению Лапласа:

Д2ф = д2ц)/дх2 + (Ptyldy* = 0.

Рассчитываемую область поля разбивали на ячейки посредством квадратных сеток. Для каждой узловой точки потенциал определяли по расчетному уравнению в разностной форме для некоторой узловой точки 0:

фр + Фп + Фи + фс — 4фо = 0, (13)

где фр, фп, Фк, фг,— потенциалы б точках, сопряженных на сетке с точкой 0 (рис. 7).

Расчетное уравнение (13)—частный случай реше* ния уравнения Лапласа методом сеток. Полученное распределение потенциалов явилось основой для опре­деления напряженности в узловых точках по урав­нению

Е — — (т!(2а)) ((фр — фп) і + (фк — фс) /'),

где т — коэффициент напряженности, принятый для расчета потенциалов поля; а — сторона ячейки поля; і, / — единичные векторы.

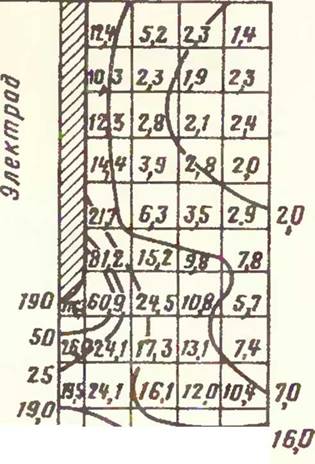
Рис. 7. Распределение потенциала и объемной тепловой плотности в электрошлаковой ванне с одним электродом

По величине напряженности поля в узловых точках сетки вычисляли объемную тепловую плотность, при этом напряжение, подаваемое на электрод, задавали в условных единицах, а произведение с{т/(2а))2 при­няли за единицу. Точки с одинаковыми значениями объемной тепловой плотности соединяли плавными линиями, общая картина которых изменялась при вве­дении постоянных коэффициентов. Это позволяет создать семейство числовых моделей для данной шла­ковой ванны при изменении в широких пределах зна­чения напряжения наплавки и проводимости шлакй и изучать тепловое поле шлаковой ванны в динамике. Кроме того, появляется возможность численно опреде­лить наиболее эффективные параметры процесса. При заданном напряжении наплавки V физическое распре­деление потенциала определяется умножением всех значений модели наї коэффициент т= | (УД/усл. од|- а распределение объемной тепловой плотности на ко­эффициент М = 0,06 а2[т2а.

Был проведен расчет числовых моделей шлаковой ванны глубиной 30 мм, диаметром 26 мм при исполь­зовании электрода диаметром 2 мм для напряжения.

равного трем условным единицам. На рис. 7, а дано распределение потенциала, в узловых точках сетки приведены его значения. На рис. 7,6 показано распре­деление объемной теплозой плотности, значения экви - тспловых линий вынесены за пределы сетки поля, мак­симальное значение объемной тепловой плотности на ходится на торце электрода.

В табл. 2 сведены - коэффициенты перевода условных единиц в физические для построения семейства число - пых моделей данной ванны. С увеличением напряже­ния наплавки и электрической проводимости шлака коэффициент М возрастает, а следовательно, увеличи - імется и объемная тепловая плотность. Визуальный Анализ модели (см. рис, 7,0) показывает, что эквитеп-

Габлица 2. Коэффициенты перевода условных единиц в физические для построения семейства числовых моделей электрошлаковой ванны с одним электродом Напряжение мплавкн, В Флюс Коэффициенты Марка Проводимость при 2000 сС. См/м Af-i 0і®. Дж/(с-м») m, В ФЦ-7 160 0.9 АН-348А 300 1.8 1А ОІІ АН-8М 350 2,1 IU АНФ-1 900 5.4 ФЦ 1 150 1.15 АН-348* 300 2,29 11 «Ї1 АН 8М 350 2,69 11 ,оо АНФ 1 900 6,93 У ФЦ-7 15С 1,44 QO АН-348А 300 2,9 to А7 иО АН-8М 350 3,37 іх,0/ АНФ-1 900 8,66 ФЦ-7 150 1.76 49 АН-348А 300 3,52 IА АН-8М 353 4,116 АНФ-1 900 10,58

Рис. 8. Зависимость в относи гел«ных переменных объемной тепло­вой плотности от глубины погружения электрода в шлаковую ванну:

I — расстояние между электродом и зеркалом жидкого металла ио оси ванны; 1Х —. расстояние рассматриваемой точки от зеркала жидкого метал­ла; Qmax — максимальное значение объемной тепловой плотности на торце электрода; Qx — объемная тепловая плотность ка расстоянии 1Х от зеркала жидкого металла

ловые линии у торца электрода представляют собой разрез замкнутых поверхностей, а тепловое поле на глубине ванны резко неоднородно. С увеличением глу­бины погружения электрода в шлак картина тепловою поля меняется.

На рис. 8 приведена зависимость, построенная в ко­ординатах: по оси ординат — отношение объемной теп­ловой плотности различных точек по оси ванны к ее максимальному значению (на торце электрода); по оси абсцисс — отношение расстояния рассматриваемой точ­ки от зеркала жидкого металла по оси электрода к рас­стоянию между электродом и зеркалом жидкого металла. Кривая А{ рассчитана для глубины погруже­ния электрода на 10 мм, кривая А2 — на 15 мм, кри вая Аз—на 20 мм. Относительное количество теплоты точек Аи А2у А3 равно 0,5. С увеличением глубины по­гружения электрода эта точка смещается к его торцу а следовательно, объемная тепловая плотность на торце электрода увеличивается. Известно [32], что при одном и том же напряжении электрошлакового процесса для увеличения глубины погружения электрода в шлак необходимо увеличить скорость его подачи. При этом скорость плавления электрода возрастает. Одной из причин этого является увеличение объемной тепловой плотности на его торце.

Чьслеььое решение задачи о протекании тока и

тепловыделении в шлаковой ванне с Омньм электродом

сводится к решению уравнения Лапласа для потен­циала на ванне Д£/=С с граничными условиями: U=Uo на электроде, <7=0 на поверхности металлической панны и dUfdz=0 на границе шлак—воздух. Решение уравнения Дф=0 для безразмерного потенциала

UJUo находилось как установившееся решение урав­нения

- 1 3 (г N і *ф

дг г дт дґ ) дгг *

которое аппроксимировалось по сетке уравнением

(фі./.Н*— Фі./.*)/т = (ф/.>—І. А + Ф^Ж. а)/^2 +

+ (11 — //(2r4)J фі-i./.fe—4<р{,/.*+ (1 4-1/(2rt)] i./.ft)//*,

а при г=0 — уравнением

(фо./.л+і — фс,/,*)/* = (4<pijrfe+i —4фС j9k+i)/P +

+ (Фм-і.*— 2фо,/.* + Ф0./+1.*)//2,

где т — шаг по времени; I — шаг по пространственным переменным.

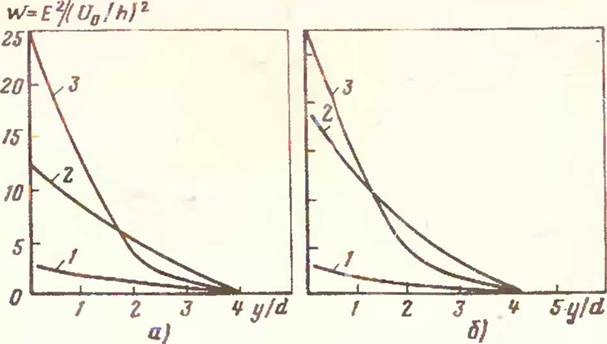
Оценивая спектральные радиусы соответствующих матриц, легко показать, что обе схемы устойчивы при т/Р<1/4. Вычисления проводили на ЭВМ при раз­личных погружениях электрода и диаметре d= *«0,1—0,5h (глубины ванны). На рис. 9 приведены зависимости плотности тепловыделения W=E2((Uolh)2 от расстояния до оси электрода (W — плотность тепло­выделения; Е — напряженность электрического поля в рассматриваемой точке; L/0 — напряжение на элек­троде; h — глубина шлаковой ванны). Полученная величина удобна тем, что описывает выделение теп­лоты во всех геометрически подобных шлаковых ваннах при сходстве формы плавящегося электрода.

Анализ результатов, полученных для различных глу­бин погружения, показывает, что наибольшую плот­ность тепловыделения имеет источник в области торца электрода. При этом размер области существенного тепловыделения равен примерно двум-трем диаметрам электрода.

Рис. 9. Плотность тепловыделения в шлаковой ванне с одним электродом в плоскостях, перпендикулярных его оси и располо­женных на два диаметра электрода выше (/), на два диаметра ниже (2); на уровне торца электрода (3): а — без шлакового гарнисажа на погруженном торце; 6 — со шлаковым гарнпсьжем. ГУБЯЩИЙСЯ торец электрода погружен на О. о глубины шла­ковой ванны

Увеличение глубины погружения ведет к росту ПЛОТ­НОСТИ тепловыделения под электродом, а темп роста выше вблизи дна ванны. Уменьшение диаметра элек­трода вызывает повышение плотности тепловыделения в области торца электрода. На основании опыта нами было учтено образование при большой подаче прово­локи в ванну изолирующей шлаковой прослойки на электроде вблизи верхней границы ванны. Задача была решена при измененном граничном условии. На рис. 9,6 приведена плотность тепловыделения для электрода, расположенного так же» как и в случае рис. 9, с, но подаваемого в ванну с большей скоростью и имеющем изолирующую шлаковую прослойку у верхней границы ванны. Анализ такого решения показывает, что плот­ность тепловыделения вблизи торца электрода воз­растает еще больше. Одновременно несколько увеличи­вается размер области существенного тепловыделения по оси электрода. Расчеты позволяют найти оптималь­ный межэлектродный промежуток, равный трем-четырем диаметрам электрода.

Указанная величина хорошо согласуется с опыт­ными данными, полученными при электрошлаковой на-

ІЛПііКе в нижнем положении (скорость подачи прово­куй 60 м/ч). При этом неравномерность проплавления наблюдается уже при межэлектродном промежутке, ранном шести-семи диаметрам электрода, и становится і* более значительной при дальнейшем увеличении лыо расстояния.

Анализ результатов счета для различных глубин «шгружения проволоки в шлаковую ванну показывает, ми - при увеличении «мокрого» вылета характер проте-* ft йшін тока и тепловыделение существенно не изме* Ntti >тся, однако значительно увеличивается плотность їчіловьіделения у дна ванны и на торце электрода. При межэлектродном промежутке, меньшем или рав­ном тром-четырем диаметрам электрода, плотность..ловыделения у дна шлаковой ванны уравнивается плотностью тепловыделения в области торца элек- г{*0ла. Это позволяет рекомендовать вести наплавку на t^wiix режимах, чтобы расстояние плавящегося торца МИКтрода до зеркала металлической ванны (дна шла - (мшпй ванны) было меньше четырех диаметров плавя - імоея электрода.

Описанные здесь расчеты проводились для электро­пил ковой сварки на постоянном токе. Б случае исполь - ♦ймния переменного юка плотность тепловыделения I нинне становится периодической функцией времени. Лыко показать, что средняя во времени плотность теп - імжиделения в такой ванне соответствует плотности п ювыделения в ванне при постоянном токе, одинакс - м*м напряжении на ваннах и cos <р= 1 для ванны пере - мишого тока. При cosq>^l плотность тепловыделения $ илнне переменного тока уменьшается пропорциональ - *■ • уменьшению COS ф.

Выполнено численное решение задачи о распределе­нии тока в ванне и особенностях тепловыделения в мно - электродной системе. При допущении постоянной Н|»жодимости шлака ток в ванне определяется реше­нном уравнения Лапласа для потенциала в ванне Миккиго металла Д£/=0 с граничными условиями ■ - Uq на плавящихся электродах, t/=0—на поверх­не л и металлической ванны и dUfdU на границе Идеик—воздух.

Уравнение Дф=0 для безразмерного потенциала *( (*♦ У* z)==U(x9 уу z)IUo решали на ЭВМ численным мигрированием по времени уравнения теплопровод-

W-E*/(Uc/h)

0

w-Ez/ayhiz

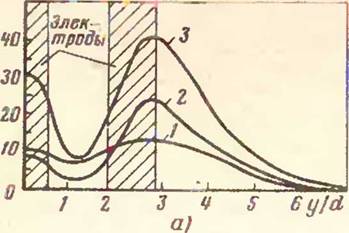
Рис. 10. Плотность тепловыделения в шлаковой ванне с т| электродами (1—3 см. на рис. 9) на расстоянии между осі электродов:

£► — 1,4 диаметра электрода; б — 3,5 диаметра электрода

ности <Зф/д/=Д<р до выхода решения на стационарна режим, когда <5ф/д*=0. При этом применяли схеГ «расщепления», сводящую решение ірехмерного ураї нения к решению последовательных одномерных за. Для прямоугольной ванны с тремя линейно расп< женными электродами вычисляли распределение тої число электродов в задаче увеличить трудно, так уже для уравнения с тремя электродами требует сетка с числом узлов ~ 15 ООО. ]

Зависимость плотности тепловыделения (£ — нап] женность электрического поля в точке) от расстоян] между осями электродов показана на рис. 10, а, б. Fj бина погружения электродов раьна 0,5 глубины шлаї вой ванны ft, диаметр электрода rf—0,1 Л и расстоян между осями плавящихся электродов 3,5d. Вычислен проводили также с другими глубинами погружения расстояниями между электродами. Анализ различж расположения электродов показал, что их взаимі влияние слабо зависит от глубины погружения в цш и сильно — от расстояния между их осями. В частносі при расстоянии, меньшем 2d, распределение тока зі чительно отличается от соответствующего распредеі ния на отдельном электроде. При расстоянии ме; осями плавящихся электродов Л/2 оно меняется сл; и совсем не меняется при расстоянии, большем П бины ванны. I

При сближении электродов плотность тепловьад^ ния вблизи торцов возрастает, а между электрода) выше торца уменьшается (рис. 10,а). Это приводі

if некоторому перемещению области существенного тмювыделения к поверхности металлической ванны. Меняется также характер тепловыделения у крайних іг»дтродов «гребенки». Плотность тепловыделения крайних электродов выше, чем у средних, а область •‘ущественного тепловыделения обладает большим Ьфактирным размером вследствие несимметричного

І

Шіфсния в область шлаковой ванны, свободной от іи ктродов. Это должно приводить к относительному перегреву шлака у крайних электродов системы и бо - лг« интенсивному плавлению их. Крайние электроды ріаливаются оплавленными всегда на большую высоту, средние.