Для полимерных материалов характерно не только вязкое, но и упругое поведе­ние (вязкоупругость). Например, этот тип поведения характерен для полимерного расплава на входе в каналы экструзионной головки при изменении поперечного сече­ния канала, в результате чего возникает перепад давления. Это происходит вслед­ствие деформирования расплава в переходах между участками с различными попе­речными сечениями канала. Часть полной деформации при этом составляют упругие деформации. На выходе из экструзионной головки упругие деформации проявляют­ся в виде изменения формы и размеров струи, называемое «разбуханием» экструда­та. Высвобождающаяся энергия упругих деформаций, образованная в результате работы перерабатывающего оборудования (например, экструдера), для системы те­ряется полностью.

Способность к обратимой деформации является следствием так называемой эн­тропийной упругости полимерных расплавов. Это означает, что макромолекулы, ко­торые изначально хаотично перепутаны (состояние максимального беспорядка — это состояние максимально возможной энтропии), могут в процессе деформирования
в значительной мере ориентироваться в направлении деформации. При этом полимер­ный расплав переходит в состояние, характеризующееся большей степенью упорядо­ченности и, следовательно, более низкой энтропией. Однако как только это происхо­дит, ориентированная сеть стремится вернуться обратно в состояние максимально возможного беспорядка (на основании второго закона термодинамики). Материал приспосабливается к возникшему деформированному состоянию, однако постепен­но происходит перегруппировка макромолекул (так называемая релаксация). По­скольку процесс снижения ориентированности макромолекул протекает медленно, он не завершается к моменту выхода материала из экструзионной головки. В резуль­тате процесс релаксации продолжается и после выхода материала из головки. Время, необходимое для завершения релаксации материала из ориентированного состоя­ния, сокращается с ростом температуры, поскольку в этом случае повышается под­вижность молекул и возрастает свободный объем.

Отмечено, что расплав «запоминает» деформированное состояние, которому он подвергался при прохождении через экструзионную головку. Это явление, называе­мое «эффектом памяти», характерно для вязкоупругих жидкостей.

Еще одной характерной чертой вязкоупругих жидкостей является наличие раз­ности нормальных напряжений при течении по криволинейным траекториям, а так­же сдвигом по фазе максимумов напряжений сдвига и скоростей сдвига при перио­дической деформации. Установлено, что эти максимумы не совпадают (например, [2-5,13,25]). Оба указанных явления используются при экспериментальном изуче­нии вязкоупругих жидкостей и определении характеристик полимеров.

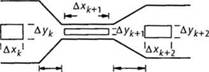
Когда полимерный расплав проходит через экструзионную головку, он подверга­ется деформациям двух типов (рис. 2.19 [30]):

Растяжение

Сжатие

SHAPE * MERGEFORMAT

Скорость продольной деформации = Сдвигающее действие

Рис. 2.19. Деформации растяжения

х

г. Д/' . Скорость сдвига е5 = — = у

и деформации сдвига, воз­никающие в результате разницы скоростей при продольном и сдвиговом течении [30]

• деформации вследствие растяжения или сжатия в сужающемся или расширя­ющемся участках канала соответственно; помимо этого, экструдат может под­вергаться свободному растяжению за пределами экструзионной головки;

• сдвиговой деформации вследствие развития профиля скоростей в канале.

В первом случае скорость продольной деформации определяется выражением

*-£. (2.36)

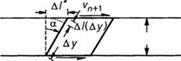
На рис. 2.19 показано, что единичный объем расплава за единицу времени скаши­вается на угол а вследствие разницы скоростей, существующей на его гранях. При непрерывном деформировании угол а стремится к 90 градусам, а смещение Д/+ в еди­ницу времени изменяется на А(Ду). Это означает, что сдвиговая деформация также может рассматриваться как способ ориентации макромолекулярных цепочек в на­правлении течения. Указанное явление описывается выражением

- t. (2.37)

Это предполагает возможность экспериментального измерения обратимой одно­осной деформации растяжения с помощью растягивающего реометра. При использо­вании такого прибора полимерная нить, например, растягивается при заданной тем­пературе и выдерживается в этом состоянии в течение нескольких периодов времени различной продолжительности. Затем полимерная пить оставляется в свободном со­стоянии и может свободно сжиматься [30, 31]. Обратимая деформация, возникаю­щая в результате свободной усадки и естественного увеличения диаметра нити, мо­жет быть определена с помощью меры Генки:

/(О

eR(t) = In - In XR(t), (2.38)

ос

где X — степень вытяжки; /(£) — длина образца после растяжения и выдержки в тече­ние времени t; 1Х — длина образца после полной усадки.

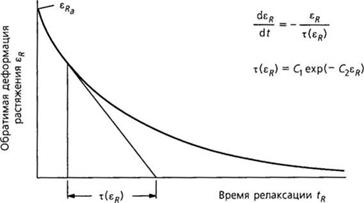
Этот принцип проиллюстрирован на рис. 2.20. Ослабление обратимой деформа­ции также определяется как релаксация. Предполагается, что общая деформация бу­дет полностью обратимой немедленно после ее приложения. При выдержке образца в деформированном состоянии начинает развиваться необратимая составляющая де­формации, величина которой представляет собой функцию времени. Доля необра­тимой деформации растет за счет снижения доли упругой деформации, иными сло­вами, за счет релаксации [30, 31]. Это уменьшение обратимой деформации во времени является функцией материала, температуры, а также начального уровня де­формации [30].

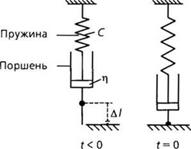
Проиллюстрировать изменение упругих и вязких свойств расплава удобно с по­мощью механической модели, состоящей из последовательно соединенных пружины и поршня (рис. 2.21). Нить полимерного расплава (аналогом которого является си-

Рис. 2.20. Изменение обратимой деформации растяжения во времени при постоянной температуре

стема «пружина-поршень») в момент времени t = 0 растягивается на длину Д/. Затем образец выдерживается в растянутом состоянии (положение системы «пру­жина-поршень» поддерживается постоянным). В течение этого времени в расплаве происходят релаксационные процессы (демпфер перемещается в продольном направ­лении). При длительном времени выдержки (Т -» оо) пружина вновь вернется в ис­ходное состояние. То есть энергия, затраченная в момент t = 0 для растяжения пружи­ны, изначально упругая, полностью преобразуется в энергию вязкого течения, что приводит к необратимой деформации поршня. Этому процессу соответствует кри­вая (рис. 2.20), обладающая характеристиками экспоненциальной функции, вид ко­торой может быть представлен уравнением [30,31 ]

deff ер

-т~ =----------- —---------------------------------------------------- . (2.39)

dt x(zr)

Рис. 2.21. Механическая модель «пружина-поршень», иллюстрирующая уменьшение упру­гих деформаций с течением времени

где т(ел) — время релаксации, являющееся функцией мгновенного значения дефор­мации cR.

Измерения показали, что это характерное время релаксации для различных тер­мопластов при различных температурах и различных значениях начальной деформа­ции хорошо аппроксимируется следующим выражением:

(2.40)

т(ел) = Сх ■ ехр(-С2 ■ er).

Здесь С, и С2 - характеристические константы материала [30,31].

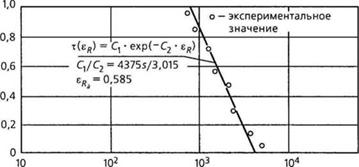
На рис. 2.22 показана нормализованная релаксационная кривая. Распределение характерного времени релаксации т(ел), полученное на основе этой кривой, показано на рис 2.23.

SHAPE * MERGEFORMAT

ш о X

о X

1,0

1 о о	I / 1 / 7-	тальное значение С,/С2 = 43755/	•; еЯа= 0,585 3,015
		о ° ч. ° о о

0,5

0

10

104

102 103 Время релаксации tR, с Рис. 2.22. Релаксация полистирола общего назначения (Г1С) при 130 °С

X к &

Характерное время релаксации т, с

Рис. 2.23. Характерное время релаксации как функция относительного упругого растяже­ния для ПС при 130 °С

<и I- s и о X »- О

Величина С, учитывает влияние температуры. Если ее значение известно для конкретной температуры, то его можно пересчитать для других температур расплава, используя простое уравнение температурного сдвига, подобное уравнению ВЛФ (по­скольку релаксация, как и течение, также основана на процессах межмолекулярного обмена [30]):

т(ед, Т) = С,(Г) ■ а^Т) • ехр(-С2 ■ ед), (2.41)

где ат - коэффициент сдвига для температурно-временной суперпозиции, который может быть вычислен с помощью одного из уравнений (2.19)—(2.22).

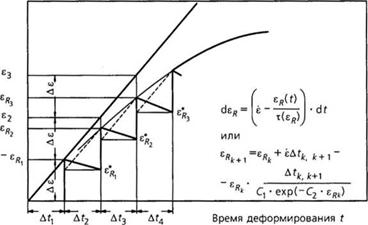
Одновременно с развитием обратимых деформаций (в результате сдвига или ра­стяжения) в полимерном материале развиваются релаксационные явления. Простое описание процесса развития обратимых деформаций дано в работах [30,31 ], где этот процесс интерпретируется как наложение уже существующих релаксирующих де­формаций на одновременно возникающие новые деформации (рис. 2.24). В течение интервала времени At{ внешнюю форму частицы расплава принимают неизменной, и начальная обратимая деформация за счет релаксации уменьшается со значения сш_{ до cRi_y По истечении интервала At{ скачкообразно добавляется дополнительная де­формация Ае, = е • tj+v являющаяся за счет этого полностью обратимой. Соотноше­ния, описывающие данную концепцию, приведены на рис. 2.24.

Q. С >

Рис. 2.24. Модель развития деформации при постоянной скорости деформации

5 X <и X сх ь го о. (X =т 05 Q. О •6- а> с[

Экспериментальные исследования с помощью растягивающего реометра показа­ли, что развитие обратимых деформаций хорошо аппроксимируется с помощью этой концепции, если шаг приращения времени Д£- достаточно мал. Этот подход может использоваться для моделирования не только деформаций при различных темпера­турах, но и для моделирования других типов деформаций. При этом для успешного моделирования необходимо соответствующим образом подбирать временной шагА£- и учитывать влияние температуры на релаксационное поведение с помощью коэффи­циента Cv

Эта модель, разработанная Вортбергом и Юн ком [30,31], была представлена здесь благодаря ее доходчивости и относительной простоты применения. Существует мно-

жество других моделей, также рассматривающих этот процесс. Некоторые из них описаны в работах, приведенных в списке литературы к главе [5,13,19,40,41][9].

Все модели имеют свои достоинства и недостатки, которые становятся особенно заметными при использовании в прикладных программах компьютерного модели­рования течения полимерных расплавов. В настоящее время еще не существует моделей, обеспечивающих удовлетворительную точность моделирования при описании поведе­ния расплавов различных полимеров, подверженных различным видам деформирова­ния (сдвигу, одно - или многоосному растяжению, а также различным комбинациям этих видов). Поэтому необходимо принимать во внимание все условия, с помощью которых разрабатывалась та или иная модель или определялись параметры конкретного материа­ла. Это позволит проводить анализ с учетом всех ограничений выбранного метода.