Вязкость и функции течения
 15 ноября, 2013
15 ноября, 2013  admin
admin При построении зависимости вязкости ц от скорости сдвига у на графике с логарифмическим масштабом по обеим осям получаем функциональную зависимость, справедливую для полимерных расплавов при постоянной температуре. График этой функции показан на рис. 2.1.
|
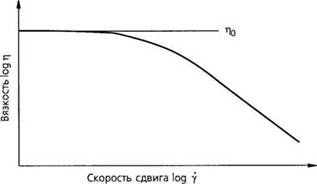
Рис. 2.1. Графическое представление зависимости вязкости от скорости сдвига (кривая вязкости) |
Как видно из графика, при низких скоростях сдвига вязкость остается постоянной или слабо уменьшается. Однако при достижении определенной точки вязкость начинает изменяться линейно в относительно широком диапазоне скоростей сдвига.
Это явление (то есть снижение вязкости с ростом скорости сдвига) называется псевдопластичностью. Постоянная вязкость, наблюдающаяся при низких скоростях сдвига, называется вязкостью при нулевом сдвиге (или наибольшей ньютоновской вязкостью) для данной температуры Г|0.
Графическое представление зависимости вязкости от скорости сдвига называется кривой вязкости. Используется также графическая зависимость напряжения сдвига от скорости сдвига в логарифмическом масштабе по обеим осям, которую называют кривой течения или реологической кривой (рис. 2.2). Для ньютоновской жидкости
|
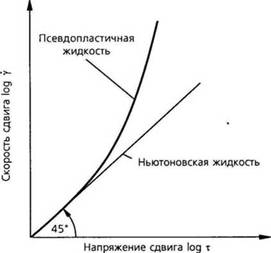
Рис. 2.2. Графическое представление скорости сдвига от напряжения сдвига (кривая течения) |
скорость сдвига прямо пропорциональна напряжению сдвига, т. с. график в двойных логарифмических координатах представляет собой прямую с коэффициентом наклона 1. Это означает, что угол наклона кривой течения к оси абсцисс составляет 45 град. Любое отклонение графика от этого значения указывает на неньютоновское поведение жидкости.
Для псевдопластической жидкости тангенс угла наклона больше единицы. Это значит, что скорость сдвига прогрессивно увеличивается с ростом напряжения сдвига. Соответственно, сдвиговое напряжение с изменением скорости сдвига возрастает медленнее, чем прямая пропорциональная зависимость (см. также главу 3.)

 Опубликовано в
Опубликовано в