УПРУГАЯ ПОДАТЛИВОСТЬ ПОЛЕЙ СОБСТВЕННЫХ НАПРЯЖЕНИЙ У КОНЦЕНТРАТОРОВ

7 сентября, 2014 Oleg Maloletnikov

На рис. 7.15 в качестве приме­ра показана растянутая в верти­кальном направлении пластина с почти круглым (t/p = 1,1) отвер­стием в середине поперечного се­чения, ширина которого 2B в 5 раз больше горизонтального размера отверстия 2t.

Формулы для вычисления на­пряжений у такого отверстия были приведены в разделе 3.1.3 под но­мером (3.20). Здесь нам нужна толь­ко формула для вычисления напря­жений аг:

Gx(y)= p ■ A ■ F(q>, x),

= 1,049;

где

1/2

Ф

A = -

= 214,881;

(ф-1)-(ф2 -1)

y1(y)== (у -1,1);

Му)+ф2]

х(у) =

V(y1(y))2 +ф2-[2-У1(у) + 1]

1

F(ф, X) = (Х(У))3 +Х(у)-(ф2 -ф-3) + ф +1.

Формулы (3.20) получены для отверстия в бесконечной пла­стине. Для пластины ограниченной ширины их нужно протари - ровать так, чтобы эпюра напряжений на рис. 7.15 уравновешивала

внешнюю нагрузку. Для этого вместо средних напряжений p нуж­но подставить Р0, при которых эпюра напряжений уравновешива­ет внешнюю нагрузку. Условие равновесия для половины нетто - сечения можно записать в виде

Р0 • (B -1) = (у) • dy,

5,5

откуда:

УПРУГАЯ ПОДАТЛИВОСТЬ ПОЛЕЙ СОБСТВЕННЫХ НАПРЯЖЕНИЙ У КОНЦЕНТРАТОРОВ

Р0 =

(5,5 -1,1)

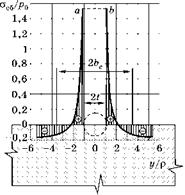
Рис. 7.16

Распределение собственных напряжений по краю полу­плоскости

(у) • dy = 1,224p.

1,1

Эпюра напряжений, изобра­женная на рис. 7.16, вычислена по формуле

°х (у)

Р0 1,224 • p,

где уx(y) вычислено по формуле

(3.20).

Чтобы получить из этой эпюры эпюру собственных напряжений, уравновешенную в пределах конст­рукции, нужно из нее вычесть p0. Это равносильно сдвигу начала ко­ординат рис. 7.15 вверх на единицу.

Эпюра собственных напряже­ний представлена на рис. 7.16. Для приближенного вычисления упру­гой податливости к краю полуплос­кости, изображенному на этом рисунке, нужно приложить нагруз­ку, равную собственным напряжениям: q(y) = стсб(у) = ах (у) - p0. Но как при этом смоделировать отверстие шириной 2t? Чтобы металл в районе отверстия не сопротивлялся прогибу кромки пластины, его нагрузили по пунктирной линии a-b (рис. 7.16) нагрузкой q(y), равной максимальным собственным напряжениям у отверстия. В итоге, нагрузка на кромку полуплоскости задана формулой

°x (|y|)

po

-1

po

q(y) = if f|y|< t, ^ -1,

po

Перемещение кромки пластины под этой нагрузкой вычисля­ли на основании формулы (7.18):

b

Ux (bc, у) ■ E po - Р

q(5)

po

2

Я

ln(y -$) - d$,

а упругую податливость в безразмерном виде по формуле

Ширина зоны разрушения be (ши-
рина упругопластической зоны) в этой
задаче определяется условием теку-
чести:

Gx (be ) —

Р0 Рo,

из которого можно (при заданном be)
вычислить уровень внешней нагруз-
ки Р0/^т.

График зависимости упругой по-
датливости поля собственных напря-
жений у круглого отверстия Al0 от
уровня внешней нагрузки Р0 в безраз-
мерном виде представлен на рис. 7.17.

Определим абсолютные величины
упругой податливости поля собствен-
ных напряжений у круглого люка диа-

метром 500 мм при напряжениях от полезной нагрузкиР0 = 0,75стт.

При Р0/стт = 0,75 из графика получаем:

Al0 E _ Alj 2,1 104

d/2 0,75-стт

3,2 • d/2 • 0,75-стт E

Alo(be) _ E Р Р0

- 0,686 мм.

_ 3,2,

Из графика рис. 7.17 видно, что с увеличением нагрузки упру­гая податливость Al0 все время возрастает. Поэтому, если внеш­няя нагрузка не фиксирована, как, например, при испытаниях образцов на разрушение, то верхней критической температуры для полей напряжений у концентраторов, показанной на рис. 7.10, не существует.

.

Опубликовано в ОСНОВЫ ТЕОРИИ ПРОЧНОСТИ СВАРНЫХ КОНСТРУКЦИЙ
«
»

Комментарии закрыты.