2.1. ЭЛЕМЕНТЫ ТЕОРИИ ТРАНСФОРМАТОРОВ

Трансформатор — это электрический аппарат, предназначенный для преобразования одного переменного напряжения в другое напря­жение той же частоты.

Трансформатор содержит две (или более) электрически не связан­ные между собой обмотки, размещенные на замкнутом стальном маг - нитопроводе. Для уменьшения потерь на вихревые токи магнитопроводы изготовляются из листовой электротехнической стали. В современных отечественных сварочных трансформаторах находит преимущественное применение холоднокатаная анизотропная рулонная сталь марок 3404, 3405 толщиной 0,35 мм и 3414 толщиной 0,35 и 0,5 мм с термостойким электроизоляционным покрытием, с содержанием кремния 2,8—3,8%, выпускающаяся по ГОСТ 21427.1—83.

По характеру устройства магнитной цепи различают трансформаторы броневого и стержневого типа, по характеру устройства обмоток — трансформаторы с цилиндрическими и дисковыми обмотками.

В источниках переменного сварочного тока преимущественное распространение получили трансформаторы со стержневыми магнито - проводами как с цилиндрическими, так и с дисковыми обмотками; трансформаторы работают с воздушным естественным или принуди­тельным охлаждением.

Трансформаторы с цилиндрическими обмотками (рис. 2.1,в), в которых первичные 1 и вторичные 2 обмотки наматываются кон­центрически одна поверх другой, относятся к группе трансформаторов с минимальным, или нормальным, электромагнитным рассеянием и яв­ляются полными аналогами силовых воздушных трансформаторов идентичной мощности.

Трансформаторы с дисковыми обмотками (рис. 2.1,6), в которых первичные 1 и вторичные 2 обмотки обычно разнесены относительно друг друга, относятся к группе специальных сварочных трансформа­торов с увеличенным, или развитым, электромагнитным рассеянием.

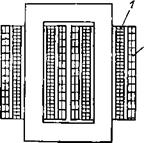
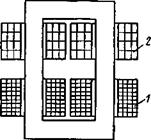
Рис. 2.1. Трансформаторы с цилиндрически ми (а) и дисковыми (б) обмотками

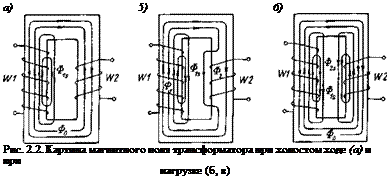
Анализ работы трансформатора со стальным магнитопроводом, имеющим переменную магнитную проницаемость, принято проводить на основе картины магнитного поля, схематически показанной для различных режимов работы на рис. 2.2.

Если при холостом ходе (вторичная обмотка разомкнута) к пер­вичной обмотке приложить переменное напряжение ы,, то она станет потреблять ток холостого хода іщ. Этот ток создаст переменный маг­нитный поток Фі.

Магнитный поток целесообразно разделить на две части (рис. 2.2, а): главный поток Фо и поток рассеяния Ф15. Главный поток замыкается по магнитопроводу и совпадает по фазе с реактивной составляющей тока холостого хода JIp, т. е. намагничивающим током. Связь между главным потоком и намагничивающим током определяется кривой намагничивания стального магнитопровода. Поток рассеяния Ф|, замы­кается по параллельному пути через воздух, прямо пропорционален первичному току и совпадает с ним по фазе.

Коэффициент пропорциональности между потокосцеплением и то­ком определяет индуктивность, и в данном случае индуктивность рассеяния первичной обмотки трансформатора Lls = w, Ф1Г//1.

В передаче мощности от первичной обмотки ко вторичной участвует только главный поток.

ЭДС самоиндукции в первичной обмотке можно также разложить на две составляющие: ЭДС, индуктируемую главным потоком, е х =

-~wi - г* и ЭДС, индуктируемую потоком рассеяния, є., - - L ~ .

at 14 14 at

Приложенное к обмотке напряжение и і уравновешивает падение напряжения на активном сопротивлении обмотки г і и наводимые в ней ЭДС.

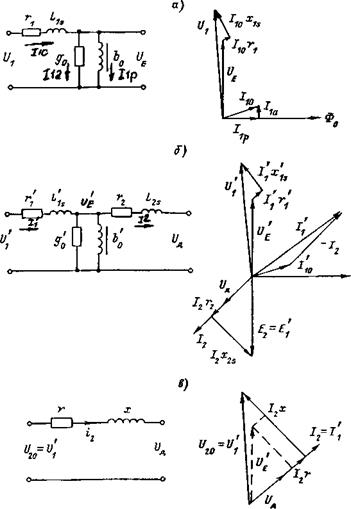
Заменив кривую тока /10 эквивалентной синусоидой, пользуясь символическим методом и обозначив через Щ составляющую напряже­ния, уравновешивающую ЭДС Ех, можно записать уравнение равновесия напряжений, построить схему замещения и векторную диаграмму транс­форматора при холостом ходе (рис. 2.3, а).

Уравнение равновесия напряжений

Ц = f їЛо 7 biLys I io + Uj?> (2-0

где UE = - k2.

Активная проводимость g0 (рис. 2.3,а), связанная с мощностью потерь в магнитопроводе Рс на гистерезис и вихревые токи, равна

So —IalUE =PC/UE.

Реактивная проводимость обмотки Ь0 для намагничивающего тока

&о =^ipWe ~ho/UE, так как обычно/1р іа.

Для удобства анализа работы трансформатора под нагрузкой при­нято приводить обмотки к одному числу витков. Операция приведения состоит в замене одной из обмоток эквивалентной обмоткой с числом витков, равным числу витков второй обмотки, причем такая замена не должна отразиться на режиме работы первой обмотки.

Из теории трансформаторов [23] известно, что при приведении вторичной обмотки к числу витков первичной обмотки параметры эквивалентной обмотки, обозначенные индексом ’’штрих”, связаны с параметрами основной обмотки следующими соотношениями:

е'г — пег i’i=hln r'2=r2n2-, L’2s=L2sn2,

где п = wltw2 — коэффициент трансформации.

При приведении первичной обмотки ко вторичной

е — е!п /'1=/'іл; г[=г2/п2 Ls=Llsjn2.

После приведения можно производить непосредственное сравнение ЭДС и токов в разных обмотках.

Заменим дуговое напряжение эквивалентной синусоидой и, учи­тывая, что оно совпадает по фазе со сварочным током, примем нагрузку сварочного трансформатора чисто активной. Прн нагрузке с ростом

Рис. 2.3. Схемы замещения и векторные диаграммы трансформатора при холостом ходе (а) и при нагрузке (б, в)

тока і2 должен увеличиваться и ток ilt при этом согласно выражению (2.1) должно снижаться напряжение Щ.

В трансформаторах с нормальным рассеянием, где падения напря­жения на активном г і и индуктивном xls = uLls сопротивлениях малы по сравнению с Щ, можно считать, что главный поток трансформа­тора при его нагрузке от холостого хода (/2 = 0) до номинального режима (/гном) практически не меняется. Следовательно, для возбужде­ния основного потока при нагрузке необходим практически тот же намагничивающий ток, что н при холостом ходе. Разница между первич­ным и вторичным токами всегда должна быть такой, чтобы обеспечить намагничивающий ток, необходимый для возбуждения основного пото­ка, что предопределяет автоматическое увеличение с ростом /2 ■

В трансформаторах с развитым электромагнитным рассеянием, где падение напряжения на сопротивлении xlf соизмеримо с величиной Щ = - Ei, рост тока нагрузки приводит к определенному снижению основного потока и намагничивающего тока.

Реальная картина электромагнитного поля трансформатора с раз­витым рассеянием (с разнесенными обмотками) схематически показана на рис. 2.2, б. При появлении тока i2 начинает сказываться его размагни­чивающее действие, которое заключается в том, что часть силовых линий потока, выходящего из зоны магнитопровода, связанной с пер­вичной обмоткой (Фі - Ф2), вытесняется из зоны магнитопровода, связанной со вторичной обмоткой. В результате при росте токов /2 и і і, помимо некоторого снижения ЭДС Еу, обусловленного рассеянием первичной обмотки, вследствие снижения потока Ф2 существенно умень­шаются ЭДС, наводимая во вторичной обмотке, и, следовательно, напря­жение на нагрузке (сварочной дуге).

Однако анализ работы и расчет трансформатора упрощаются, если реальную картину поля заменить эквивалентной (см. рис. 2.2, в), кото­рая строится в предположении, что главный поток, замыкаясь только по магнитопроводу, сцепляется со всеми витками первичной и вто­ричной обмоток. При этом имеют место два самостоятельных потока рассеяния Ф15 и Ф2s, причем поток Ф 2) в магнитопроводе условно направлен навстречу основному потоку. Тогда с учетом приведения ко вторичной цепи уравнения равновесия напряжений в трансформаторе запишутся в следующем виде:

U[ = r'li, i+iuL[,i[ + U^,

Ej = г2І2 +jbiL2sI 2 + Ua,

причем Ug = - Е = - Ei; І[о = 1[ -12.

Этим уравнениям соответствуют схема замещения и векторная диаграмма, приведенные на рис. 2.3, б.

Если пренебречь током холостого хода, который составляет 5-7% от номинального первичного тока, можно составить упрощенные схему замещения и векторную диаграмму трансформатора (рис. 2.3, в). На схеме и диаграмме г = r + r2; х = хs + x2s h = I[; U20 = U. Штри­ховой линией на диаграмме показан вектор Ug. Основания перпенди­куляров, опущенных из конца этого вектора на векторы 12х и 12г, показывают, как распределены активные и индуктивные падения на­пряжений между первичной и вторичной обмотками.

Векторные диаграммы (рис. 2.3, б, в) характеризуют работу транс­форматора в одном определенном режиме нагрузки (t/д, /2).

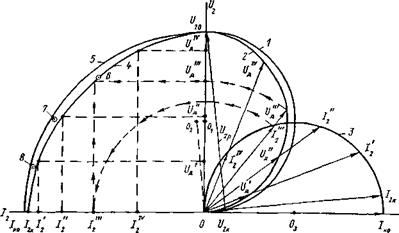
О том, как меняются соотношения величин в трансформаторе при изменении нагрузки (1/д) от холостого хода до короткого замыкания, можно судить по круговой диаграмме, которая для упрощенной схемы замещения представлена на рис. 2.4.

При коротком замыкании (С/д = 0; /2 = /2к) активные падения напряжения в трансформаторе определяются вектором t/2a = С/2к = = /2кг, а реактивные — вектором U2p = 12кх. Эти векторы взаимно перпендикулярны и являются катетами прямоугольного треугольника С гипотенузой U20.

При различных режимах нагрузки... ,uj^) вершина тре­

угольника перемещается по окружности 1, которая является геометри­ческим местом КОНЦОВ векторов U2а = t/д + 12г.

Геометрическим местом КОНЦОВ векторов t/д является окруж­ность 2, эксцентрическая относительно окружности 1. При построении окружности 2 следует учитывать, что при холостом ходе С/д = t/jo й, сле­довательно, окружность должна проходить через конец вектора С/20, а при коротком замыкании С/д = 0 и С/2а = С/2к и, следовательно, окруж­ность должна проходить через начало вектора С/2к и быть к нему каса­тельной. Для соблюдения этих условий необходимо, чтобы ее центр Ог лежал на пересечении двух перпендикуляров: перпендикуляра к вектору С/20, проходящего через его середину, и перпендикуляра к вектору С/2к, восстановленного из его начала.

От окружности напряжений, построенной на векторе С/20 как на диаметре, можно перейти к окружности токов 3. Диаметр этой окруж­ности будет представлять собой вектор идеального тока короткого замыкания трансформатора /к0 = С/20/х. По фазе векторы токов совпа­дают с векторами напряжений дуги, а по значению могут быть найдены из соотношения /2 = (/2р/х; геометрическим местом концов векторов /2, так же как и С/2р, является окружность.

Рис. 2.4. Круговые диаграммы напряжений и токов и внешняя характеристика трансфо рматора

Каждому значению вектора тока 72,... ,7^ соответствует опреде­ленное значение вектора напряжения дуги 1/'я Взяв численные

значения этих векторов и перенеся их в координатную систему, по оси ординат которой отложены напряжения С/2, а по оси абсцисс — токи 72, получим внешнюю характеристику трансформатора 4, соответствующую его некоторому индуктивному сопротивлению х. Для наглядности внешняя характеристика построена в свободном втором квадранте системы координат. Техника построения внешней характеристики видна из рис. 2.4 (см. точку!/"',/2").

Кривая 5 является внешней характеристикой идеального транс­форматора, у которого г = 0. Очевидно, что внешней характеристике такого трансформатора соответствует уравнение эллипса с полуосями U20, 7к0, и зависимость тока /2 от напряжения дуги С/д выражается соотношением

h =/ко^1- (ия/и20)

На рис. 2.4 показаны точки 6-8, полученные по уравнению h =4оЛ - U7(С/дIU20y.

Поправочный коэффициент 1,17 [20] учитывает, что при построении векторных и круговых диаграмм фактическое напряжение на дуге было заменено эквивалентной синусоидой.

Отметим, что внешняя характеристика, построенная на рис. 2.4, по форме идентична для любых конструкций трансформатора. При этом у трансформаторов с нормальным рассеянием, где номинальный ток 72ном составляет 7—12% от тока 72к, внешняя характеристика в зоне рабочих токов является жесткой. У трансформаторов с увеличенным рассеянием, где номинальный ток может составлять до 80% от 72к, внешняя характеристика является падающей.

Регулирование тока в трансформаторах с механическим регулиро­ванием связано с изменением значения индуктивного сопротивления. Каждому значению х соответствует своя внешняя характеристика. В трансформаторах с электрическим регулированием внешняя харак­теристика является предельной естественной внешней характеристикой. Внутри зоны, ограниченной этой характеристикой, регулирование тока и формирование требуемых автоматических внешних характеристик источника производятся при помощи тиристорного или подмагничи - ваемого регулятора.