Все поверхностные и граничные явления, происходящие при неустановившихся состояниях на контактирующих поверхностях, имеют прямое отношение к свариваемым контактам. С этой точки зрения любой способ сварки давлением может быть назван кон­тактной сваркой, но собственно электрическая контактная сварка отличается тем, что через свариваемый контакт специально про­пускается электрический ток. Этот факт усложняет все поверх­ностные и граничные процессы в контакте, превращая их из фи­зико-химических в сложнейшие электрофизические и, наконец, в металлоструктурные.

Электрический свариваемый контакт или полностью определяет энергетику сваривания, или обеспечивает значительное влияние на тепловой процесс при сварке.

Для того чтобы правильно управлять технологией сварки, технолог-сварщик должен отчетливо представлять сущность элек - тротепловых процессов в контакте и правильно оценивать роль контактных сопротивлений.

К сожалению, до настоящего времени в сварочной литературе часто встречаются такие формулы для определения электрических сопротивлений контактов, которые следует считать неприемлемыми, так как они не отражают физических процессов, происходящих в контакте. Одной из таких следует считать формулу

Ru = г1к/Ра, (1.60)

где Як — электрическое сопротивление контакта. Ом; г, к — сопротивление контакта при единичной силе сжатия; Р — единич­ная сила сжатия; а — показатель степени, скрывающий влияние всех переменных — геометрических, поверхностных и любых других физических.

Формула (1.60) создана Хольмом — Чельчлином 60 лет назад и не для свариваемых, а для шинных контактов с болтовым креплением. Только для такого рода электротехнических контак­тов она и пригодна.

К сожалению, в современную сварочную литературу некоторые авторы настойчиво внедряют формулы, еще более лишенные всякого физического смысла:

Яд = ^24 + 60'5Мэ ' е-°'00014Р КГ6, (1.61)

где Яд — эквивалентная геометрическая составляющая полного сопротивления контакта листов при точечной сварке; и 6 — диаметр электрода и толщина листа.

Опасность и вредность формул типа (1.60) и (1.61) в том, что они внушают неискушенному технологу примитивные представ­ления о свариваемом контакте как о некоем стационарном соеди­нении. Эти формулы закрывают перед технологом все действитель­ные сложные взаимозависимости, благодаря которым величины электрического сопротивления контакта при одних и тех же силах сжатия могут отличаться на несколько порядков.

К настоящему времени достоверная теория электрических со­противлений свариваемых контактов разработана пока далеко не полно, и те теоретические материалы, которые излагаются ниже, могут считаться достаточными только для сегодняшней технологии.

Определим, что такое электрическое сопротивление металли­ческого контакта. Как видно, эта характеристика представляет собой частное от деления приложенного к контакту электрического потенциала UK на мгновенное значение силы тока через контакт / (Л те

Я„ = ujl (t). (1.62)

Ток через контакт может быть переменным, униполярным или постоянным.

Самое существенное заключается в том, что амплитудное зна­чение электрического потенциала прикладывается мгновенно, а сила тока, независимо от формы его кривой, нарастает во вре­мени при включении от нуля до его амплитудного значения. Время

установления силы тока — это сотые и тысячные доли секунды. И все же в момент t = 0, т. е. в момент включения UK, сила тока / = 0 и, соответственно, мгновенное значение контактного сопро­тивления должны получаться бесконечно большими, как это фор­мально следует из определения (1.62). В действительности это не так. Выше уже было показано, что задолго до момента включения тока механическая деформация в плоскости контакта вызывает целый ряд чисто электрических явлений. Электрический заряд экзоэлектронного облака, круговые микротоки различно дефор - I мированных микроконтактов, плазменные потоки от разрывов электрической связи оксидных пленок с металлом — все эти эф­фекты создают такую суммарную протийоэлектродвижущую силу, которая даже в момент включения, т. е. при t = 0, в значительной степени уравновешивает потенциал UK. Точные измерения, выпол­ненные в Институте электросварки С. Н. Мещеряком и И. В. Пен - теговым, показали, что контактное сопротивление, действительное в момент і = 0, оказывается значительно больше установившегося значения, но не бесконечно большим.

Следует подчеркнуть, что все физические микроявления в пло­скости контакта практически не управляются и не регулируются посредством макроскопических средств. Поэтому в технологиче­ской практике придают большое значение стабилизации состояния металлических поверхностей контактируемых деталей. Однако ни механические, ни химические способы зачистки металла не спо­собны устранить значительную геометрическую и физическую неопределенности поверхностей в зоне контактирования. Так, табл. 5 приложения, показывающая параметры шероховатостей, содержит элементы заметной неопределенности: достаточно по­смотреть на возможные размеры высоты и основания пирамид. Мало того, пирамидальное моделирование — это весьма идеали­зированное моделирование действительности. Механические свой­ства металла микропирамид тоже весьма неопределенны, так как зависят не только от степени искаженности и дефектности кристал­лических организаций, но и от степени насыщенности пирамид оксидными включениями.

Структурная нестабильность металлических поверхностей обус­ловливает и еще одну неопределенность — разброс значений удель­ного сопротивления пирамид. Так можно ли и нужно ли ставить задачу создания для технологов расчетных систем по определению электрических сопротивлений свариваемых контактов? Безусловно нужно, но не для расчетов. Это необходимо для того, чтобы расчет­ные формулы возможно более наглядно показывали взаимосвязь Друг с другом большого числа переменных, определяющих контак­тирование. Теоретические формулы должны показывать и все вероятностные неопределенности, которые могут помешать уста­новить действительные искомые характеристики. За многие десятки лет технологической деятельности автор не знает случаев, когда цеховой или лабораторный технолог производил бы расчеты

электрических сопротивле­ний холодных контактов и когда бы ему необходимы были эти расчеты.

Правильное же понима­ние физической сущности электротепловых процессов немыслимо без тех теоретиче­ских расчетных формул, ко­торые на сегодня могут счи­таться достоверными. При этом неоднократно приходит­ся прибегать к использова­нию понятий подобия и к некоторым аналогиям. Впол­не, например, допустимо про­вести аналогию между тече­нием по трубе вязкой жидкос­ти и течением электрического тока по проводу. Эту анало­гию рассмотрим с помощью трубной модели. Силовые ли­нии электрического тока можно уподобить струям ла­минарного потока вязкой жидкости (рис. 1.19, а). Эти струи встречают концентрированное со­противление своему движению относительно диафрагмы 1, встав­ленной в трубу (рис. 1.19, б), что приводит к искривлению струй. Если посередине диафрагмы вставлена решетка 2 (рис. 1.19, в), то происходит добавочное, уже микроскопическое искривление струй, и тем самым вводится дополнительное сопротивление дви­жению жидкости. Сопротивления диафрагмы и решетки сумми­руются. Удалить решетку — значит снять микрогеометрическое искривление и уменьшить общее сопротивление. Ликвидировать диафрагму — устранить вообще всякое местное концентрирован­ное сопротивление. Остается постоянно действующее, равномерно по длине трубы распределенное сопротивление трения жидкости о стенки трубы.

Обратимся к модели стыкового контакта, показанного на рис. 1.8. Относительно контурной площади контакта линии элект­рического тока искривляются так же, как струи жидкости, проте­кающей сквозь диафрагму. Что же касается группы элементарных площадок контакта А/4Г, то они обеспечивают такого же рода микроискривления линий тока, какие создает внутридиафрагмен - ная решетка в трубе для струй жидкости. Теперь видно, что общее, или полное электрическое сопротивление контакта можно предста­влять как сумму
где ггс — геометрическая составляющая полного сопротивления стыкового контакта RKC (эта составляющая определяется искрив­лением линий электрического тока, определяемым контурной пло­щадью контакта); гмг — внутреннее сопротивление контакта, ко­торое создается искривлением линий электрического тока при протекании через микроконтакты шероховатости. Равенство (1.63) соответствует случаю контактирования идеально чистых метал-, лических поверхностей.

Если же шероховатая поверхность к тому же покрыта физиче­ски ощутимым слоем оксида, то сумма (1.63) усложняется еще двумя слагаемыми: сопротивлением материала самой оксидной пленки гпл и полярным сопротивлением границы оксид — металл ггрт. Эта последняя составляющая полярна по той причине, что каждый оксид — это полупроводник, и на границе его с чистым металлом создается электронно-дырочный переход. Мало того, если где-то в плоскости контакта возник островок расплавленного металла, то и граница жидкого металла с твердым тоже представ­ляет собой полярное электрическое сопротивление. Всякая гра­ница структурно различных объемов в металле, а также граница химически различных веществ является физическим контактом. Само собой разумеется, что количественный учет сопротивлений гпл, гГрт и Других граничных сопротивлений очень сложен и тео­ретическим расчетам вообще не поддается. К счастью, расчеты этих сопротивлений практически не нужны. Однако помнить о су­ществовании этих сопротивлений необходимо, поскольку значи­тельный элемент нестабильности электрических, сопротивлений холодных контактов обусловливается именно оксидными и адсорб­ционными наслоениями на контактирующих поверхностях.

Если определить сумму тех главных и основных составляющих полного сопротивления контакта, о которых технолог должен пом­нить постоянно, то для стыкового контакта

Rkc ~ ггс Гмг - j - гпл. (1.64)

Расчет первой составляющей, как будет показано ниже, обес­печивается с достаточной инженерной точностью. Расчет второй составляющей, как уже отмечалось, содержит ощутимую неопре­деленность. Третья составляющая вообще, пока уверенному рас­чету не поддается.

Для отчетливого представления об электрических сопротивле­ниях контактов или целых фигур сложной формы, которые при­ходится подвергать нагреву, необходимо установить: что же такое есть «искривление линий электрического тока» и почему это опре­деляет местную концентрацию электрического сопротивления.

Если границы А и В (рис. 1.20) связаны силовыми линиями электрического поля, то сопротивление единичной трубки тока

В этой записи удельное сопротивление может быть переменным по длине трубки, Т. е. р = /j (х), а сечение трубки тоже пе­ременным в пространстве от А до В:

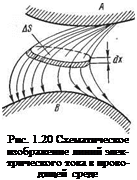&S = f2 (х),

тогда (1.65) перепишется так: в

_ Г, р (x)dx,,

ГеД_ J AS (ж) ' (1-66)

А

Отсюда видно, что большая кривизна трубки удлиняет путь тока от одной гра­ницы к другой, а этот факт и создает эффект возрастания электрического сопро­тивления.

Если р постоянно по всей длине и сечение трубки также по­стоянно, то

гед = рх/Д5, (1-67)

но это только при условии абсолютно равномерного распределе­ния тока по сечению трубки, что имеет место только для проволок или стержней, когда по ним протекает постоянный ток. Если же имеем, дело с более сложными геометрическими фигурами, то и при постоянном токе электрическое сопротивление вычислить пра­вильно по формуле (1.67) нельзя. К сожалению, этот принцип почти все технологи совершенно упускают из виду. 'Для того чтобы внести полную ясность в понятия электрических сопротивлений конкретных контактов и деталей, необходим подробный анализ распределения электрического тока в металле.

Рассмотрим несколько типовых токоведущих деталей.

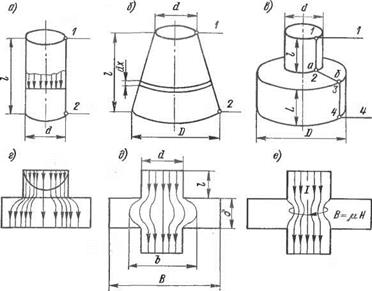
Цилиндрический стержень по рис. 1.21, а, нагруженный по­стоянным током, оказывает электрическое сопротивление между точками 1—2, точно соответствующее рассчитанному по формуле (1.67). Однако сопротивление конического стержня (рис. 1.21, б) надо определять, руководствуясь формулой (1.65). Если высоту всего (целого) конуса обозначить Д, то применительно к схеме, изображенной на рис. 1.2, б, можно записать равенство тангенсов:

D d

2Д 2 (А — I) ’

Сделав подстановку в формулу (1.66), сопротивление усеченного конуса можно определить:

і і

0

Рис. 1.21. Различные модели свариваемых деталей и распределение электрического тока по их сечению

Каждый из стержней рис. 1.21, в оказывает сопротивление: г і_2 = 4р//(ясР); г3_ 4 — 4р L/(nD2).

Однако общее сопротивление не будет равно их сумме:

Г1-2 + Г3-4 < ' ]_4-

Этот факт объясняется тем, что между точками 2—4 будут су­ществовать искривленные линии тока, а по плоскости перехода будет иметь место еще и эффект концентрации плотности тока по границе перехода (рис. 1.21, г). Искривление и концентрация соз­дают дополнительное сопротивление, что и отражает написанное выше неравенство.

Рис. 1.21, г и особенно рис. 1.21, д наглядно показывают, что геометрия детали и геометрия области распространения линий тока могут решительно отличаться друг от друга. Следовательно, электрическое сопротивление всякого проводящего участка надо определять не по геометрии этого проводника, а по геометрии пространства в нем, охватываемого линиями тока.

Так, в частности, размер В (рис. 1.21, д) может быть и очень большим, но это вовсе не значит, что линии тока будут растекаться на все пространство В. В действительности растекание линий тока всегда какое-то ограниченное (границы его характеризуются размером Ь). Дальше, в следующем параграфе, будет показано, что магнитное поле самого тока может вообще ограничить расте-

кание. Линии тока могут быть сжаты, как это показано на рис. 1.21. е.

Принимая во внимание рассмотренные принципы растекания тока в металле, можно вернуться к понятиям контактных сопро­тивлений. Теперь уже ясно, что, измеряя полное сопротивление стыкового контакта, мы учитываем все макро - и микроискривле­ния линий электрического тока и можем судить, насколько эта кривизна велика при ступенчатом изменении малого диаметра d на большой D.

Если металлические поверхности идеально очищены от оксид­ных пленок и если оказалось, что по контурному кругу диамет­ром d детали сварились, то сопротивление стыкового контакта по формуле (1.63) превратится в RKC = ггс.

В электротехнической литературе существуют методы расчета, по которым можно определить, что

ггс = Р (lid — 1 ID). (1.69)

Эта формула отвечает, как видно, физическому смыслу изме­нения величины ггс для любого значения р и любого размера d. Согласно формуле (1.8),

d = Df 1 - (1.70)

В то же время

р«р0(1 + а Г), (1.71)

а — температурный коэффициент сопротивления.

Подставляя в (1.69), получаем:

гге=£0^^_!__1у 0.72)

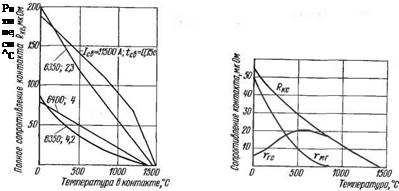
По этой формуле уже можно вычислять изменения величины ггс при изменении температуры. С другой стороны, изменение пол­ного сопротивления стыкового контакта от температуры можно установить экспериментально. Для этой цели снимают осцилло­граммы: UK = f (t); /св = f (t); Ти = f (t).

По зависимостям такого рода, показанным на рис. 1.22, можно считать, что полное сопротивление контакта в процессе сварки стержней диаметром 12 мм RKC падает от начального значения к нулевому линейно. Вычислим по формуле (1.72) изменение соот­ветствующей составляющей ггс. Вычитая из ординат Rrc ординаты ггс, получим достоверную кривую изменения гмг (рис. 1.23). Расчетным же путем получить эту зависимость весьма затрудни­тельно, так как расчеты, как было отмечено, окажутся связан­ными с целым рядом неопределенностей.

Рассмотрим эти вопросы подробно, используя принятую нами систему моделирования шероховатости в виде правильных пирамид 52

Рис. 1.23 Расчетно-графическое опре­деление составляющей по зависимо­стям, приведенным на рис. 1.22, и по формуле (1.72) (стыковое соединение стержней диаметром 1,2 см)

сопротивление металла пирамиды.

Формула (1.75) содержит, по крайней мере, три неопределен­ности: различные условия контактирования шероховатостей и неопределенность размеров пирамид (см. табл. 5 приложения).

Если все пирамиды по размерам условно считаем одинаковыми, то общее электрическое сопротивление контактирующих микро­пирамид таково:

Гит = (1 2) рдf/(nay). (1.76)

Поскольку пау = А„ то, используя формулу (1.15), находим: nay - па21/" 1 — е~х = Ас |/~ 1 — е“~х;

(I - н2)рА/

AcVl— е~Х '

Удельное сопротивление металла пирамид определяется [7 ] так: Рд = Ро [(1 + аТ) + ~ еР/°т ] , (1.78)

где р! ат — отношение давления, действующего на контурную площадь контакта, к пределу, текучести сильно наклепанного металла. Формула (1.78) показывает, что величина рд тоже вносит в расчет значительную неопределенность. Практически эта харак­теристика во много раз больше удельного сопротивления самого металла деталей: для металла, зачищенного наждачным кругом, — в десятки раз, для холодного проката — в тысячи раз.

Все неопределенности, содержащиеся в формуле (1.75), пока­зывают, что практические расчеты микрогеометрического внутрен­него сопротивления контакта по формуле (1.77) возможны только с помощью ЭВМ. Однако существующая технологическая практика пока что таких задач перед технологами не ставит. И тем не менее формулы такого типа, как (1.77), необходимо иметь в виду и технологу, поскольку формулы показывают достоверную теорети­ческую связь многих переменных, определяющих и поясняющих нестабильность начальных сопротивлений контакта.

Рассмотрим, как формула (1.77) отображает процесс дефор­мации пирамид шероховатости и тем самым процесс изменения их электрического сопротивления. При полном смятии пирамиды, т. е. превращении ее в параллелепипед, f = Д/3. Относительная деформация при этом, согласно определению (1.3), (1.4), f = = Д (1 — є), тогда є = 2/3.

Полное смятие всех пирамид дает следующий результат:

гМг = рдД(1-2)/(ЗЛс). (1.79)

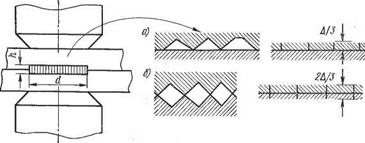
Эта формула относится к тому конечному моменту деформации пирамид, когда все они как геометрические фигуры исчезли и создали сплошной слой деформированного металла - толщиной от Д/3 до 2Д/3 (рис. 1.24, а и б). С этого момента в контакте двух деталей активным сопротивлением становится именно этот слой, а не группа контактирующих микропирамид.

Рис. 1.24. Схема деформации пирамид шероховатости при точечной сварке и формирование из них расплавленного диска высотой h = (1/3-ь2/3) А

S4

Изменение высоты пирамиды f в процессе ее деформации определяется так:

При X = 4 практически е~х -* 0; у 1 — е~х -> 1 и / = Д/3. Рассматривая деформацию пирамид как процесс ударного оса­живания, можно из равенства (1.32) определить для любой еди­ничной пирамиды

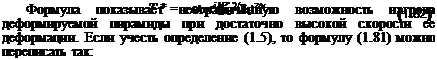Тд = re2l(6knt). (1.81)

Она показывает, как влияет характер шероховатости на темпе­ратурные вспышки в плоскости контакта при ударном сдавлива­нии деталей. До сих пор в технологии контактной сварки никто не принимает в расчет бесспорный факт возникновения вспы­шек температуры в плоскости контакта. Никакая точечная машина не прикладывает давление электродов медленно, статически. Дав­ления прикладываются безусловно и во всех случаях ударно. Отсюда практический вывод): наиболее достоверные измерения контактных сопротивлений получаются осциллографированием процесса сваривания точки непосредственно на точечной машине. Измерение контактных сопротивлений на каких-либо отдельных приборах при статических давлениях не соответствует реальной действительности.

Для контактной точечной сварки все понятия о полном сопро­тивлении контакта и его составляющих заметно усложняются по

сравнению с контактами стыковыми. Здесь требуются дополни­тельные пояснения, и притом достаточно подробные. Прежде всего уточним, что мы измеряем при точечной сварке, если речь идет о сварке деталей и шероховатых, и не свободных от оксидных наслоений. В этом общем случае полное сопротивление контакта можно записать равенством, аналогичным (1.64), но только с ин­дексом, указывающим на точечную сварку:

/?кт — гг

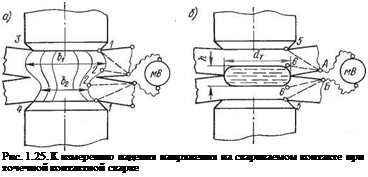
Для измерения вёличины /?ит к свариваемым деталям присое­диняем милливольтметр. Допустим, что присоединяем его к точкам А, Б (рис. 1.25, б). Как уже отмечалось ранее, сварочный ток, пронизывая детали, займет объем, представляющий собой неко­торую фигуру, очерченную линиями 1—1—3—4. На рис. 1.25, а показано, что линии тока могут растекаться на какое-то расстоя­ние (верхний лист), но могут и быть сжатыми. Так или иначе, но милливольтметр, присоединенный к точкам А, Б, будет снимать с токоведущей фигуры 1—1—3—4 некоторое падение напряжения не только с плоскости контакта, т. е. не только с точек 2—2, но и с точек 1—1, поскольку сам свариваемый металл — это тоже часть проводниковой цепи милливольтметра. Другими словами, милли­вольтметр на схеме 1.25, а реагирует на все искривления линий сварочного тока. Следовательно, он точно фиксирует всю сумму падения напряжения на составляющих, входящих в формулу (1.83), т. е. позволяет определить действительное значение RK4j. Для холодного контакта, т. е. в момент включения сварочного тока, эту величину можно- отмечать еще дополнительным нулевым ин­дексом /?кт0. Таким образом, видно, что применение милливольт­метра не позволяет измерить отдельно составляющую гмг. Мало того, она вообще не может быть отдельно измерена с помощью моделей вроде, например, набора шайбочек, поскольку любая мо­дель, отличающаяся от реальных свариваемых деталей, нарушает и геометричность, и деформационное подобие в самом контакте.

Рассмотрим теперь, что же измерит милливольтметр в момент формирования расплавленного ядра сварной точки (рис. 1.25, б). Как видно, и в этот момент от точек А и Б как бы идут измери­тельные провода А—5, Б—5, А—6 й Б—6. Поэтому прибор снова регистрирует усредненное значение падения напряжения на сва­риваемых деталях. Однако в этот момент оформления расплавлен­ного ядра между точками 6—6 оказывается включенным металл с удельным сопротивлением, характерным для точки плавления, которое много выше, чем у твердого металла. Следовательно, какие бы искривления линий электрического тока ни сохранялись в слоях 5—6, главным элементом сопротивления оказывается Слой 6—6, т. е. расплавленное ядро. Таким образом, в момент выключения тока полное сопротивление контакта превращается в сопротивление расплавленного ядра сварной точки, т. е.

Этот вывод проверен многолетней практикой и, таким образом, электрическое сопротивление ядра сварной точки в момент выклю­чения тока можно определить достаточно точно. Моделируя ядро как цилиндр диаметром dT и высотой h (см. рис. 1.25, б) и полагая удельное сопротивление соответствующим точке плавления ме­талла рт, можем написать:

гт = 4р Th/(nd?). (1.85)

Эта величина будет играть существенную роль в дальнейших технологических расчетах.

Обратимся теперь к типовым зависимостям RKT от времени при точечной сварке, одна из которых представлена на рис. 1.26. Для чистых металлических поверхностей эта зависимость пред­ставлена кривой 2, для поверхностей с заметным слоем оксидной пленки —1 кривой 1. В обоих этих случаях при правильном про­граммировании сварочного тока может быть получена сварная точка одного и того же размера, соответственно чему и конечное значение гт будет одинаковым.

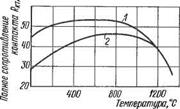
Построив по данным типовых осциллограмм зависимость RKT от температуры в плоскости контакта, получим типовую кривую, показанную на рис. 1.27 (для точечной сварки СтЗ толщиной 4 +4мм). Здесь вычисление составляющей ггт нельзя вести с такой же уверенностью, как это делалось для величины ггс при стыковой сварке. Размер области растекания Ьх (см. рис. 1.25, а) или Ь2 электрического тока в металле — величина переменная не только в зависимости от геометрических размеров, но й от физи­ческих свойств металла в данный момент. О величине ггт можно говорить только в общем виде. и с некоторым приближением. Однако снова можно повторить, что и это понятие весьма полезно не так

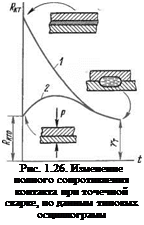для .расчетов, как для более пол­ного понимания физического смыс­ла протекания сварочного тока в свариваемых деталях.

Рнс. 1.27. Типовая кривая изменения полного сопротивления контакта при сварке стальных листов в зависимости от температуры, измеренной на краю ядра сварной точки: 1 — Гсв = 10 кА; 2 — /св = 14,5 кА

В результате можно сделать следующий вывод.

1. И экспериментальные, и расчетные определения значений электрических сопротивлений холодных контактов любой кон­струкции представляют собой весьма неопределенные характери­стики. Ориентироваться на них в технологических расчетах — это значит мириться с заведомыми, почти во всех случаях нетер­пимыми неточностями.

2. Ценность теоретических расчетных формул в том, что они показывают отчетливые взаимосвязи главных переменных, опре­деляющих не только статические состояния металлических свари­ваемых контактов, но и, самое главное, динамику контактирова­ния на всем протяжении процесса сваривания контакта.

3. Для точечной сварки все расчетные соображения по сва­риваемому контакту весьма рационально ориентировать на элек­трическое сопротивление контакта в момент выключения тока, что численно с достаточной точностью определяется электриче­ским сопротивлением расплавленного ядра, моделируемого как цилиндр диаметром dT и высотой h.

Вопросы нестабильности сопротивлений начальных холодных контактов еще раз будут рассмотрены в дальнейшем, когда речь пойдет о программировании режимов точечной сварки. Там же бу­дут рассмотрены и вопросы полярности контактных сопротивле­ний, а также характеристики электрических несвариваемых кон­тактов.