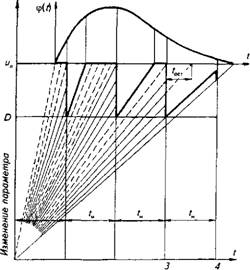
Динамика изменения параметра технического состояния со­вокупности одноименных составных частей агрегата характери­зуется «веером» реализаций, а рассеивание случайных величин их ресурсов - плотностью распределения ф(0 (см. рис. 9.8).

О 1 2 Ресурс составной части в единицах межконтрольной наработки Рис. 9.8. Реализация изменения параметра технического состояния одноименных составных частей с учетом /м и допускаемого отклонения D

В процессе эксплуатации через определенные наработки TM Составные части диагностируют и определяют потребность их в ремонте или в техническом обслуживании, если отклонение па­раметра технического состояния в момент контроля ui(tK)>D. При этом часть одноименных составных частей отказывает в процессе эксплуатации, если их ресурс оказался меньше наработ­ки до первого контроля, или остаточный ресурс оставленной для дальнейшей работы составной части меньше межконтрольной наработки TM (реализации изменения параметра таких составных частей изображены на рис. 9.8 штриховыми линиями). Ресурс отказывающих составных частей используется полностью. Ресурс

Остальных составных частей, которые заменяют, ремонтируют или обслуживают после контроля, если ux(tK)> D, недоиспользу­ется на различную величину T0CT (реализации изменения парамет­ров технического состояния таких составных частей изображены на рисунке сплошными линиями).

Изменение допускаемого отклонения параметра техническо­го состояния или межконтрольной наработки TM влияет на вероят­ность отказа составных частей Q(D0, TM) и их средний фактически используемый ресурс? ф(Дь tu), причем любое изменение Z)0, или TM улучшает один показатель Q(D0, TM) или T$(D0, TM) и одновре­менно ухудшает другой.

(9.23)

G(Dn) = Min U 0<0<i/„

Оптимальное допускаемое отклонение параметра техниче­ского состояния из условия обеспечения минимума удельных из­держек на эксплуатацию и ремонт при заданной межконтрольной наработке определяется минимумом функции суммарных удель­ных издержек

AQ(D0) + C[l

^ .Фф) гф(Я) J

При любом Д)<1 вероятность отказа (2(A)) < 1, а средний фактически используемый ресурс составной части t$(D0) < Тср. Вероятность отказа вычисляют по формуле

I-1 Dn

T ■L (

I-Tn

(9.24)

-Fr,

Где F0 - нормированная и центрированная функция нормального распре­деления случайной величины; I - порядковый номер межконтрольного периода, перед которым измеряют параметр технического состояния;

1

П.

1-А, Ст„ =-

(9.25)

(9.26)

Ор - среднеквадратическое отклонение ресурса составной части. Сред­ний фактически используемый ресурс составной части вычисляют по формуле

(9.27)

(А) = /i (А) + Л (А) + /з (А) где/1 (D0) вычисляют по формуле

1-1 А

- т

(i-T V сто J

Fx (Z)0) = r0g(Z)0)-a0Ј

; (9.28)

Фо

"Фо

/2 (D0) вычисляют по формуле

—— Т А °

(9.29)

V ст0 У

Л(А,) = 2>"

/j (D0) вычисляют по формуле

I-l А

Т

(9.30)

/з(А) =

-Я.

' I

А^

Где и2 вычисляют по формуле

= [2,5^3]-Т0,

О0 - индекс плотности вероятности нормированного и центрированного нормального распределения случайной величины.

Разность в квадратных скобках выражений (9.24), (9.29) и (9.30) всегда берется как положительная величина.

При степенной аппроксимирующей функции изменения пара­метра технического состояния вида u(t) = V'a в формулах (9.24), (9.25) и (9.27)-(9.30) вместо D0 применяют D^ а. Функции, приме­няемые при оптимизации периодичности регламентного обслужи­вания, а также обычные функции случайной непрерывной величи­ны технического ресурса, широко применяемые в теории надежно­сти, можно интерпретировать как частные случаи полученных вы­ражений. Для этого достаточно принять D0 = 0 и D0= 1.

Формулы (9.24)-(9,30) позволяют определять вероятность от­каза Q(DQ) и средний фактически используемый ресурс элемента /ф(Д)) для гладких функций изменения параметра. Если реализа­ции параметра имеют вид ломаных кривых (аг> 0(05), а межкон­трольная наработка Tu имеет значительное рассеивание, то реше­ние задачи резко усложняется. В этом случае применяют метод статистического моделирования случайных процессов на ЭВМ.

Оптимальное допускаемое отклонение параметра техниче­ского состояния и оптимальную межконтрольную наработку из условия обеспечения минимума суммарных удельных издержек на эксплуатацию и ремонт определяют по минимуму функции.

ОНУ.). Min И0"'-' + Ci' + "W-Ul, (9 31)

Где K(D0, /„) - число проверок составной части за период эксплуатации при установленных D0 и /"„.

Для построения номограммы, приведенной в ГОСТ 21571-76, многократно решают задачу отыскания значений D0 и tM. обеспе­чивающих минимум функции (9.31), при различных сочетаниях исходных данных Т0, v, а, А0, В0.

(9.32)

Оптимальное допускаемое отклонение параметра техниче­ского состояния из условия обеспечения максимальной безотказ­ности устанавливают с помощью целевой функции

Q(D0)-tM

?(Z)0)= min

0<D0<1

'Ф(А>)

Где Q(D0) - вероятность безотказной работы за межконтрольный период.

Так как с уменьшением Do величина Q(Do) уменьшается зна­чительно быстрее, чем t$(Do), то максимальная вероятность без­отказной работы составной части соответствует минимальному значению Q{D0), вычисленному по формуле (9.24).

При близком к нулю oz минимальное значение Q(Do) получа­ют в том случае, когда во втором межконтрольном периоде (/ = 2) QI{DQ) = 0, так как управлять безотказностью составной части с помощью Do возможно только, начиная со второй межконтроль­ной наработки (см. рис. 9.7). Вероятность отказа составной части
в период до первого контроля Qi зависит только от характеристик распределения ее ресурса и величины /м. Так как при 2г(А)) = О F0 в конце первого и второго межконтрольного периода будут одинаковы, то выражения в круглых скобках формулы (9.24) бу­дут равны между собой при / = 2,

2-Т D 0

—± = ------------------ (9.33)

Ст0 ст0

Или аналогично при степенной функции изменения параметра

_ у> гч1 'а о

±Zi°=ii>---------------- . (9.34)

Ст0

Из (9.34) находим условие, обеспечивающее максимальную вероятность безотказной работы составной части

А)=0,5а

Абсолютное допускаемое отклонение параметра техническо­го состояния при этом будет

D = 0,54-

Статистическим исследованием случайного процесса измене­ния параметра технического состояния при а:> 0,05 установлено, что максимальная вероятность безотказной работы наблюдается при

D = 0,3 аип.