Формулы для перевода показателей технического состояния, найденных при степенной функции изменения параметра в аналогичные показатели при применении других аппроксимирующих функций изменения параметра
 26 февраля, 2013
26 февраля, 2013  admin
admin Применение различных аппроксимирующих функций имеет наряду с известными преимуществами (повышение точности аппроксимации) серьезный недостаток. Каждая функция требует своих приемов вычисления, применения соответствующих формул, таблиц и номограмм, что резко усложняет процесс определения показателей.
В этой связи целесообразно после выбора и нахождения коэффициентов любого аппроксимирующего выражения преобра
зовать его в одну определенную функцию, для которой следует разработать таблицы и номограммы. Это единственный вариант для широкого применения класса аппроксимирующих выражений при относительно небольшом математическом и другом обеспечении определения показателей технического состояния. Естественно, что в качестве преобразованной функции желательно избрать линейную, как наиболее простую.
В таблице 9.4 приведены формулы для перевода аппроксимирующих функций в базовый вариант задачи допускаемого отклонения параметра технического состояния при а = 1, А/7 = 0. Чтобы возможно было ими пользоваться, следует провести соответствующую обработку исходных данных. Правила обработки следующие:
- определяют показатели изменения параметра А/7, ип, показатель а для степенной и показатель а для экспоненциальной функции;
|
'п |
|
|
|
Для экспоненциальной функции |
|
|
- нормируют и преобразовывают значения u(t) - А/7: для линейной функции
_ их (?) - А/7
Где ип = Пп - Пи| - Л/7; для степенной функции
- находят на основе полученных рядов D0I и T (T = 1, 2, . . ., п, где п - число составных частей) средний ресурс и коэффициент вариации ресурса при а = щ = 1;
- определяют D0Om в соответствии с требованиями, установленными выше;
- подставляют значения D0Om в формулы для определения оптимального допускаемого отклонения параметра технического состояния, приведенные в таблице 9.4, и вычисляют 7>0ОПТ. Для экспоненциальной функции изменения параметра
Ип=|Яп-Я„| + ЛЯ, а оптимальное допускаемое отклонение параметра
Nz ~ Пн ±(7)опт- Л/7).
|
Таблица 9.4 Формулы для перевода показателей, найденных при Применении степенной функции изменения параметра, в аналогичные показатели при использовании других аппроксимирующих функций изменения параметра
|

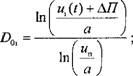
 Опубликовано в
Опубликовано в