При рассмотрении течения между двумя параллельными пластинами использу­ется то г же подход, что и в разделе 3.1. Для анализа принимается элементарный объем жидкости, имеющий форму прямоугольного параллелепипеда высотой dx, шириной В и длиной L (рис. 3.2), для которого уравнение равновесия сил преобразуется в дифференциальное уравнение, аналогичное уравнению (3.5):

Зт дх

Др L

(3.30)

а: -	Р(г)	т(х+ dx)	i P(z+dz)
	т(х)	о ><
	--------- d 2 -------- т

Рис. 3.2. Равновесие сил, действующих на элементарный объем жидкости при течении через щелевой канал

Важно иметь в виду предположение о том, что все величины в направлении оси координат, направленной параллельно ширине, остаются постоянными (т. е. краевым эффектом можно пренебречь, что эквивалентно предположению о бесконечной ши­рине канала). Проинтегрировав уравнение (3.30) и воспользовавшись граничным условием т = 0 приз: = 0, получим:

, , АР

*(*) - ■ X.

(3.31)

Как и в случае течения в канале круглого поперечного сечения это соотношение не зависит от характера течения.

Случай А — ньютоновская жидкость.

Предполагая, что расплав представляет собой ньютоновскую жидкость, имеем

dv

т=-г(3-32) ах

Подставляя уравнение (3.32) в уравнение (3.31), получаем

d Др

-п

В = - т— В - dx. (3.33)

dx L

Гн'2 V2 2

Интегрируя по координате х и учитывая граничные условия vz = 0 прих = - Я/ 2 и х = Я / 2, получаем выражение для распределения скоростей потока в щелевом ка­нале бесконечной ширины:

- х2

Ар

v2(*) =

(3.34)

2д1

Максимальная скорость течения наблюдается, когдах = 0:

(V2^ max о „г ' (3.35)

ApR?

1^1

Средняя скорость соответствует интегралу

Я/2

■И-

, ДрЯ2

(3.36) - Я/2

Сравнивая уравнения (3.35) и (3.36), получаем следующее соотношение макси­мальной и средней скоростей:

V - — (v) . (3.36.1)

2 з '.'Vinax. v '

Выражение для объемного расхода получается путем интегрирования по всему поперечному сечению

Я/2 В

^=J )vz(x)dydx. (337)

-Я/2 0

Здесь В — ширина канала. Уравнение (3.37) справедливо только при условии, что В »Я, иными словами, если краевыми эффектами можно пренебречь. На практике это уравнение обеспечивает удовлетворительную точность расчетов, когда В превы­шает Я в 10 и более раз.

Среднее время пребывания расплава в канале соответствует выражению

12riL2

(338)

Скорость сдвига на стенках получается на основании уравнений (3.31), (3.32) и (3.37):

(3.39)

ДpH 6V

гу

Сила сдвига, действующая по поверхности пластины, получается из уравнения

(3.31) . Результирующее соотношение имеет вид

(3.40)

Я

Fz = В ■ L - АР ’ в у-

Снова, как и ранее, уравнение (3.40) не зависит от характера течения.

Случай В — псевдопластическая жидкость, подчиняющаяся степенному закону течения.

(3.41)

В соответствии с определением степенного закона, заданным уравнением (2.5), выражение для напряжения сдвига приобретает вид

	т ( dvz'
	I dx,

SHAPE * MERGEFORMAT

'Г	т	(	dvz
			dx у

Комбинируя уравнения (3.31) и (3.41), получаем

(3.42)

Лт Ар

х.

После преобразования получаем выражение для скорости сдвига

т

(3.43)

Ар

dx

Проинтегрировав уравнение (3.43) с учетом граничного условия vz = 0 при х = Я / 2, получаем выражение для распределения скоростей по высоте щели:

/ + 1 Я | 2 V /

у-т + 1

г. т Ар

(3.44)

vz(x) = ф

т + 1

Аналогично уравнениям (3.35) и (3.36) получаем

(vz)max v;

(3.45) (3.46)

V, =

'Ар	т	'н
U J		2 /

J

2 т + 2

т + 1

z/max vz(x - 0) т + 1

f. т Г -т + 1 Ар

Соотношение между максимальной и средней скоростями получается путем де­ления (3.46) на (3.45):

V. то + 1

(3.47)

то + 2

(v2)n

Как уже было показано ранее, для ньютоновской жидкости (то = 1) это соотноше­ние составляет 2/3.

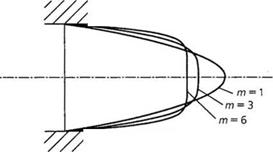
С увеличением то, то есть с ростом псевдопластичности, профиль скорости стано­вится все менее и менее заостренным (стержпеобразным) (рис. 3.3), максимальная скорость уменьшается, а соотношение скоростей приближается к 1.

V/////////Z, У7777777777, Рис. 3.3. Профили скоростей для различных значений индекса течения

Объемный расход получается путем интегрирования уравнения (3.44) по всему поперечному сечению:

Ф

(3.48)

У=

~>т + 1

VT В-1Г"+2

= й • Я ■ v.

т + 2

Среднее время пребывания получается из выражения (3.46):

21 Я

7Л + 1

(3.49)

то+2 2L

f” £/v

фДд"

Сила сдвига, действующая по поверхности пластин, так же, как и в уравнении (3.40), не зависит от характеристик потока. Как и в предыдущем случае, при то = 1 и г| = 1/ф уравнения переходят в уравнения, справедливые для ньютоновской жидкости.