При рассмотрении течения через кольцевой зазор можно использовать те же предположения и условия, как и при рассмотрении течения в канале круглого попе­речного сечения (см. раздел 3.1). Уравнение движения, приведенное в уравнении (3.1), в данном случае тоже приводит к уравнению (3.6) [1]:

Ар Сх

т(г)= —г+ —. w 2 L г

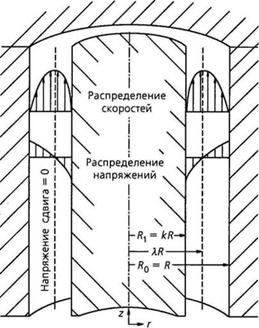
Чтобы решить уравнение (3.6) для данного случая, необходимо сделать предпо­ложение, что напряжение сдвига т принимает нулевое значение при г - Хг (рис. 3.4), где скорость v2 принимает максимальное значение ( v7)max. Внешний радиус кольцево­го зазора равен R.

Рис. 3.4. Течение через цилиндрический кольцевой зазор

Таким образом, С1 = - -^- (XR)2. На данном этапе значение X еще не известно. На основании уравнения (3.6) получаем

ApR 1Г

— - Х2 — R г

т (г)

(3.50)

Для течения ньютоновской жидкости скорость сдвига вычисляется по следую­щей формуле:

Проинтегрировав это уравнение, получаем

~	( 2	R	~
	г	- 2Х2 In	+ С2
	Я,		Я,

2 rL

A pR

(3.52)

V2(r) = -

Значения двух неизвестных величин X и С2 можно определить, используя следую­щие граничные условия:

• при г = kR, vz = 0;

• при г = R, Уг = 0.

Здесь k — соотношение внутреннего и внешнего радиусов кольцевого зазора, т. е.

(3.52.1)

*4-

Подставив граничные условия и соотношение (3.52.1) в уравнение (3.52), полу­чаем

1 -*2

2^2=-

hfp

С2 - -1. (3.52.2)

Таким образом, распределение скоростей можно выразить следующей форму­

лой:

l-*2

R2Ap ArL

ы -

1 -

v (Г) =

R, +

(3.53)

т* Ч*У

In

Когда г = X./?, получаем выражение для максимальной скорости потока (v ) :

1-k2

1 - In

(v2>n

(3.54)

2ln|-

2 In

R2Ap 4 rL

Средняя скорость получается путем интегрирования уравнения (3.53):

-kA 1 - fP -

R2Ap 4rL

(3.55)

v2 =

l-*2

V 4*7

In

Объемный расход V получают, умножая выражение для средней скорости на пло­щадь поперечного сечения кольцевого зазора:

(1 - k2)2

nR4 81

(I-*4)

V=*kR2( -&2) v,

(3.56)

■Др.

V л

In

К

Среднее время пребывания расплава в канале обратно пропорционально средней скорости:

-l

8r|L2 /?2Др

(3.57)

-k4 -k2

t = L/■ -

-k2 , (■ In

Выражения для сил сдвига Fz, действующих по стенкам кольцевого канала, имеют

вид:

общее— (Fz)total = tr = R-2nRL-ir„kR-2KkRL = nR2( - k2)Ap; (3.58а)

l-k2

(3.586)

T KkJ

для внутренней стенки — (Fz)inner = ~kR ' 2kkRL - ApnkR2

2k In

-k2

(3.58 c)

для наружной стенки — (F2)ou[er = tl. _ R ■ 2nRL = ДpnR2

2 In