{она дозирования одношнековых экструдеров является наибо - II •• изученной. Расчет производительности и мощности привода

• •'шошнсковых экструдеров производится в настоящее время на •и ионе анализа процессов, протекающих в зоне дозирования.

>ю объясняется тем, что в этой зоне применимы основные за-

• юн.! гидродинамики сплошных сред (уравнения неразрывности и ншжения). Зона же сжатия (пластикации), где осуществляется процесс перехода полимера из твердого состояния в жидкое, оста-

• и н наименее изученной, хотя она оказывает значительное влня­ни. па процесс экструзии и потребляет значительную часть мощ­но» in привода. Вероятно, этому можно найти объяснение в том, по перерабатываемый материал в этой зоне находится в переход - но. м состоянии (смесь расплава с твердыми частицами полимера), и и ном случае трудно говорить о применимости указанных выше

равнений. Задача усугубляется еще и тем, что в этой зоне имеет

место нестационарный тепловой процесс, а винтовой канал имеет переменные размеры сечений, вследствие чего доля расплава и смеси переменна подлине зоны сжатия. По этим причинам наи­большее число известных до сих пор исследований посвящено зоне дозирования. Дозирующая зона играет очень большую роль в одношнековом экструдере, так как обычно именно она он редел я - ет производительность машины.

В дозирующей зоне существуют три основных потока. Вынуж­денный поток (прямой поток) Оо представляет собой поступатель­ное течение расплава, которое возникает как следствие относи­тельного движения цилиндра и шнека. Противоток Qp, возникаю­щий под действием давления, развивающегося в формирующем инструменте, можно рассматривать как течение расплава в обрат­ном направлении. Третья разновидность потоков — это ноток утечки Оь в кольцевом зазоре между цилиндром и гребнем шнека. Перепад давления, возникающий вследствие существования по­вышенного давления в головке, между двумя боковыми поверхно­стями стенки канала вызывает появление утечки через кольцевой зазор между гребнем шнека и внутренней поверхностью корпуса.

Обычно утечка по сравнению с двумя другими упомянутыми выше потоками очень незначительна и ею в расчетах пренебрега­ют. Таким образом, производительность дозирующей зоны равна разности между расходом вынужденного потока и расходом про­тивотока и потока утечки:

(? = <?/>-(?,-&-

Вынужденный поток представляет собой поступательное тече­ние расплава, возникающее вследствие наличия вязкости у жид­кости и существования относительного движения шнека и цилин­дра. Если представить себе шнековую машину, на выходе из шнс-| ка которой расплав не встречает никакого сопротивления, т. с.| пакет сит и мундштук отсутствуют, то в этом случае давление в го­ловке будет равно нулю. Поэтому в канале шнека противоток не возникнет. Материал, находящийся в кольцевом пространстве между вращающейся наружной поверхностью сердечника шнека в внутренней поверхностью корпуса, подвергается сдвиговой де­формации. которая в результате воздействия боковых стенок вин­тового канала превращается в поступательное движение материа­ла по каналу, т. е. в вынужденный поток. Основными параметра­ми, определяющими величину объемного расхода вынужденного потока, являются глубина и ширина канала, диаметр шнека и ско­рость его вращения.

Противоток возникает в результате существования избыточно­го давления расплава в головке экструдера. Чтобы лучше понять причину появления противотока, представим, что шнек неподви­жен, а в головке машины имеется избыточное давление. В таком
» ivnae винтовой канал шнека уподобится длинной насадке примо - уюлыюго сечения. Тогда вследствие существования давления в m ювке расплав полимера потечет в обратном направлении вдоль типового канала. В действительности противоток представляет собой своеобразное ограничение вынужденного потока, численно равное производительности противотока, возникающего вслед - »|иие существования в винтовом канале градиента давления. Практически в канале шнека никогда не возникает потока в об­ратом направлении. На величину противотока влияют глубина винтового канала, длина зоны выдавливания, диаметр шнека, вяз­кость расплава и величина давления в головке.

Мри гидродинамическом анализе зоны дозирования одношнс - юных экструдеров (аналогия с винтовым насосом) используются i кмуюшие общепринятые предположения:

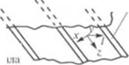
а) винтовой канал, образованный нарезкой шнека и стенкой цилиндра, рассматривается развернутым в плоскость (плоская за­йма);

б) считают, что шнек неподвижен, а цилиндр движется со ско - |нк гью Ус в направлении, перпендикулярном оси шнека (для оп - |к дсления положения частицы жидкости но отношению к шнеку);

в) массовыми силами можно принебречь;

О жидкость заполняет винтовой канал полностью и прилипает к стенкам (к поверхностям шнека и цилиндра);

О жидкость несжимаема, и температура ее одинаков;! по всему оо|,сму (изотсрмичность процесса);

е) рассматривается прямоугольный профиль винтового канала < постоянными размерами по длине, т. е. поперечное сечение ка­па за не является функцией координаты г;

ж) ширина винтового канала Wнамного больше его глубины /?,

I с. W >> /; (рис. 2.29);

^ Ось шнека

О учитываются только поперечная у, и продольная v. компо­ненты скорости — предполагается, что вертикальная составляю­щая vy скорости жидкости не оказывает существен­ною влияния на процесс »кеГрузии, т. е.

I - Ом " NN V M

Рис. 2.29. Плоская модель зоны кхнропамня одношнскового экструдера

N у /PiHllCpTKd 44 c* шнека

V* » vr, V-. » vr

I 1овсрхность корпуса Стенка канн

Из последнего допу­щения следует, что в расчетах рассматривают - «я только компоненты вектора скорости v* и vr I е ш предположить, что • идкость несжимаема,

•но ноток установивший-

ся и что вязкость постоянна, и если не принимать в расчет члены, выражающие ускорение, то компоненты х и z уравнения количе­ства движения примут вид (для каналов, у которых W » /;):

1 др d2v

-47 = —(2.60) И dz Ъу1

(2.61)

1 dp d2vx й dx ду2 '

где др/dz и Ър/Ъх — градиенты давления в направлениях осей гиг, v., vr — скоро­сти частиц жидкости а направлениях осей z и х.

Двойным интегрированием уравнения (2.60) получим следую­щее выражение:

^’Шт+С^ <2-62>

Постоянные интегрирования С и С2 выражения (2.62) нахо­дятся из следующих граничных условий, вытекающих из пред­положения прилипасмости жидкости к стенкам винтового ка­нала:

у= 0, vz =0;

у = h, V. = Vcz,

где У<; - компонента вектора скорости стенки цилиндра в направлении оси z-

При подстановке граничных условий в уравнение (2.62) полу­чим:

С2= 0;

с (2.63)

И ц dz 2

Тогда из уравнения (2.62) следует:

<264>

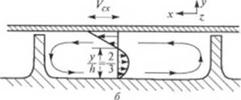
Первый член правой части уравнения (2.64) описывает ско­рость частиц вынужденного (прямою) потока v# жидкости, обус­ловленного относительным движением поверхностей цилиндра и шнека, а второй член — скорость потока под давлением (противо­тока) v-р, обусловленного наличием сопротивления головки (фор­мующего инструмента) (рис. 2.30, а).

v 0*8 — Вынуж - , -=2-0,6 — ленный

Противоток

8‘f ~lw, OK

0.0

■*4 Сердечник шнека

x'—^z

IVjy. H.liip)K)UIHH mm»K

1.0 у 0.8 — V0.6- ^3:1: 0.0

TT

<p = 0 9*1/3 9 — 2/3 9 = I Свободный Закрытый выход _ выход Рис. 2.30. Эпюры скоростей потока я тоне дотирования од - HOIHHCKOBOIO экструдера:

а - вдоль шипового канала; б - поперек вшпооого канала

(2.65)

Решение уравнения (2.61) при граничных условиях у = 0, у, = 0;

сх

у = И, Vjf = Vc

Оде Усх — компонента вектора скорости стенки цилиндра Vc в на­правлении оси х) записывается в виде:

v*=-*4-il(>,A->2)- <266)

И последнем уравнении первый член правой части описывает • трость вынужденного потока жидкости, обусловленного нали­чием Ум стенки, а второй член — скорость потока под давлением и I та наличия градиента давления др/дх (рис. 2.30, б).

Появление компоненты скорости vx объясняется наличием по­перечной циркуляции жидкости в винтовом канале шнека, обус- п'пленной толкающим действием боковых стенок винтового ка - M. I in. Следовательно, если пренебречь утечками через радиальный
зазор, величина которых обычно очень мала, суммарное значение расхода для течения в поперечном направлении будет равно нулю, так как с обеих сторон поток ограничен стенками канала. Поэтому

А

Rdy-0. (2.67)

о

Градиент давления Эр/Ох по направлению х находят подстанов­кой vx (уравнение (2.66)| в уравнение (2.67) и интегрированием получающегося при этом выражения. В результате можно легко убедиться, что

(2.68)

др_ 6уУсх

Э* /,2

Подстановкой этого значения др/дх в уравнение (2.66) оконча­тельно получим:

(2.69)

h [ И

Объемный расход жидкости Q можно получить интегрировани­ем компоненты v. вектора скорости жидкости по поперечному се­чению канала, перпендикулярному оси z. Математически это вы­разится уравнением: f

Q = Wvzdy. (2.70)

о

Совместным решением уравнений (2.64) и (2.70) окончательно получим:

<2-7»

Первый член правой части уравнения (2.71) является расходом прямого (вынужденного) потока, обусловленного относительным движением поверхностей шнека и цилиндра, а второй член — рас­ходом потока под давлением, появляющегося из-за наличия со­противления экструзионной головки. Преобразуем некоторые пе­ременные последнего уравнения при помощи следующих соотно­шений (см. рис. 2.29):

Vcz = Vc cosa = nD/Vcosa;

Тогда с учетом соотношений (2.72) уравнение (2.71) приводит ся к следующему виду:

п2 D2 sinacoso

>.N

---/г sin а я/)х

2

(2.73)

i. ic u„ (I — коэффициенты прямого и обратного патокой; /, h, W — шаг. глубина и ширима винтового канала; D — наружный диаметр шнека; /' — число заходов вин - 1о1юИ нарезки шнека; L — длина зоны дозирования шнека; a — угол подъема внн - Ю1ЮЙ нарезки; .V — скорость вращения шнека; Д/> — падение давления на длине юны дозирования шнека.

Первый член правой части уравнения (2.73) представляет собой производительность вынужденного потока Qd. а второй член — производительность потока иод давлением Qp. Видно, что QD за­висит только от геометрических параметров и частоты вращения шнека N, а поток под давлением — от свойств перерабатываемого материала и технологических режимов экструзии.

Кроме того, в зоне дозирования одношнековых машин суше - « гвуют утечки через кольцевой зазор между гребнем шнека и внут­ренней поверхностью цилиндра. Однако ввиду малости ими пре­небрегают.

Если уравнение (2.71) записать в виде

(2.74)

Q fr р Qd 6iVczdz

I де

(2.75)

/г i)p Ф 6цКс. Эг'

н» с учетом того, что

югко доказать, что

Q = QD-Qp,

(2.76)

v-Qp/Qp.

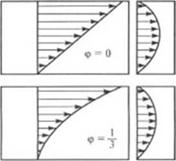
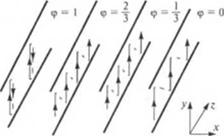
Коэффициент ф называют коэффициентом дросселирования. Величина ф оказывает большое влияние на распределение про­филя скоростей V. (рис. 2.30, а).

Аналогичным*" образом можно преобразовать и уравнение < ' 04), обозначив при этом через а отношение у/И, т. е. a —y/h. Тогда получим:

(2.77)

А - = а(1-Зф+Злф).

Легко убедиться, что ф имеет максимальное значение при мак­симальном градиенте давления (максимальный градиент давления получают в том случае, если выходное отверстие формующего ин­струмента закрыто). Так как в этом случае продольное перемеще­ние жидкости по винтовому каналу отсутствует, то можно предпо­ложить, что

I

jvzda=0. (2.78)

о

Если теперь подставить уравнение (2.77) в последний интеграл, то получим выражение, которое показывает, что максимальное значение ф равно единице (только при ф = 1 имеет место равен­ство нулю левой и правой частей приводимого выражения):

1-|<р+Ф = 0. (2.79)

Т

2

7

В ч

2 7

VJV,

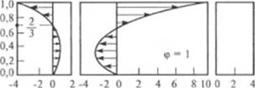
Рис. 2.31. Профили относительных скоростей потока в тоне дотирования:

V«/P«- моль типового канала; v,/Рс, - поперек винтового канала; ^/Ис - влоль оси шнека

в

УК,

о

Уравнение (2.69) можно 1лкжс записать в эквива - ichthoh уравнению (2.77) форме:

Рис. 2.32. Продольная циркуляция жидкости в винтовом канале

vx^cx =я(2-3я). (2.80)

Следует заметить, что если компонента скорости г. зависит от параметра пе­реработки ф и а = y/h |рис.

2.31 и уравнение (2.77)), то скорость vx зависит только от безразмерной перемен­ной а = y/h и не зависит от параметра ф (коэффициента дроссели­рования). Кроме того, координата ylv,=o = 2Л/3 не изменяется. Профили компонент скоростей потока для различных значений ф представлены на рис. 2.31.

Из рисунка видно, что при всех режимах работы (значениях ф) координата точки, где vx = 0, остается неизменной и равна а = 2/3, а координата точки, где v. =0, меняется в зависимости от величи­ны параметра ф. Следует заметить, что из-за наличия градиента ынления dp/dz в винтовом канале одношнекового экструдера на­ряду с поперечной циркуляцией имеет место и продольная цирку­ляция жидкости (рис. 2.32).