Анализ формул для расчета объемного расхода V, полученных в разделах 3.1 -3.3, показывает, что все они могут быть записаны в обобщенной форме.

(3.59)

Ар.

V=—Aр-^г т| Wr|

Здесь К — так называемая гидравлическая пропускная способность головки (die conductance), а№'=1 /К — гидравлическое сопротивление головки. Оба этих коэф­фициента зависят от геометрической формы канала экструзионной головки.

Обобщенная форма уравнения объемного расхода для ньютоновских жидкостей:

Обобщенная форма уравнения объемного расхода для псевдонластичных жид­костей

Применив степенной закон Оствальда-де Виля, сформулированный в уравнении (2.5), уравнение для объемного расхода можно переписать в виде

(3.60)

Здесь К — гидравлическая проводимость головки применительно к степенному закону, a G — обратная величина, известная как постоянная головки (die constant). Последняя используется в альтернативных формах уравнения объемного расхода, реже применяемых на практике. Обе эти величины являются функциями геометрии канала экструзионной головки и индекса течения т.

Уравнения (3.59) и (3.60) могут рассматриваться как основополагающие уравне­ния, описывающие течение в каналах экструзионных головок. Значения коэффици­ентов К и К для экструзионных головок с каналами простых геометрических форм, таких как круглой, кольцевой, прямоугольной (базовая геометрия), и с сечением лю­бой произвольной формы и суживающихся (конусных, клиновых) каналов (рис. 3.5) приведены в табл. 3.1 (см. также работы [4,5,9-19]).

Перепад давления Др • >

-L -

■L -

Перепад давления Др Щелевой канал (прямоугольная щель)

Перепад давления Др

Канал с поперечным сечением произ­вольной формы

Перепад давления др

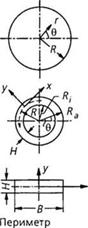
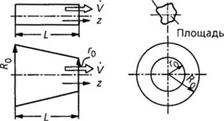
Рис. 3.5. Геометрические параметры основных типов каналов экструзионных головок

Конический канал

Канал с кольцевым поперечным сечением

Канал круглого поперечного сечения

Таблица 3.1. Значения пропускной способности головок К и Я*

Ньютоновская жидкость, t = ivy

Псевдопластичная жидкость, т 1 • tm = _.y

лЯ4 *=1Г (L/R>>V 2 лЯ + Я

Цилиндрическая труба (канал с круглым по­перечным сечением) Кольцевая щель

К'■

2 т(т + 3)

л(Я„ + Я()(Яя - Я,-)"

Я3 (Я/Я >0,1) к'■

К-

12 L

2га + 1(т + 2) лДЯ™ + 2 (1 I

(с поправкой на вход) . лКЯ3 К~ 6L

2т ’(т + 2)

nDH3 12 L

(Я/Я >0,1)

Я = -

(рассматривается как щель)

(1 - А2)2 1

л Я4

(1-А4)-

К-

, 1п(т)

8Z.

(k-R,/Ra) В Я4

ВИт + 2 flT r-2^T2)[lJ <В/Я>20>

я = -

(В »Я)

Прямоугольная щель

12L

для В / Я < 20 вводится по­правочный коэффициент / [111] (см. рис. 3.6)

А -

lr0 J

Я =

Я'

Конический канал

т • L	1 -	/ !±	з_" т
		1Л>;

Гг I3 го l«oJ

8L

2'n(m + 3)

а) В Я3 *~ЙГЛ

Канал с поперечным сечением произволь­ной формы

Значение / см. на рис. 3.6

т + 2

Л3

2Л

Я' = (m + 3)L - U (приближенная формула)

Я-

2LU2 (приближенная формула)

Здесь, как и в предыдущих случаях, необходимо напомнить, что все приведенные в табл. 3.1 соотношения получены на основе следующих допущений:

1. Течение изотермическое. Это означает, что все частицы расплава имеют одина­ковую температуру, а у стенок канала экструзионной головки такая же температура, как и расплава, т. е. теплообмен между расплавом и стенками канала отсутствует. Как правило, это допущение с приемлемой степенью точности можно считать справедли­вым для установившегося процесса экструзии.

2. Течение стационарное, т. е. профиль скоростей потока не изменяется с течени­ем времени. Данное условие справедливо для установившегося процесса экструзии.

3. Течение ламинарное. Это означает, что значения числа Рейнольдса, определяе­мого формулой Re “ 2 • г - v • р/ г), не превышают 2100 (условие справедливо практи­чески для всех полимерных расплавов).

4. Жидкость несжимаема (плотность расплава остается постоянной). Это допу­щение приблизительно соблюдается для полимерных расплавов при давлениях, раз­виваемых в типовых экструзионных процессах (см. раздел 2.2.1).

5. Влиянием эффектов на входе в канал и выходе из него можно пренебречь. Как правило, это допущение применимо, поскольку для ньютоновских жидкостей рас­стояние Le (так называемое гидродинамическое расстояние формирования ламинар­ного течения), необходимое для образования параболического профиля скоростей, определяется формулой [20]

Le = 0,035 • D • Re.

Как показано в работе [21], для полимерных расплавов это расстояние обычно меньше, чем радиус канала R. Этот же факт подтверждается и результатами числен­ного моделирования процесса течения, приведенными в работе [22].

При течении вязкоупругих жидкостей для формирования профиля скоростей требуется дополнительное реологическое расстояние, поскольку для них характерен так называемый эффект «памяти», связанный с тем, что материал «помнит» все пред­шествующие деформации. Для полимерных расплавов это расстояние больше, чем гидродинамическое расстояние для вязких ньютоновских жидкостей [23]. Его вели­чина зависит от реологических свойств расплава и в явном виде не может быть опре­делена простыми методами.

6. Скольжение расплава на стенке отсутствует. Для большинства полимерных расплавов это условие справедливо. Исключения возможны только для течения рас­плавов полиэтилена при высоких скоростях сдвига [24,25], некоторых композиций жесткого ПВХ, и, как правило, композиций на основе каучука [26]. Для этих матери­алов возможны конечные значения скорости скольжения на стенках (см. раздел 3.5).

Связь между напряжениями сдвига, скоростями сдвига [4,10,27,28], скоростями течения [1,4,29-31] и потерями давления [32] приведена в табл. 3.2-3.5. Эти зависи­мости получены на основе вышеприведенных допущений и упрощений в пределах их применимости.

Таблица 3.2. Напряжения сдвига т и напряжения сдвига на стенке Тц, для каналов с раз­личной геометрией поперечного сечения

Ар т г, 2L ДР L Х'

Ар ТцГ - R № 2L Ар тщ =—Я; н 2L г -k2 R R ~

Труба круглого по­перечного сечения Кольцевая щель

w R 2х 'Х*1Г Ь.

R Ар

2 In Ар

2х lw 11

Ар т “ х, L

Прямоугольная щель

2L ДрЛ UL

Канал с поперечным сечением произвольной формы

1иг-

Таблица 33. Скорости сдвига у и скорости сдвига на стенках канала уц,

Ньютоновская жидкость, т = л - у

Псевдопластичная жидкость, 1

Геометрия канала

4v. - г AV ■ г

Труба (канал с круглым поперечным сечением)

у - (т + 3) — R

у —

R2 nR* 4. у

(m + 3)V лй3

lw'

lw'

6- V ixDlfi ’ 6- V

2(m + 2)-V лDffi 2(m + 2)V л(Я„ + Rt)(Ra - P,)2

Кольцевая щель

Yiy‘

n(Ra + Ri)(Ra-Ri)2

6- V BH2

2v,(2x y-(m + 2)~ —

Прямоугольная щель

Yiy'

2(m + 2) • V BH2

Yiy'

Окончание табл. 3.3

Псевдопластичная жидкость, 1

Ньютоновская жидкость, т = л • у

Конический канал

Канал с поперечным сечением произвольной формы

а)

2 ■ V ■ U

Ь) 4 • V (приближенная формула)

Таблица 3.4. Скорости vz, средние скорости г, и максимальные скорости (vz)n

Псевдопластичная жидкость, 1

Ньютоновская жидкость, т = Л ' У

Геометрия канала

Труба (канал с круглым ДрЯ2	-	Гг)	2-		/ * I дя 1
поперечным сечением) v2 _ 4^	1 -	Я ч /		; vz= ф	к)

	Г (г)	2-		-	V	т + 1'
уг ” (v*)max			; v = (V ) • г ' г'max	1 -	я

т + 1

ApR2

г/max щ ’

(уг),пах “ Ф

/Дpm Rm + 1

(v/> ApR2 SrpL

Ф
т + 3	W

2L 4 /

m + 1 1 Rm + i;

: <vaW “ 2*г

M2

ApR2 V/“ 1цГ~ 1 -*2 Тт In

Кольцевая щель

1 -

,3 я.

ApR2 j Г 1 - k2 (vz)max " 4ni j1 “ [21п(1Д)у

-k2

1 - In

ApR2 ( 1 - k4 1 - A2 8r>L |^1 - k2 1п(1Д)^

Окончание табл. 3.4

Ньютоновская жидкость, т = ч - у

Псевдоплэстичная жидкость,

тт=4--Т

Прямоугольная щель

-Др] К2) L J т + 1

(VA,

гЪдт + 1

1 -

//, v у

Др//2

, ,я*1 Н

иф ' (vz)max”'3

1 -	(2х'	2-		Iй)
Н У	.	1 h ?	Л,

ДpH2 ~w

Др//2 8r>L ’

VT= (vz)n

'Ар'

2)

(vz)max Ф

т + ' т + 1

L

(н_ 2

г т + 2

Поправочные коэффициенты/;,(см. рис. 3.6) [7,8], применяемые к течениям нью­тоновских жидкостей через каналы прямоугольной или неправильной формы, были введены в табл. 3.1. Эти коэффициенты учитывают влияние отношения площади поверхности контакта с расплавом полимера (боковой поверхности) к площади по­перечного сечения канала (см. также [17,18]).

Если канал экструзионной головки представляет собой комбинацию участков простой формы, которые рассмотрены выше (а в большинстве случаев это именно так), то для получения суммарной потери давления по длине головки вычисляют потери давления на каждом из участков, а затем их суммируют. Этот же метод при­меняется и при расчетах сужающихся и расширяющихся каналов. В этом случае ка­нал разделяется на ступени (ступенчатая аппроксимация), в пределах которых форма поперечного сечения может считаться приблизительно постоянной (рис. 3.7). Затем подсчитывают потери давления на каждой ступени и определяют общий перепад дав­ления суммированием локальных перепадов давления по ступеням. Оценочные рас­четы потерь давления с погрешностью в пределах 10-30 % можно также производить с помощью уравнений и таблиц, приведенных в работе [19].

Потери давления для течения ньютоновских жидкостей через кольцевые каналы с эксцентриситетом и каналы ромбовидной формы могут вычисляться с использова­нием методов, описанных в работе [5]. Течение ньютоновских жидкостей через эл­липтические и эллиптически сужающиеся каналы описаны в работах [5,28]. Гидрав­лические сопротивления экструзионных головок для конических каналов описаны в работах [5, 27, 28, 32-35]. Однако формулы для расчетов применимы только для

оо

Таблица 3.5. Потери давления Ар / L в каналах с различной геометрической формой поперечного сечения

Ньютоновская жидкость, т = П • у

Псевдопластичная жидкость, 1

Псевдопластичная жидкость (при использовании характерных величин )

Др L

Ар L

R2

L	nDH3 '
Ар	12ц ■ V
L	ВН3
Ар	12ц • V

Прямоугольная щель

Ар 12т| • V

Н « D

L В-Я3-//

Ар L

Кольцевая щель

+ 2

ЭКСТРУЗИОННЫЕ ГОЛОВКИ ДЛЯ ПЛАСТМАСС И РЕЗИНЫ

l-k2)

R =Ra 6p _ L

Ap L

в»н

+ 2

В/Н< 20

а)

Ap L

Ь)

Ар L

(приближенная формула)

Труба круглого попе­речного сечения

Поперечное сечение произвольной формы

L В - Н3 - fp’ fp см. на рис. 3.6

fp см. на рис. 3.6

12 U2 ■ V ~73

Ар 12ц • V

8ц ■ V nR1

2фAm~2 (приближенная формула)

фnRm + 3 2т + 1 (т + 2) ■ V

(rn + 3)Um + 1- V

2m + ,(m + 2)V

2т (т + 3) • V

флОТ7"

фВЯ7"

Ар 8ц • V 8ц • у 8г| - L nR* nR 12rj ■ V

Универсально-применимой формулы для ц не существует

AP_______________ L n(,R2-I^)-R2

Ini 12rj • V 12ц • v

nDH3 8rj • V

1 + k2 +

Ар L

BH3

R„

0,9

0,7

0,3

_L

_1_

Узкая щель

. 1 Др ВН3 1 V=-——f^K-Apfp или др:

Др — перепад давления

Прямоугольник ^----------------

По Сквайрсу (Squires)

Квадрат (ip = 0,4217)

1,0

12 rVL ВН3

— вязкость — объемный расход — длина канала — коэффициент течения — наибольший из размеров поперечного сечения — наименьший из размеров поперечного сечения

0,8

0,6

=г I °-5 о V 0,4

Круг {fp= 12л / 128)

0,2

0 0,2 0,4 0,6 0,8 1,0

Коэффициент формы (форм-фактор Н/В)

Рис. 3.6. Поправочный коэффициент течения в зависимости от форм-фактора для каналов с различной формой поперечного сечения

Рис. 3.7. Ступенчатая аппроксимация канала с переменным поперечным сечением

ньютоновских жидкостей. Течение в каналах с треугольным поперечным сечением рассматривается в работах [18,36].

Часто вычислить потери давления в канале с поперечным сечением сложной кон­фигурации возможно путем разделения поперечного сечения канала на отдельные подобласти, для которых используют формулы для расчета течения в круглой трубе, радиус которой соответствует эквивалентной величине R, определяемой через бо­ковую поверхность и площадь поперечного сечения (аналог гидравлического диамет­ра). Значения этого радиуса для каналов с поперечным сечением произвольной фор­мы приведены в табл. 3.3 [10]. Результаты расчетов при такой замене являются лишь приближенными.

Таблица 3.6. Характерная скорость сдвига

Геометрия поперечного Псевдоплэстическая жидкость: характерные величины

_ 4V У ” ео: ео * 0.815

сечения канала

Труба с круглым поперечным сечением

V

(Я* - Я?)Я R 1

Кольцевая щель

1-А2

1+£2 +

lnfc

■ ё ■ 0.772

GV

Прямоугольная щель Значения е0 и е0действительны для 2 < т < 4 (см. рис. 2.16)

Расчеты с использованием концепции характерной вязкости

Расчетные формулы для нсевдопластичных материалов, приведенные в табл. 3.1-3.5, при использовании степенного закона становятся громоздкими. Для уравне­ний Прандтля-Эйринга или Карро это неудобство становится еще более очевидным. Однако уравнения, выведенные для ньютоновских жидкостей, намного проще. По этой причине удобнее использовать метод характерной вязкости, описанный в раз­деле 2.1.2. Этот метод позволяет применять уравнения для ньютоновских жидко­стей применительно к псевдопластичным материалам путем введения характерных величин.

Если известна некоторая характерная точка в канале (рис. 2.15), то, используя данный метод, для этой точки можно вычислить характерную (или эффективную) скорость сдвига у (см. табл. 3.6) на основе объемного расхода V и характерной вязко­сти г| для известной кривой вязкости. Затем полученное значение следует подставить в уравнения, полученные для ньютоновских жидкостей, и определить перепад давле­ния (см. табл. 3.5). Таким образом, можно получить простое уравнение течения через
экструзионную головку, аналогичное уравнениям (3.59) и (3.60), но использующее характерные параметры:

V-^-Ap. (3.61)

Значения гидравлической пропускной способности экструзионной головки при­ведены в табл. 3.1.

Эту процедуру следует применять как можно чаще, поскольку она очень проста.