3.1. Экспериментальное определение

R, L, С-параметров конденсаторной машины

Активное сопротивление R сварочного контура импуль­су сварочного тока, индуктивность L контура и емкость С батареи конденсаторов, а также коэффициент трансфор­мации п и напряжение Uco являются важнейшими пара­метрами, определяющими технологические возможности КМ. Знание этих параметров необходимо при расчете раз­личных элементов силовой части, в том числе сварочного трансформатора, тиристоров, а также при проверке этих параметров в эксплуатации. Для определения индуктив­ности и активного сопротивления КМ существуют различ­ные методы. Один из них — опыт короткого замыкания сва­рочного контура, проведенный при пониженном питающем сварочный трансформатор напряжении частотой 50 Гц, после чего активное сопротивление пересчитывается с уче­том частоты, эквивалентной импульсу сварочного тока. Другой — отыскание параметров контура по декременту колебаний. Для этого снимается осциллограмма тока раз­ряда, по ней определяется декремент затуханий и произ­водятся соответствующие вычисления. Вычисления полу­чаются проще, а результаты более точными, когда форму­лы процессов, происходящих в цепи разряда, выражаются в функции параметра р[12]. В этом случае можно легко определять R, L, С-параметры даже в случае апериодиче­ского разряда.

Для контура разряда КМ справедливо дифференциаль­ное уравнение

^+*£+^‘-=0. (3-І)

Приведем его решение при различных соотношениях d—R/(2L) и ш„= 1IVLC:

при 6<Cio0 (колебательный разряд)

i=^e~ltsnwt — I9e~bt -^-sinotf; (3.2)

при б=ыо (предельный случай апериодического раз­ряда)

при 6>coo (апериодический разряд)

е~Ъ* (g1^2-“ ° * £ — V&«—шг0 t J _

Uco

2L Кб2—со2

В этих формулах Uco — напряжение, до которого были заряжены конденсаторы перед разрядом, В; 6=R/ (2L)— коэффициент затухания контура, с-1; cn0= ’VLC — угло­вая частота колебаний тока в цепи при отсутствии в ней активного сопротивления (/?=0), с-1; ш = |Лог0 —S2—угло- вая частота собственных затухающих колебаний, с-1; 1Ш— ^со VC/L — амплитудное значение тока в цепи с

R—0, А. Введем параметр р:

р = 8/«, = R VCH. J2 = R/J(2UCo) = R'(2R0). (3.5)

где Rt = UcolL/C — волновое сопротивление, Ом.

Обозначим через В отношение текущего времени t к чет­верти периода То в случае R=0, т. е.

В = 4//Т, = 4Ао0/(2и) = 2f/(* ]/LC). (3.6)

Произведем преобразования:

рт. В

Учитывая (3.5) —(3.7), выразим (3.2) — (3.4) через па­раметр р:

при б<Ыо(р>»1)

. / вхр (— пВр, 2) . „bVI — p*

1 — у»----------------- sin------ о——

при 6=(Оо {р= 1)

exp ; (3-9)

при 6>ыо(р>1)

i=I.-^=f^-Sh^±7tByp‘~ 1). (3.10>

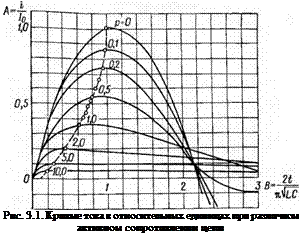Если теперь выражения (3.8) — (ЗЛО) поделить на ам­плитуду тока /0> то получится зависимость отношения Л = — і/’о от В. Эта зависимость при различных значениях р

представлена на рис. 3.1. Разделим равенства (3.8) —-(3.10) на /0, возьмем производную по В и приравняем ее нулю. Тогда для случая б<соо(р<1) получим

dA *Р ехР (— пВРІ2) • яВ V — р2 ,

ж-— ид—5—+

cos гіГІН2=о.

и, подставляя (3.11) в (3.8), определяем

. 1 — р arcsin Vзр

Л = - j - = exp-------- у . ------------- —

Л> к уТ—р2

Примем р->0 и найдем

г> , - 2 arcsin У1 — р2 ,

В = lim-------- у - = 1;

р~*0 п V - р2

А = lim exp (----- р arcsin У1 — р2) = 1.

Гі-Р* у 1

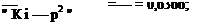При р-*-1 из (3.11) и (3.12) получим В= lim

р-* і

Л —lim exp (—^7^—р ■ arcsin Vа 1 — = е_1 = 0,3679.

р-* V1 — р2 ]

Для случая 6>шо(р>1) находим

ш-—пР2]В^Ь{пВр'2) 1ехр {жВ ^^гт/2) -

- ехр (- *в + ex2P|,pg 21х

А = 4- = {р + Ург-1) *0 Для р-*-оо имеем B==lim! lMp±£ElL_0; Р-*СО я VР2 — 1

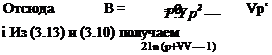—1 ехр (я/J l^p2— 1 2) ( тгУр2 — 1 ехр (я7?У^р2 — 1/2) |_________

А = lim (р - f - У~У~-І) ^!_l=0.

р-+ СО

Таким образом, можно построить таблицу значений А и В в зависимости от параметра р. При р—0 значения В —

— 1, Л=1; при 0<р<1 величина В вычисляется по (3.11), А — по (3.12); при р=1 имеем В=2/п=0,6366, А = 1/е= =0,3679; при 1<С/?<оо величина В вычисляется по (3.13), Л-по (3.14).

В табл. 3.1 приведены расчетные значения Л и В, а также их произведение в зависимости от параметра р. По­данным табл. 3.1 и экспериментально снятой кривой тока (по его амплитудному значению и времени до амплитуды) можно легко определить параметры RLC-u, eim.

Таблица 3.1

р	А	В	/4 в	Р	А	В	АВ
0	і	1	1	1,45	0,2821	0,5555	0,1567
0,05	0,9: 67	0,9693	0,8983	1,50	0,2749	0,5480	0,1506
0,10	0,8626	0,9409	0,8116	1,55	0,2681	0,5407	0,1450
0,15	0.8062	0,9145	0,7373	1,60	0,2615	0,5336	0,1395
0,20	0,7561	0,8898	0,6728	1,65	0,2553	0,5268	0,1345
0,25	0,7115	0,8666	0,6166	1,70	0,2493	0,5201	0,1297
0,30	0,6715	0,8449	0,5674	1,75	0,2436	0,5137	0,1251
0,35	0,6355	0,8246	0,5240	1,80	0,2382	0,5074	0,1209
0,40	0,6029	0,8052	0,4855	1,85	0,2330	0,5013	0,1168
0,45	0,5733	0,7870	0,4512	1,90	0,2280	0,4954	0,1130
0,50	0,5463	0,7698	0,4210	1,95	0,2232	0,4896	0.1093
0,55	0,5216	0,7534	0,3930	2,0	0,2186	0,4840	0,1058
0,60	0,4988	0,7379	0,3681	2,5	0,1810	0,4353	0,0788
0,65	0,4779	0,7231	0,3456	3,0	0,1542	0,3967	0,0612
0,70	0,4586	0,7090	0,3251	3,5	0,1342	0,3653	0,0490
0,75	0,4407	0,6956	0,3066	4,0	0,1187	0,3392	0,0403
0,80	0,4240	0,6828	0,2895	4,5	0,1064	0,3170	0,0337
0,85	0,4085	0,6705	0,2739	5,0	0,0964	0,2979	0,0287
0,90	0,3941	0,6587	0,2596	5,5	0,0880	0,2813	0,0248
0,95	0,3805	0,6474	0,2463	6,0	0,0810	0,2666	0,0216
1,00	0,3679	0,6366	0,2342	6,5	0,0750	0,2536	0,0190
1,05	0,3560	0,6262	0,2229	7,0	0,0699	0,2420	0,0169
1,10	0,3448	0,6162	0,2125	7,5	0,0654	0,2315	0,0151
1,15	0,3343	0,6066	0,2028	8,0	0,0614	0,2221	0,0136
1,20	0,3243	0,5973	0,1937	8,5	0,0579	0,2134	0,0124
1,25	0,3150	0,5883	0,1853	9,0	0,0547	0,2055	0,0112
1,30	0,3061	0,5797	0,1774	9,5	0,0519	0,1982	0,0103
1,35	0,2977	0,5714	0,1701	10	0,0494	0,1915	0,0095
1,40	0,2897	0,5633	0,1632	15	0,0331	0,1446	0,0048

Обычно в КМ известна емкость батареи конденсаторов и неизвестны индуктивность и активное сопротивление кон­тура. В этом случае, используя выражения

B = 4tlTt=2t,(izYLCy, А = Ц1а = (t'/I/C0) VLjC (3.15)

находим из табл. 3.1 по AS параметр р и значения А я В. Затем, подставляя найденные Л и В в (3.15), рассчиты­ваем

L=4i2/ (л2В2С) или L—A2U2CoC/i2. (3.17)

Определив значение L, из формулы (3.5) находим ис­комое активное сопротивление контура:

R = 2р]ПТС.

Пример расчета. Определить индуктивность и активное сопротивле­ние контура при заданном импульсе разрядного тока для машины МТК-5001, если известно, что емкость батареи конденсаторов С= = 115 000 мкФ, начальное напряжение иа батарее Ucо=380 В, коэффи­циент трансформации сварочного трансформатора п = 74. Из осцилло­граммы разрядного тока при коротком замыкании контура известно также, что амплитудное значение первичного тока и время до амплиту­ды соответственно равны /ia=793 A; Ги=0,028 с.

По (ЗЛ 6) вычисляем

0,3236.

По табл. 3.1, применяя экстраполяцию, находим Л = 0,4571; р= =0,7037. Рассчитываем индуктивность контура по (3.17), а затем актив - woe сопротивление контура — по (3.18) (оба значения приведены к пер­вичному контуру и обозначаются соответственно L' и R'):

АЮггпС 0.45712-380г-0,115 L' = —jr^~ = 793*

1 13

Приведем параметры ко вторичному контуру, учитывая, что L"=L'/n2 и R"=R'/nK

Тогда

0,0055 , 0,3068

L" = -742------ 1,0-10-» Гн; R" =~^Г

В практике, особенно для вновь изготовленных и нахо­дящихся в длительной эксплуатации КМ с электролити­ческими конденсаторами, необходимо измерять емкость С батареи конденсаторов. Это связано в первую очередь с большими допустимыми отклонениями по емкости конден­саторов (до +50%) при изготовлении и с выходом из строя отдельных конденсаторов и плавких предохраните­лей при эксплуатации. Наиболее простым методом опре­деления емкости С является метод обсчета экспоненты разряда на известное сопротивление. В этом случае раз­ряд описывается формулой

uc = U&e-,h. (3.19)

где ис и b'co — соответственно текущее и начальное напря­жения на конденсаторах; т — постоянная времени, равная ReC, где Re — балластное сопротивление. После несложных преобразований выражение (3.19) приведем к виду, позво­ляющему найти емкость:

Используя экспоненту разряда и зная Ucо, можно лег­ко определить ис для любого удобного значения времени t. Подставив все известные значения в (3.20), можно опре­делить емкость батареи конденсаторов с достаточной для практики точностью. Вычисления еще более упрощаются, если учесть, что в момент t—т имеет место соотношение Wc/^co=0,368. Используя последнее, по экспоненте разря­да легко определить т, а с ней и емкость конденсаторной батареи.