В управлении проектами есть один весьма коварный вопрос. Как можно составить план того, что по большей части существует только в виде идеи'? Выражаясь более научно, возможно или нет планирование в ситуации с большой степенью неопределенности?

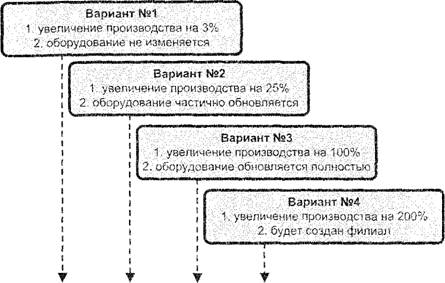
Рассмотрим неопределенность планирования на примере годовых производственных планов завода. На рис. 06 показаны четыре вариан­та производственных плана.

План по варианту №1 составляется очень просто. На предприятии есть фактические данные по всем параметрам производства. Всегда можно найти резервы для небольшого увеличения, скажем, на 3-10% без существенного привлечения новых ресурсов. Поэтому план вари­ант №1 является просто записью уже проверенных на практике резуль­татов. Другое дело вариант №4. Здесь сначала возникает идея, иници­атива создать филиал. В этот момент ничего кроме концетуальной идеи не существует. Может ли персонал завода в этот момент более или менее точно рассчитать бюджет и дать заявку на финансирование, насколько точно можно прогнозировать срок завершения проекта?

Рисунок 06. Варианты годовых производственных планов

Казалось бы, задача не имеет решения: нельзя планировать то, что в принципе неопределенно. На самом деле, методика решения существует.

В руководствах по управлению проектами этот метод называется Work Breakdown Structure (WBS). Для перевода используются значе­ния — Разбиение работ, Декомпозиция работ, Иерархическая структу­ра работ.

К сожалению, практически нигде не описывается, почему этот ме­тод имеет какую-то эффективность. Отсутствие пояснений может заставить относится к WBS как к непонятно зачем - существующему инструменту.

Причина отсутствия пояснений к WBS носит объективный характер. Дело в том, что эффективность метода WBS обусловлена действием знаменитого математического вывода - законом больших чисел. Веро­ятно, авторы учебников и других документов уверены в том, что чита­тели все равно не поймут действие этого закона и потому просто опус­кают его изложение (а может и не знают про такой закон).

Закон больших чисел точно доказан для большого количества си­туаций. Более того, вероятно, закон имеет и некий общечеловеческий смысл, так как его проявление видно в различных сферах жизни. Клас­сический, известный всем пример. В семье с одним ребенком, ребенок может быть или девочкой, или мальчиком. В большом коллективе (на­пример, деревня) количество девочек всегда примерно равняется ко­личеству мальчиков. Чем больше коллектив, тем более высока степень равенства. Отсюда и название закона - закон больших чисел.

Попробуем разобраться в действии этого закона применительно к WBS.

Закон применяется в ситуациях, когда складывают случайные (изна­чально неопределенные) величины. К случайным величинам относит­ся: выпадение орла или решки при бросании монеты, приход трамвая в заданный интервал времени и т. д. Значительная часть случайных ве­личин имеет какое-то среднее значение, а сами величины распределя­ются вокруг этого среднего значения. Например, строительный кирпич керамический полнотельный должен иметь по ГОСТ 530-95 вес 3,5 кг, а размеры 250 х 120 х 65 мм. Реальные кирпичи будут иметь отличаю­щиеся от стандарта, случайные значения. Это отличие будем называть ошибкой.

Фактические показатели проекта являются случайными ве­личинами по отношению к первоначальным, плановым пока­зателям. Отклонение фактических показателей от плановых является ошибкой проекта. В частности, в этой терминоло­гии экономия ресурсов считается ошибкой.

Исходя из сказанного, приведем общую качественную формулиров­ку закона применительно к нашему случаю:

• ошибка суммы случайных (неопределенных) величин меньше, чем ошибка самой величины

Приведем численный пример. Допустим, мы строим дорогу из рель­сов. По чертежам мы должны делать каждый рельс длиной ровно 10 метров. Наше оборудование, на котором нарезаются рельсы, весьма грубое. Поэтому один рельс у нас получается не 10 метров, а 10 метров плюс-минус 1 метр. Другими словами точность (ошибка) длины одно­го рельса составляет примерно 10% от планового значения. Конечно, в реальности трудно представить себе настолько грубое оборудова­ние. Но, для рассматриваемого примера, такая утрированность как раз необходима.

Результаты нашего "производства" приведены в таблице 05. Конеч­но, реального производства рельсов не было. Для длины каждого рель­са использовался генератор случайных чисел программы MS Excel.

На рис. 07 показано, как изменяется ошибка фактической длины до­роги в зависимости от количества рельсов, уложенных в дорогу.

-Я'/- A;' . ^

15 20 25 ЗО ЗЇЇ 40

Рисунок 07. Точность длины дороги в зависимости от количества

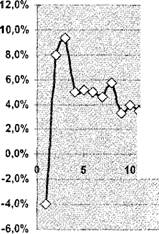
Рельсов

Таблица 06 содержит сводный отчет о строительстве дороги из 36 рельсов.

Итоговые данные демонстрируют удивительный результат. Казалось бы, если каждый рельс имеет отклонение плюс-минус 1 метр, то первое интуитивное ощущение состоит в том, что длина дороги из 36 рельсов будет иметь отклонение плюс-минус 36 метров. Фактически, отклоне­ние составило всего лишь 3,4 метра. Вместо изначальной ошибки 10%, фактическая длина дороги отклоняется от планового значения всего лишь на 0,94%!

Более того, увеличим длину дороги. Пусть теперь дорога состоит из 100 рельсов. Рельсы изготавливаются с той же точностью. Таблицу для случая 100 рельсов, аналогичную таблице 05, не приводим. Оказывает­ся, что теперь фактическая длина дороги будет отклоняться от плано­вого значения всего лишь на 0,32%. То есть, всего лишь 32 сантиметра. Это даже меньше, чем погрешность на одном рельсе — 1 метр. Таким образом, чем больше количество суммируемых случайных элементов, тем выше точность суммы величин.

С какой скоростью растет точность суммы величин? Темп скорости зависит от так называемого в математике распределения вероятностей значений первичной величины. В большинстве случаев действует про­стое правило:

Ошибка суммы случайных величин меньше ошибки самой величины в корень из N, где N - количество суммируемых величин.

Если A =Xj + х, + + xv то:

SA=Sx/ ^N

Как закон больших чисел помогает в управлении проектами? До­пустим, нам нужно подсчитать бюджет (смету) проекта. Разобьем все работы на 100 различных по типу работ, но примерно одинаковых по стоимости. Если стоимость каждой работы на начальном этапе нам из­вестна с точностью 50% относительно будущей фактической величи­ны, то точность всего бюджета составит 5%! Корень из 100 равняется 10, и именно в 10 раз улучшится точность. На начальном этапе точ­ность в 5% более, чем достаточна.

Приведенное правило и составляет основу WBS. Забегая вперед, следует сказать, что WBS, декомпозиция работ нужна не только для повышения точности расчетов.

Совершенно аналогичные рассуждения можно привести и для по­вышения точности расчета длительности проекта. Нужно разбить все работы на примерно равные по длительности, оценить длительность каждой отдельной работы и получить общую длительность.

При применении закона больших чисел нужно учитывать следую­щие замечания.

Замечание первое.

Закон эффективно работает, если производится разбиение на при­мерно равнообъемные работы. В противном случае закон работать не

Будет. Например, проект заключается в покупке офисного здания и вы­полнения в нем косметического ремонта. Стоимость покупки 1 милли­он долларов, стоимость ремонта 50 тысяч. Суммарный бюджет 1050 тысяч, при этом как точно ни считать стоимость ремонта, точность бюджета будет определяться точностью цены покупки здания. Понят­но, что цену покупки нельзя подвергнуть декомпозиции. Поэтом}' для подобных проектов надо сразу смириться с тем, что бюджет и сроки проекта будут на начальном этапе известны с небольшой точностью.

Замечание второе. Насколько подробно нужно производить декомпозицию?

Может возникнуть вопрос: а если мы сделаем разбиение не на 100 элементов, а на 10 тысяч, насколько здесь увеличится точность? Ока­зывается, что математическая статистика здесь ставит заслон - достичь абсолютной точности не удастся. Не вдаваясь в дебри математики, можно привести эмпирическое правило: достаточно разбиения на 100- 300 величин. Это количество дает вполне приемлемое увеличение точ­ности с экономической точки зрения. Затраты на более точные расчеты могут превысить разумные величины.

Замечание третье.

При выполнении декомпозиции нужно учесть все возможные ра­боты. Если в перечень работ включены 95% работ, а про 5% просто забыли, то, как бы точно ни считать учтенные 95% работ, суммарный плановый бюджет все равно окажется меньше фактического на 5%і Еще более важно учесть все работы при расчете длительности проек­та. Некоторые работы могут иметь критическое значение. Например, в строительных проектах получение разрешения на ведение строитель­ных работ. Прямые затраты на получение разрешения минимальны, но если разрешения нет, то весь проект может остановиться.

Последнее замечание прямо связано с принципом комплексности в управлении проектами:

Не столь важно, как точно и детально мы управляем отде­льными элементами проекта, важно, чтобы мы управляли всеми элементами проекта!