При использовании поверхностных и нормальных волн для контроля деталей сложной формы в ряде слу­чаев важно знать, как распространяются УЗК на кривых поверхностях и в оболочках. Однако эти вопросы в ульт­развуковой дефектоскопии не рассматриваются[10].

Распространение упругих волн на кривой поверхности (или в кривой оболочке) может быть объяснено с позиций геометрической акустики [14], дифференциальной гео­метрик [16, 17] и теории поверхностей [18], без сложных математических выкладок.

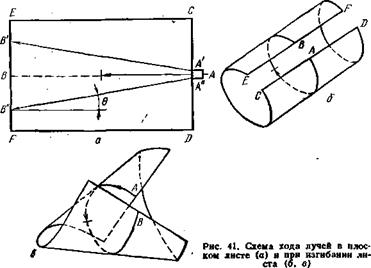
Рассмотрим пучок лучей УЗК, распространяющихся в тонком плоском листе от одного края к другому (рис. 41). В данном случае звуковое поле ограничено толщи­ной листа, а в плоскости листа волны распространяются

расходящимся пучком лучей. При достаточно малой толщине листа (при 6-*-0) можно считать, что каждая элементарная волна распространяется в плоскости листа по траектории, представляющей собой прямую линию (луч). При этом центральный луч АВ падает на проти­воположную кромку листа под углом 90°, а боковые лу­чи А'В' и А"В" за счет расхождения пучка — под углами 90—0°.

Из теории поверхностей известно, что прямая, лежа­щая на любой поверхности, представляет собой геодези­ческую линию, являющуюся кратчайшей и прямейшей на поверхности. Следовательно, лучи (прямые линии) АВ, А'В' и А"В" являются геодезическими линиями на плоской поверхности.

Если изгибать лист в направлении, перпендикуляр­ном распространению центрального луча АВ, придавая ему, например, цилиндрическую форму, то линии АВ,

т

А'В' и А"В" из прямых превратятся в кривые. Однако они также остаются геодезическими.

Одно из определений геодезических линий как «пря­мейших» связано с положением поверхности в простран­стве, а именно: дуга геодезической линии во всех точках имеет наименьшую кривизну по сравнению со всеми теми кривыми на поверхности, которые имеют с дугой геоде­зической линии общую касательную в данной точке. Это свойство определяет геодезическую линию на всем ее протяжении, если задать одну из ее точек и ее направ­ление в этой точке. Такую линию можно получить, если в заданной точке и в заданном направлении протянуть упругую прямую спицу и пригибать ее к поверхности так, чтобы она могла двигаться по поверхности только вдоль самой себя. Так как спица сопротивляется всяко­му искривлению, то она примет вид геодезической линии [17].

Аналогичная картина наблюдается при изгибании плоского листа. Любой ультразвуковой луч, подобно упругой спице, сопротивляется искривлению (как если бы мы его «пригибали» к кривой поверхности) и распро­страняется по траектории, являющейся прямейшей и кратчайшей на поверхности. Такой траекторией может быть только геодезическая.

Высказанные соображения можно подтвердить экс­периментально. Возьмем металлический лист, изготов­ленный, например, из алюминиевого сплава АМГ тол­щиной 1 мм с взаимно параллельными сторонами разме­рами 1000X600 мм. В средней части листа параллельно сторонам CD и EF сделаем поперечный надрез глубиной около 0,2 мм, длиной 20 мм (рис. 41, а).

На одной из сторон CD или EF листа установим в приспособлении прямой преобразователь, излучающий в торец продольные волны. Приспособление должно обес­печивать устойчивое положение преобразователя на тор­це листа и постоянный акустический контакт. При этом УЗК распространяются вдоль листа до противоположно­го конца и отражаются обратно.

Перемещая преобразователь вдоль кромки, опреде­лим такое его положение, при котором на экране дефек­тоскопа возникает наиболее интенсивный сигнал от над­реза. Зафиксируем положение центра излучения преоб­разователя по отношению к надрезу. Опыты покажут, что максимальное отражение УЗК от надреза происходит тогда, когда центр излучения преобразователя находит-

ся против середины надреза, т. е. на прямой линии АВ (см. рис. 41, а), являющейся кратчайшим расстоянием от преобразователя до надреза.

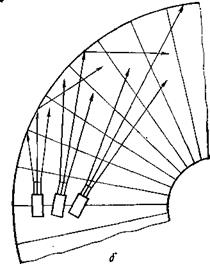
Затем будем изгибать лист в цилиндрические и кони­ческие поверхности с различной кривизной (рис. 41, б, в). Многократные опыты покажут, что и в этом случае мак­симальная амплитуда сигналов будет при том же поло­жении преобразователя, что и до изгибания листа, т. е. центральный луч распространяется в плоском и изогну­том листах по кратчайшему пути АВ, длина которого при изгибе листа не изменяется. Следовательно, цент­ральный луч УЗК распространяется на плоских и кривых поверхностях по геодезическим траекториям. Очевидно, что этот вывод справедлив и для других лучей пучка, например лучей А'В' и А"В".

На основании изложенного можно сформулировать следующий более общий закон распространения УЗК: ультразвуковые волны распространяются и отражаются в любой изотропной упругой среде и на любой ее глад­кой плоской или кривой поверхности по геодезическим траекториям.

Такой вывод представляет большой практический ин­терес и открывает новые возможности в совершенствова­нии методики ультразвукового контроля деталей слож­ной формы.

Рассмотрим распространение поверхностных и нор­мальных волн на цилиндрической, конической и шаро­вой поверхностях.

Для цилиндрической поверхности геодезическими ли­ниями, как известно, являются меридианы, окружности и винтовые линии. Проанализируем несколько случаев:

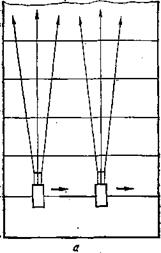
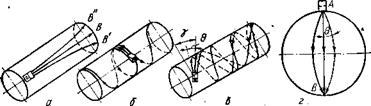
1. Пучок лучей направлен вдоль образующей цилинд­ра (рис. 42, а). Так как преобразователь посылает вдоль

цилиндрической поверхности расходящийся пучок лучей, то только центральный и близлежащие к нему лучи на­правлены вдоль меридиана (образующей); остальные лучи пересекают образующие под небольшими углами, изменяющимися от 0 до 0 (где 0 — половина угла рас­хождения пучка лучей при излучении преобразователя в плоскую поверхность), т. е. распространяются по винто­вым линиям с большим шагом.

2. Пучок лучей направлен по окружности (рис. 42, б). В этом случае только центральный луч распространяет­ся по окружности. Остальные лучи пересекают образую­щие под углами от 90° до 90—0 и распространяются па винтовым линиям с небольшим шагом вправо и влево от преобразователя.

При таком облучении иногда могут быть получены отражения центрального луча от противоположной сто­роны преобразователя: на экране дефектоскопа появится «концевой» сигнал. При прозвучивании цилиндрической поверхности большого диаметра «концевого» сигнала мо­жет и не быть.

3. Пучок лучей направлен под углом к образующей цилиндра (рис. 42, в). В этом случае лучи распростра­няются по винтовым линиям: причем если угол поворота преобразователя у (у — угол между центральным лучом и касательной к окружности) больше или равен 0, то волны обтекают цилиндр и распространяются в направ­лении поворота преобразователя. Если угол у<0, та часть лучей (в данном случае левых) распространяется в направлении, противоположном повороту преобразова­теля. Из изложенного следует, что при любом облучении цилиндрической поверхности на экране ЭЛТ могут воз­никнуть сигналы, соответствующие отражению части волн от дефектов, расположенных «в стороне» от направ­ления прозвучивания и ориентированных на поверхности более благоприятно к боковым лучам, чем к централь­ному.

Для конической поверхности геодезическими ЛИНИЯМИ - являются меридианы и винтовые ЛИНИИ.

Если установить преобразователь, например, на по­верхность усеченной конической трубы так, чтобы пучок был направлен вдоль образующей (со стороны большега или меньшего основания), то он будет распространяться так же, как показано на рис. 42, а.

Если преобразователь установить так, чтобы пучок лучей был направлен «по окружности», то здесь будет

наблюдаться иная картина, чем при аналогичном про - звучивании цилиндрической поверхности. При установке преобразователя на цилиндрической трубе перпендику­лярно образующей центральный луч пучка УЗ К пересе­кает их под прямым углом. При аналогичном расположе­нии преобразователя на конической поверхности центральный луч перпендикулярен образующей только в месте установки преобразователя. На других участках

Рас. 43. Схема хода лучей нормальных воли иа развертке цилиндрической
(о) и усеченной конической (б) труб

центральный луч, распространяясь, пересекает образую­щие под другими углами, уменьшающимися с расстояни­ем от преобразователя. Это хорошо видно на развертках цилиндрической и конической труб (рис. 43).

Известно, что в цилиндрических и конических труб­чатых изделиях дефекты ориентированы, как правило, вдоль образующих. Для надежного их выявления ульт­развуковой пучок (вернее центральный луч пучка УЗК) направляют на дефект под углом, равным или близким к 90°. В этом случае большая часть энергии УЗК отра­зится от дефекта в направлении преобразователя. Поэто­му при контроле круглой трубы преобразователь уста­навливают так, как показано на рис. 43, а, и перемеща­ют его вдоль образующей. а

При контроле конической трубы для выявления де­фектов, ориентированных вдоль образующих, необходимо преобразователь перемещать и поворачивать в сторону меньшего основания (рис. 43, б).

Для шаровой поверхности геодезическими линиями являются большие круги. При возбуждении в точке А поверхности шара нормальных или поверхностных волн они распространяются в направлении прозвучивания расходящимся пучком с углом расхождения, равным 2 0 (рис. 42,г). Здесь максимальное расхождение пучка на­блюдается на экваторе шаровой поверхности (если точ­ку Л установки преобразователя принять за полюс). За экватором пучок сужается до точки В противоположного полюса. При дальнейшем распространении волн картина повторяется.

Такое представление о распространении волн на кри­вых поверхностях (и в оболочках) можно перенести на поверхности, имеющие более сложную форму. Задача заключается в том, чтобы определить геодезические ли­нии на данной поверхности. Можно отметить, что наибо­лее просто определяются траектории на поверхностях, тел вращения. У них меридианы — всегда геодезические линии.

Вообще іке отыскание геодезических линий поверхно­сти сводится к интегрированию системы обыкновенных дифференциальных уравнений второго порядка [18].