За расчетную нагрузку принимают максимальную величину удель­ной нагрузки, распределенной по линии контакта зубьев:

Q=FJK/K, (8.4)

Где F„ — нормальная сила в зацеплении; K=KaKpKv — коэффициент расчетной нагрузки; Ка — коэффициент распределения нагрузки между зубьями; Кр — коэффициент концентрации нагрузки; К» — коэффициент динамической нагрузки; h — суммарная длина линии контакта зубьев.

Концентрация нагрузки и динамические нагрузки различно вли­яют на прочность по контактным и изгибным напряжениям. Со­ответственно различают Кн=KHaKmKHv — в расчетах по контакт­ным напряжениям и KF=KFaKFpKFv — в расчетах по напряжениям изгиба.

Коэффициент распределения нагрузки между зубьями Ка опреде­ляется в зависимости от степени точности (п^) изготовления зуб­чатых колес по нормам плавности. Он учитывает влияние ошибок окружного шага и направления зубьев на величину /z в ненагружен - ной передаче. Для прямозубых передач:

Кна = 1 + 0,06 (ист— 5)< 1,25; для косозубых передач:

*Яа=1 + С(лст-5К1,6,

Где С=0,15, если твердости поверхностей зубьев шестерни и колеса Hi и #2 >350 НВ и С=0,25 при Нг и 350 НВ или ^>350 НВ, а #2^350 НВ; 5<wCT<9. В расчетах на прочность по напряжениям изгиба полагают KFa=KHa. Отметим, что для точноизготовленных передач (лст=5) КНа= 1.

Коэффициент концентрации нагрузки Концентрация или не­равномерность распределения нагрузки по длине зуба связана с деформацией валов, корпусов, опор и самих зубчатых колес, а также с погрешностями изготовления и сборки передачи. Поясним это сложное явление на примере, учитывающем только прогиб валов.

На рис. 8.13 изображено взаимное расположение зубчатых ко­лес при деформированных валах в случаях: симметричного (рис. 8.13, а), несимметричного (рис. 8.13, б) и консольного (рис. 8.13, в) расположения колес относительно опор. Валы прогиба­ются в противоположные стороны под действием сил в зацепле­нии (рис. 8.13, г).

Рис. 8.13

При симметричном расположении опор прогиб валов не вы­зывает перекоса зубчатых колес и, следовательно, почти не нару­шает распределения нагрузки по длине зуба. Это самый благопри­ятный случай. При несимметричном и консольном расположении опор колеса перекашиваются на угол у, что приводит к наруше­нию правильного касания зубьев. Если бы зубья были абсолютно жесткими, то они соприкасались бы только своими концами (см. рис. 8.13, д, на котором изображено сечение зубьев плоскостью зацепления). Деформация зубьев уменьшает влияние перекосов и в большинстве случаев сохраняет их соприкасание по всей длине (рис 8.13, е). Однако при этом нагрузка перераспределяется в соот­ветствии с деформацией отдельных участков зубьев (рис. 8.13, ж). Отношение

Где — средняя интенсивность нагрузки.

При прочих равных условиях влияние перекоса зубьев увеличива­ется с увеличением ширины колес BW9 поэтому ее ограничивают (см. ниже).

Концентрация нагрузки увеличивает контактные напряжения и напряжения изгиба. Для уменьшения опасности выламывания углов зубьев на практике применяют колеса со срезанными углами (см. рис. 8.13, з). Если колеса изготовлены из прирабатывающихся материалов (например, стали с твердостью Н < 350 НВ), то концен­трация нагрузки постепенно уменьшается вследствие повышенного

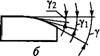
Местного износа. При постоянной нагрузке передачи приработка зубьев может полностью устранить концентрацию нагрузки. Пере­менная нагрузка (рис. 8.14, а) сопровождается ступенчатой прира­боткой зубьев (см. продольное сечение зуба, изображенное на рис. 8.14, б). При ступенчатой приработке концентрация нагрузки снижа­ется лишь частично. Ступенчатая приработка, или огранка зубьев, связана с изменением деформации валов и угла перекоса в зависи­мости от величины нагрузки. Каждому углу перекоса соответствует своя площадка соприкасания зубьев, образовавшаяся от приработ­ки при данной нагрузке. Благоприятное влияние приработки зубьев на уменьшение концентрации нагрузки проявляется в значительно меньшей степени при высокой твердости поверхности зубьев (>350 НВ), а также в передачах с высокими окружными скоростями 15 м/с). При больших скоростях между зубьями образуется масляный слой, защищающий их от износа. Для уменьшения концентрации нагрузки при высокой твердости зубьев и высоких окружных скоро­стях рекомендуют применять относительно неширокие колеса или придавать зубьям бочкообразную форму (рис. 8.14, в) путем измене­ния глубины врезания по длине зуба.

При конструировании передачи необходимо учитывать все фак­торы, влияющие на концентрацию нагрузки, и в первую очередь не применять нежестких валов, опор и корпусов.

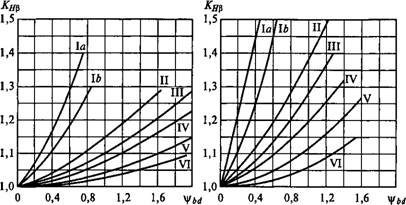
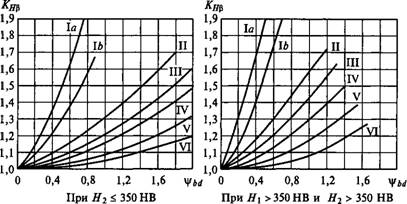
Расчет коэффициента Кр связан с определением угла перекоса у. При этом следует учитывать не только деформацию валов, опор и самих колес, но также приработку зубьев, ошибки изготовления и сборки. Все это затрудняет точное решение задачи. Для прибли­женной оценки Кр рекомендуют графики, составленные на основе расчетов и практики эксплуатации (рис. 8.15). Графики рекоменду­ют для передач, жесткость и точность изготовления которых удов­летворяет нормам, принятым в редукторостроении. Кривые на графиках соответствуют различным случаям расположения колес относительно опор, изображенных на схемах рис. 8.15 (кривые I а — шариковые опоры, Lb — роликовые опоры). Влияние ширины колеса на графиках учитывают коэффициентом Влияние

Приработки зубьев учиты­вают тем, что для различ­ной твердости материа­лов даны различные гра­фики. Графики разработа­ны для распространенно­го на практике режима ра­боты с переменной на­грузкой и окружной ско­ростью v<15 м/с. Рис. 8.14

При постоянной нагрузке, при твердости поверхности зуба коле­са #2 <350 НВ и V< 15 м/с можно принимать Кр= 1.

Коэффициент динамической нагрузки К^. Коэффициентом К, учи­тывают только так называемые внутренние динамические нагрузки, присущие самой зубчатой передаче. Внешние динамические нагруз­ки, связанные с режимом работы двигателя и исполнительного
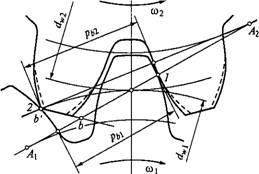
механизма, будут учтены при выборе допускаемых напряжений для переменных режимов нагружения (см. § 8.13). Выше было указано, что погрешности нарезания зубьев являются причиной непостоянст­ва мгновенного передаточного отношения. Это значит, что при (х)х = const, const и dto2/d/^0. В зацеплении появляется допол­нительный динамический момент Tv=Jdco2/Dt, где J — момент инер­ции ведомых масс. Основное влияние на величину динамических нагрузок имеют ошибки основного шага рь. На рис. 8.16 изображен случай зацепления, при котором шаг колеса больше шага шестерни, т. е. ры>Ръ-

По закону эвольвентного зацепления, I=Dw2Jdw,= const при по­стоянном положении полюса зацепления или при положении всех точек зацепления на линии зацепления АХА2. Если ры>рьи то вто­рая пара зубьев вступает в зацепление в точке Ъ' до выхода на ли­нию зацепления в точку Ъ. При этом изменяется мгновенное передаточное отношение. В точке Ъ' происходит так называемый кромочный удар[19], который не только увеличивает динамическую нагрузку, но также способствует задиру поверхности зубьев. Для уменьшения эффекта кромочного удара применяют фланкирован­ные зубья, у которых верхний участок эвольвенты выполняют с отклонением в тело зуба (на рис. 8.16 показан штриховой линией[20]).

Величина дополнительных динамических нагрузок зависит от ошибки шага, окружной скорости, присоединенных масс, упругости системы и пр.

Коэффициент К, опре­деляют по формуле

£ = 1 + Qjq,

Где Qv — удельная дина­мическая нагрузка; Q — Удельная расчетная рабо­чая нагрузка в зоне ее на­ибольшей концентрации.

Расчет А* не менее ело- Рис. 8.16

Жен, чем расчет Для
приближенной оценки рекомендуют табл. 8.3*. Величина К^ неско­лько меньше при высокой твердости материала (группа б). Это объясняется не уменьшением Qv, а увеличением Q вследствие увели­чения допускаемых контактных напряжений (см. § 8.13).

Примечания: 1. Твердость поверхностей зубьев

_Г#,< 350 НВ, <350 НВ;

Q нх>45 HRC, Я2<350 НВ;

Ь-н^45 HRC, Н2>45 HRC.

2. Верхние числа — прямозубые, нижние — косозубые колеса.