Расчет на прочность прямозубых и косозубых цилиндрических передач стандартизован ГОСТ 21354—87. В курсе «Детали машин» изучают основы такого расчета. При этом вводят некоторые упро­щения, мало влияющие на результаты расчетов для большинства случаев практики.

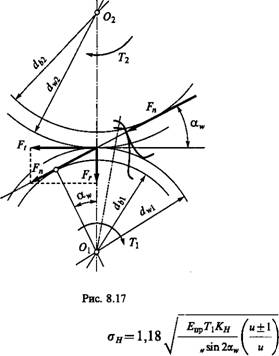
Силы в зацеплении. На рис. 8.17 Fn — нормальная сила, направ­ленная по линии зацепления как общей нормали к рабочим поверх­ностям зубьев. Силы, действующие в зацеплении, принято прик­ладывать в полюсе зацепления. При этом силу Fn переносят в по­люс и раскладывают на окружную Ft и радиальную Fr. Такое раз­ложение удобно при расчете валов и опор. По заданным TndОпре­деляют

(8.5)

И через нее выражают все другие составляющие:

Fr=Ft tgaw, Fn=FJCosaw. (8.6)

Расчет прочности зубьев по контактным напряжениям. Исследова­ниями установлено, что наименьшей контактной усталостью об­ладает околополюсная зона рабочей поверхности зубьев, где на­блюдается однопарное зацепление (см. рис. 8.5). Поэтому расчет контактных напряжений принято выполнять при контакте в полюсе зацепления (рис. 8.18). Контакт зубьев можно рассматривать как контакт двух цилиндров с радиусами рг и р2- При этом контактные напряжения определяют по формуле (8.2), а именно:

Ая=0,4187?Дф/Рпр - (8.7)

Для прямозубых передач с учетом формул (8.4)...(8.6)

Q=FJChIK=FtKH/(bw cos a,)=2TlKH/(dwlbw cosa*). (8.8) Радиусы кривизны эвольвент зубьев в точке контакта (рис. 8.18)

Р = Wvi sinaw)/2; p2 = (dw2 sinaw)/2. По формуле (8.3), 2 2

1 _ 1 + 1 _

=Y~.—(—). (в.») Dw Smaw и J

«1*

Pup Pi Pi dwl sinaw sinaw 2

D^i sina^

Где U = Dw2/Dwl=Z2/Zu знак « + »— для наружного, а « — » — для вну­треннего зацепления. Подставляя в формулу (8.7) и заменяя cosawsinaw=(sin2aw)/2, получаем

(8.10)

Параметр и=г2/гг по ГОСТ 16532—70 называют передаточным числом и определяют как отношение большего числа зубьев к мень­шему независимо от того, как передается движение: от Zx к Z2 или от Z2 к Z. Это передаточное число и отличается от передаточного отношения /, которое равно отношению угловых скоростей ведуще­го колеса к ведомому и которое может быть меньше или больше единицы, положительным или отрицательным. Применение и вме­сто I связано только с принятой формой расчетных зависимостей для контактных напряжений [см. вывод формулы (8.9), где Рщ> выра­жено через D (меньшее колесо), а не через D2 (большее колесо)]. Величина контактных напряжений, так же как и передаточное число и, не зависит от того, какое колесо ведущее, а величина передаточ­ного отношения I зависит. Однозначное определение и позволяет уменьшить вероятность ошибки при расчете. Передаточное число И относится только к одной паре зубчатых колес. Его не следует применять для обозначения передаточного отношения многосту­пенчатых редукторов, планетарных, цепных, ременных и других передач. Там справедливо только обозначение /.

Величины расчетных контактных напряжений одинаковы для шестерни и колеса. Поэтому расчет выполняют для того из колес

Ox T{ Рис. 8.18

Пары, у которого меньше допускаемое напряжение [<тя] — см. ниже (чаще это бывает колесо, а не шестерня).

Формулу (8.10) используют для проверочного расчета, когда все необходимые размеры и другие параметры передачи известны. При проектном расчете необходимо определить размеры передачи по заданным основным характеристикам: вращающему моменту Тг или Т2 и передаточному числу и.

С этой целью формулу (8.10) решают относительно D или А. Другие неизвестные параметры оценивают приближенно или выбирают по рекомендациям на основе накопленного опыта. В нашем случае принимаем aw«a=20° (sin2a«0,6428), KHv&

«1,15 (этот коэффициент зависит от окружной скорости V, кото­рая пока неизвестна, поэтому здесь принята некоторая средняя величина — см. табл. 8.3). При этом из составляющих коэффициен­та Кн [см. формулу (8.4)] остаются КНа и Кщ. Далее обозначаем — коэффициент ширины шестерни относительно диа­метра.

Подставляя в формулу (8.10) и решая относительно du находим

(8.11)

Решая относительно межосевого расстояния Aw, заменяем «Т2/и; Dl=2Aw/(U±L) и вводим L/ba=Bw/Aw — коэффициент ширины колеса относительно межосевого расстояния. После преобразований с учетом зависимости

Фм=0,5фьа(и±1) (8.12)

Получим

3 iещ>т2кнакнр

Я„=0,85(и±1) I 7 2 7 (8.13)

При расчетах передач с цилиндрическими зубчатыми колесами чаще используют формулу (8.13), так как габариты передачи опре­деляет преимущественно межосевое расстояние. По тем же сооб­ражениям в формуле (8.13) момент Т заменяют на Т2. Величина момента Т2 на ведомом валу является одной из основных харак­теристик передачи, интересующих потребителя (обычно указывает­ся в техническом задании).

, J Т(«±л / V [°н]2и2фьа,

В приложении к ГОСТ 21354—87 для стальных зубчатых колес формулы (8.11) и (8.13) записаны в виде

________ (8.14)

/ ТоКш I

Aw=Ka(u±)

Где кд и ка — вспомогательные коэффициенты, полученные в результате выноса числового значения Е^ из-под знака радикала при КНа = 1, в формулах раз­ные единицы одинаковых физических величин: Т— в Нм, D и Aw — в мм, а л — в МПа.

Для стальных прямозубых колес #</=780 (МПа)1/3, Ка=490 (МПа)1/3, для косо - зубых А^=680 (МПа)1/3, Ка=430 (МПа)1/3.

Вследствие этих операций не соблюдаются правила независимости расчетных формул от системы единиц физических величин. Поэтому формулы (8.14) нецелесо­образно применять в учебном процессе.

Расчет допускаемого напряжения [<тя] см. в § 8.13. Величи­ну Кщ оценивают по рис. 8.15 в соответствии с заданной (или выбранной) схемой передачи и величиной j/bd, которую опреде­ляют по формуле (8.12), где фьа заранее выбирают по рекомендаци­ям табл. 8.4. При выборе учитывают следующее. Увеличение фЬа или относительной ширины колес позволяет уменьшить габари­ты и массу передачи, но вместе с этим требует повышенной жест­
кости и точности конструкции. В противном случае возрастает неравномерность распределения нагрузки по ширине зубчатого вен­ца. Может оказаться, что положительное влияние увеличения шири­ны колес не компенсирует вредного влияния увеличения неравно­мерности нагрузки. Влияние различных факторов на неравномер­ность нагрузки рассмотрено в § 8.5.

Таблица 8.4 Редукторы при расположе­нии колес относительно опор (см. рис. 8.13) Коэффициент ширины колеса Твердость рабочих поверхностей зубьев #2 <350 НВ или Я, и #2 < 350 НВ Я, и #2 >350 НВ Симметричное ФЬа 0,315...0,5 0,25...0,315 Ф^т&х 1,2...1,6 0,9...1,0 Несимметричное ФЬа 0,25...0,4 0,2...0,25 Ах 1,0...1,25 0,65...0,8 Консольное ФЬа 0,2...0,25 0,15...0,2 0,6...0,7 0,45...0,55

Примечания: 1. Для шевронных колес при Bw, равной сумме полушевронов, увеличива­ют в 1,3...1,4 раза. 2. Для подвижных колес коробок скоростей 3. Большие величины — для постоянных и близких к ним нагрузок. 4. Для многоступенчатых редукторов, в которых нагрузка увеличивается от ступени к ступени, в каждой последующей ступени величины фьа, фьск принимают больше на 20...30%, чем в предыдущей. Это способствует хорошему соотношению размеров колес (см. § 8.9). Если при расчете выбирают фьа, то расчетную величину Bw проверяют по условию

Межосевое расстояние Aw для нестандартных редукторов округ­ляют по ряду: Яа40: ...80; 85; 90; 95; 100; 105; 110; 120; 125; 130, далее через 10 до 260 и через 20 до 420...

Для стандартных редукторов общего назначения, изготовляе­мых специализированными заводами, большое значение имеет ограничение числа типоразмеров корпусных деталей, когда в одном корпусе можно изготовить несколько редукторов с различными характеристиками. С этой целью по ГОСТ 2185—66 установлены основные параметры таких редукторов:

Стандартные межосевые расстояния aw:

1- Й ряд — 40, 50, 63, 80, 100, 125, 160, 200, 250, 315, 400, ...

2- Й ряд — 140, 180, 225, 280, 355, 450, ...

Стандартные числовые значения фъа - 0,1; 0,125; 0,16; 0,2; 0,25; 0,315; 0,4; 0,5; 0,63; 0,8; 1,0; 1,25.

Стандартные номинальные передаточные числа и:

1- Й ряд — 1,0; 1,25; 1,6; 2,0; 2,5; 3,15; 4,0; 5,0; 6,3; 8,0

2- Й ряд — 1,12; 1,4; 1,8; 2,24; 2,8; 3,55; 4,5; 5,6; 7,1; 9,0; 11,2

Допускаемое отклонение ±4%.

Выбор модуля и числа зубьев. В формуле (8.10) модуль и число зубьев непосредственно не участвуют. Они входят в эту формулу
косвенно через Du который определяется произведением Mzx. Из этого следует, что величина контактных напряжений ан не зависит от модуля или числа зубьев в отдельности, а определяется только их произведением или диаметрами колес. По условиям контактной прочности при данном dx модуль передачи может быть сколь угод­но малым, лишь бы соблюдалось равенство Mzx — D.

Минимально допускаемую величину модуля можно определить из условия прочности зубьев на изгиб по формуле (8.20). Однако при таком расчете в большинстве случаев получают зацепления с очень мелкими зубьями, применение которых практически ограни­чено. Поэтому величину т обычно выбирают, ориентируясь на рекомендации, выработанные практикой, и затем проверяют изгиб - ную прочность зубьев. В этих рекомендациях учитывают следу­ющее.

Мелкомодульные колеса с большим числом зубьев предпочтитель­ны по условиям плавности хода передачи (увеличивается ва, см. § 8.2) И экономичности. При малых т уменьшаются потери на трение (уменьшается скольжение), сокращается расход материала (умень­шается наружный диаметр Da=D+2H*M) и экономится станочное время нарезания зубьев (уменьшается объем срезаемого мате­риала).

Крупномодульные колеса с большим объемом зубьев дольше про­тивостоят износу, могут работать длительное время после начала выкрашивания, менее чувствительны к перегрузкам и неоднород­ности материала (дефекты литья и т. п.). При мелком модуле возрастают требования к точности и жесткости передачи, так как увеличивается возможность поломки зубьев вследствие концент­рации нагрузки, в особенности при перегрузках. При ориентировоч­ной оценке величины т можно использовать рекомендации табл.

8.5.

Таблица 8.5

Фт—bw/m, Не более

Конструкция

45...30 30...20 30...20 20... 15 15...10

Высоконагруженные точные передачи, валы, опоры и корпуса повы­шенной жесткости:

Ж 350 НВ

#>350 НВ

Обычные передачи редукторного типа в отдельном корпусе с до­статочно жесткими валами и опорами (и другие аналогичные):

Ж 350 НВ

#>350 НВ

Грубые передачи, например с опорами на стальных конструкциях (крановые и т. п.) или с плохо обработанными колесами (литые), а также открытые передачи, передачи с консольными валами (коничес­кие), подвижные колеса коробок скоростей

Примечание. Меньшие фт — для повторно-кратковременных режимов работы, значи­тельных перегрузок и средних скоростей; бблыние фт — для длительных режимов работы, небольших перегрузок и высоких скоростей; Н — твердость поверхности зубьев колеса.

Выбрав по этой таблице фт, определяют

(8.15)

Т = Ь„1фт,

Где

(8.16)

1W.

К=фы4 = фъа. а,

Модуль т согласуют со стандартом (см. табл. 8.1). Для силовых передач обычно рекомендуют принимать т^ 1,0 мм.

При известном модуле определяют и уточняют все остальные параметры передачи.

(8.17)

Для передач без смещения и при xz=0

Di=2a/(u±l); z—dxm z2=zxu d2 — mz2 a = 0,5(rf2±^i).

Должно быть Zx >Z^N, где Z^ — по табл. 8.6.

Для уменьшения шума в быстроходных передачах рекомендуют брать z^ 25. Для окончательного утверждения выбранной вели­чины модуля необходимо проверить прочность по напряжениям изгиба по формуле (8.19).

В случае неудовлетворительного результата изменяют т и уточ­няют Zx и Z2.

При проверке можно получить aF значительно меньше [о>], что не является противоречивым или недопустимым, так как нагру­зочная способность большинства передач ограничивается контакт­ной прочностью, а не прочностью на изгиб. Если напряжение aF превышает допускаемое, то применяют колеса, нарезанные с положительным смещением инструмента, или увеличивают т. Это значит, что в данной передаче (при данных материалах) решающее значение имеет не контактная прочность, а прочность на изгиб. На практике такие случаи встречаются у колес с высоко­твердыми зубьями при Н>50...60 HRC (например, цементирован­ные зубья).

Расчет прочности зубьев по напряжениям изгиба. Зуб имеет слож­ное напряженное состояние (см. рис. 8.10). Наибольшие напряжения изгиба образуются у корня зуба в зоне перехода эвольвенты в гал­тель. Здесь же наблюдается концентрация напряжений. Для того чтобы по возможности просто получить основные расчетные зави­симости с учетом влияния основных параметров на прочность зубьев, рассмотрим вначале приближенный расчет, а затем введем
поправки в виде соответствующих коэффици­ентов. Допустим следующее (рис. 8.19):

1. Нагрузка в зацеплении передается одной парой зубьев и приложена к вершине зуба. Практика подтверждает, что этот худший слу-

<aw чай справедлив для 7-й, 8-й и более низких степеней точности, ошибки изготовления кото­рых не могут гарантировать наличие двухпар - ного зацепления. Например (см. рис. 8.16), ошибки шага приводят к тому, что зубья начи­нают зацепляться вершинами еще до выхода на линию зацепления. При этом вместо те­оретического двухпарного зацепления будет однопарное.

2. Зуб рассматриваем как консольную бал­ку, для которой справедливы гипотеза плоских сечений или методы расчетов, известные из курда «Сопротивление материалов». Фактичес­ки зуб подобен выступу, у которого размеры поперечного сечения соизмеримы с его высо­той. Точный расчет напряжений в таких элеме­нтах выполняют методами теории упругости [35]. Результаты этого расчета используют для уточнения приближенного расчета путем вве­дения теоретического коэффициента концент­рации напряжений (см. ниже).

Силу Fn переносим по линии действия на ось симметрии зуба и раскладываем на составляющие Ft и Fr. При этом радиус приложе­ния окружной силы Ft будет несколько больше радиуса начальной окружности. Пренебрегая этой разностью, для расчета сил Ft и Fr сохраняем формулы (8.5) и (8.6). Напряжение в опасном сечении, расположенном вблизи хорды основной окружности,

<Тиз - ^=Ftli W- Fr/A,

Где W^B^Je — момент сопротивления сечения при изгибе; А — =ЬН^ — площадь; Bw, S и I указаны на рис. 8.19.

Знак «—» в формуле указывает, что за расчетные напряже­ния принимают напряжения на растянутой стороне зуба, так как в большинстве случаев практики именно здесь возникают тре­щины усталостного разрушения (для стали растяжение опаснее сжатия).

T

Размеры / и S неудобны для расчетов. Используя геометрическое подобие зубьев различного модуля, их выражают через безразмер­ные коэффициенты:

R = Ljm и S,=S/M,

Где m — модуль зубьев.

После подстановки и введения расчетных коэффициентов полу­чают

FfoV w tg^l

0>=---- ---- :------- Ат,

B^ltf)2 / J

Где KF — коэффициент расчетной нагрузки (см. § 8.5); Кт — теоре­тический коэффициент концентрации напряжений. Далее обозначают

— коэффициент формы зуба (для наружных зубьев; рис. 8.20).

Для колес с внутренними зубьями приближенно можно прини­мать 7^=3,5...4, большие величины — при меньших z.

При этом для прямозубых передач расчетную формулу записы­вают в виде

<7,= YfsFtKp/ (ЬцЛг) < [Ы (8.19)

Где [aF] —допускаемое напряжение изгиба (см. § 8.13).

Для проектных расчетов по напряжениям изгиба формулу (8.19) решают относительно модуля путем замены Bw = ф„т, Ft=2Txldu Dx = Zxm, тогда

И далее, принимая приближенно KFv—1,5 (см. табл. 8.3), получают

Ж = УЪТхКРаКгр YFsKzx фт [aF]). (8.20)

Величины Zx и J/M задают согласно рекомендациям табл. 8.5.

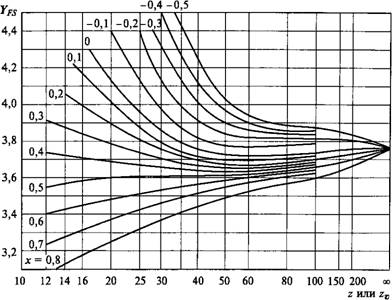
Из формулы (8.18) следует, что YFS — безразмерный коэффици­ент, величина которого зависит только от формы зуба (/', У, а^) И в том числе от формы его галтели (коэффициент К,). Форма зуба при одинаковом исходном контуре инструмента зависит от числа зубьев Z и коэффициента смещения инструмента х. Рассмотрим эту зависимость.

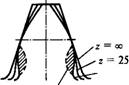
Влияние числа зубьев на форму и прочность зубьев. На рис. 8.21 показано изменение формы зуба в зависимости от числа зубьев колес, нарезанных без смещения с постоянным модулем. При z-> оо колесо превращается в рейку и зуб приобретает прямолиней­ные очертания. С уменьшением Z уменьшается толщина зуба у основания и вершины, а также увеличивается кривизна эвольвент - ного профиля. Такое изменение формы приводит к уменьшению прочности зуба. При дальнейшем уменьшении Z появляется подре­зание ножки зуба (штриховая линия на рис. 8.21), прочность зуба существенно снижается. При нарезании инструментом реечного ти­па для прямозубых передач число зубьев на границе подрезания Zmm = 17.

Функциональная зависимость коэффициента формы зуба YFS от числа зубьев Z хорошо просматривается по кривой х=0 на рис. 8.20. Yfs интенсивно уменьшается до za40 и далее остается примерно

Постоянным.

2= 18

Z<zn

Рис. 8.21

Рассмотренное влияние числа зубьев на прочность справедливо при постоянном мо­дуле, когда с увеличением Z увеличиваются и диаметры колес. При постоянных диамет­рах с изменением Z изменяется модуль т. В этом случае изменяются не только форма, но и размеры зуба. С увеличением Z форма улучшается, а размеры уменьшаются (уме­ньшается т). Уменьшение модуля снижает прочность зуба на изгиб [см. формулу (8.19)].

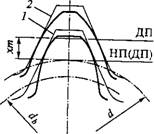
Смещение инструмента при нарезании зу­бьев и его влияние на форму и прочность зубьев. На рис. 8.22 изображено два поло­жения инструмента (рейки) при нарезании зубьев: 1 — делительная плоскость рейки (ДП) совпадает с начальной плоскостью (НП) — нарезание без смещения; 2 — ин­струменту дано положительное смещение Хт. При этом основной Db и делительный D диаметры колеса не изменяются, так как не изменяется Z (НП по-прежнему обкаты­вается по d, а ДП смещена на хт). Как видно из чертежа, смещение инструмента вызвало значительное изменение формы зуба. Толщина зуба у основания увеличилась, увеличилась и прочность зуба по напряжениям изгиба. Одновремен­но с этим заострилась головка зуба. Заострение является одной из причин, ограничивающих величину смещения инструмента. Отрица­тельное смещение инструмента сопровождается явлениями обрат­ного характера.

Применяют два типа передач со смещением:

1. Шестерню изготовляют с положительным смещением (хг>0)9 Колесо — с отрицательным (Х2 < 0), но так, что х{ | = х2 или Xz = хх + +х2=0.

При любом смещении сумма ширины впадины и толщины зуба по делительной окружности равна шагу р. Одинаковые по величи­не, но разные по знаку смещения вызывают одинаковые увеличе­ния толщины зуба шестерни и ширины впадины колеса. Поэтому в зацеплении зубчатой пары при делительные окружности

Соприкасаются и являются начальными, как в передаче без смеще­ния. Не изменяются также межосевое расстояние Aw и угол зацепле­ния <xw:

^=0=0,5 (</! + </2); а* = а=20°.

Рис. 8.22

Изменяется только соотношение высот головок и ножек зубьев.

2. Суммарное смещение хz не равно нулю. Обычно *е>0, а так - же Xi > 0 и х2 > 0. При положительных хх и х2 делительная толщина зубьев шестерни и колеса больше р/2. Поэтому делительные окру­жности не могут соприкасаться. Начальными становятся новые окружности, большие, чем делительные (Dwl>Dl9 Dw2>D2; см. рис. 8.4). Межосевое расстояние увеличивается:

Aw=0,5 (dwl + Dw2) >a = 0,5(dx + d2).

При этом увеличивается и угол наклона линии зацепления как общей касательной к основным окружностям, т. е. увеличивается угол
зацепления: aw>a=20°. Увеличение aw сопровождается уменьше­нием коэффициента перекрытия еа, что является отрицательным и служит одной из причин, ограничивающих применение больших смещений.

Нарезание со смещением позволяет во многих случаях повысить качество зубчатого зацепления. Применяя смещение, необходимо помнить:

1. Положительное смещение повышает прочность зубьев на изгиб и устраняет подрезание при малом числе зубьев (понижает z^). Например (см. рис. 8.20), при z=25 увеличение х от нуля до +0,8 уменьшает YFS в 1,2 раза. Соответственно уменьшаются и напряже­ния изгиба сf [см. формулу (8.19)]. В соответствии с табл. 8.6 можно понизить ZmШ от 17 до 8.

2. Увеличение aw при xz>0 повышает контактную прочность [см. формулу (8.10)]. Можно увеличить aw до 25° и поднять допускаемую нагрузку приблизительно на 20%.

3. При большом числе зубьев у шестерни и колеса смещение малоэффективно, так как форма зуба даже при значительных сме­щениях почти не изменяется. (У зубчатой рейки, которая подо­бна колесу при z= oo, смещение совершенно не изменяет форму зуба.)

Передачи со смещением при = 0 применяют при больших И и малых Zx. В этих условиях смещения хг>0 и х2<0 выравнивают форму зубьев шестерни и колеса и приближают их к равнопроч­ности по изгибу.

Таблица 8.6 Коэффициент Передачи Смещения Шестер­ни X, Колеса *2 Прямозубые Косозубые и шевронные 0 0 Z >21 0,3 -0,3 14<*i<20 Zi>Zmin + 2, но не менее 10 и и >3,5**. Реко­ Мендация не распространяется на передачи, у ко­ Торых Н2<350 НВ, а Hi —#2<70 НВ 0,5 0,5 Ю^г^ЗО*** ♦ Ограничение по подрезанию: Д град до 12 св. 12 до 17 св. 17 до 21 св. 21 до 24 св. 24 до 28 2пш 17 16 15 14 13 Д град св. 28 до 30 2тт 12 ** Ограничение по подрезанию: Д град до 10 св. 10 до 15 св. 15 до 20 св. 20 до 25 св. 25 до 30 Zmin 12 11 10 9 8 *** Нижняя предельная величина Z, определяемая минимумом еа= 1,2 в зависимости от Z2 Z2 16 18...19 20...21 22...24 25...28 29 Z 16 14 13 12 11 10

Смещения при х^фО могут влиять на большее число параметров зацепления. Рекомендации по выбору коэффициентов смещения да­ны в ГОСТ 16532—70. Некоторые из этих рекомендаций приведены в табл. 8.6.