Расчет прочности гибкого колеса
 5 февраля, 2013
5 февраля, 2013  admin
admin Варианты конструкции изображены на рис. 10.12. Расчетными являются размеры Ъ и <5, другие назначают по рекомендациям [17]: сЬ=dfg-2S, /^(0,7...1,0К — меньшие величины
При больших i; SI = S2=(0,9...0,6)S— меньшие величины при больших 8; ^=(0,15...0,25)6; Ъ2 — (0,3...0,5)6. Буртик уменьшает концентрацию напряжений на торце. Исполнение I — с гибким дном и фланцем для присоединения к валу; исполнение II — с зубчатым (подвижным) присоединением к валу или корпусу. Оба исполнения обеспечивают осевые перемещения при деформировании гибкого колеса (в противном случае имеют место большие напряжения). Возможны сварные варианты а, б, в. При выполнении указанных рекомендаций прочность гибкого колеса определяется сопротивлением усталости зубчатого венца.
Основные напряжения зубчатого венца:
1. Окружные напряжения изгиба генератором
<т,= Yz[ES/(2r2)] (w + d2wl&q>2).
|
B, b |
|
|
|
|
|
Исполне |
|
Щ |
|
Исполнение I |
|
- —J IM ^и^ДП" I нение |
|
Нение |
|
ТЩа Ш |
При деформировании по закону w=w0 cos 2q> напряжения изменяются по знакопеременному симметричному циклу с амплитудой (при ср = 0 и <р = я/2)
|
|
Аш =1,5 YzESw0/r2, (10.37)
|
|
|
Рис. 10.12 |
|
Б |
|
В |
|
Вал |
|
А |
Где Yz — коэффициент влияния зубьев: Уг« 1,35... 1,5 — зубья с узкой впадиной, Yz = 1,2... 1,3 — зубья с широкой впадиной (см. рис. 10.8). Большие Yz при f<150; г =(<4 +
+ <5)/2 — радиус срединной поверхности.
2. Напряжения растяжения от окружных сил в зацеплении, изменяющиеся по отнулевому циклу с максимумом при ср&О,
<гР«0,9 T2/(dJ>w6). Амплитуда напряжений и среднее напряжение цикла
3. Напряжение кручения
|
(10.38) (10.39) (10.40) |
Т=Т2/(2пг25), та = тт = т/2.
Кроме того, есть напряжения, связанные с нагрузкой зубьев как консолей и с прогибами зубчатого венца на шарах гибкого подшипника как дискретных опорах. Эти напряжения сравнительно невелики. Они выражаются сложными формулами. Поэтому в приближенных расчетах их учитывают путем некоторого увеличения коэффициентов запасов прочности.
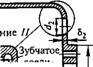
При проектном расчете внутренний диаметр гибкого колеса под зубчатым венцом определяют по приближенной зависимости, полученной из условия сопротивления усталости с учетом только напряжений at и <Тр [17]:
|
|
Коэффициентами фМ9 Yz, Sa задаются.
Фм=B/Dx « 0,15...0,2 — коэффициент ширины зубчатого венца (большие величины для больших / (> 150)); — коэффициент толщины зубчатого венца; Psd~ =0,012...0,014 для средненагруженных, длительно работающих передач (большие величины для больших /), 0,015...0,02 для высоконагруженных, кратковременно работающих передач; 5Ff«L,5...1,7 — коэффициент запаса сопротивления усталости; Xff = L,8...2,0 — коэффициент концентрации напряжений у ножки зуба.
Формула (10.41) позволяет выразить степень нагруженности передачи коэффициентом 4?Td=T2/d. Для отечественных и зарубежных редукторов общего назначения, которые можно рассматривать как средненагруженные, (0,2...0,3) • 106 Н ■ м/м3 — большие
Величины для 150.
Из материалов, указанных в табл. 8.7, для гибких колес чаще других применяют стали ЗОХГСА, Н«28...32 HRC, d_i = 420...440 МПа, при последующем дробеструйном наклепе =480...500 МПа; 40ХН2МА, Н«28...32 HRC, <7_!«480...500 МПа.
Для передачи с кулачковым генератором расчетный диаметр согласуется с наружным диаметром гибкого подшипника (табл. 10.1) поГОСТ 23179 — 78.
|
|
После определения диаметра рассчитывают все другие размеры гибкого колеса и выполняют проверочный расчет по формулам
(10.42)

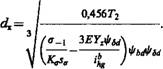
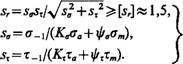
 Опубликовано в
Опубликовано в