Выше отмечалось, что методы определения индуктивности ка­тушек различных поперечных сечений без сердечников хорошо известны. Между тем расчет катушек с разомкнутыми ферромагнит­ными сердечниками связан со значительными трудностями и почти не разработан. Трудности расчета вызваны в основном наличием ферромагнитного тела ограниченных размеров в поле короткой ка­тушки. Формулы (2-18)—(2-20) позволяют приблизительно учесть влияние неподвижного сердечника на индуктивность катушки в слу­чае, когда катушка занимает симметричное положение относительно концов сердечника. В датчиках измерительных устройств это усло­вие не выполняется: под воздействием входной величины положе­ние феррита относительно катушки меняется В общем случае фер­рит только частично вдвинут в катушку. При движении феррита изменяется магнитное сопротивление потоку и распределение маг­нитных силовых линий поля катушки. Таким образом, каждому положению феррита соответствует вполне определенная картина поля, и расчет индуктивности датчика классическими методами ста­новится практически неосуществимым.

В конечном счете представляет интерес интегральный эффект, заключающийся в изменении индуктивности при перемещении сер­дечника. Предлагается метод, позволяющий произвести приближен­ный расчет датчика без углубления в структуру поля. Заменим ка­тушку эквивалентной схемой замещения, состоящей из двух после­довательно соединенных коаксиальных катушек, одна из которых имеет ферритовый сердечник, а другая не имеет его.

Пусть о>1 и (о2 — числа витков; 1Х и /2 — аксиальные размеры катушек (соответственно без феррита и с ферритом), причем

/1 + /2 = /кат; + =

Остальные размеры: dHар, ^внутр и толщина обмотки /кат — у обеих катушек одинаковы.

При изменениях входной величины, приводящих к изменению положения феррита, длины и числа витков катушек 1 и 2 также не остаются постоянными. Так, при вдвижении ст/ержня /j и wt уменьшаются, а /2 и w2 возрастают. При обратном движении стерж­ня картина изменения параметров меняется на противоположную. Суммарная индуктивность катушек 1 и 2 равна:

L — L-- L2--2M2.

Поскольку обе катушки примыкают друг к другу, нельзя не учитывать влияния ферритового стержня второй катушки на индук­тивность первой. Это влияние проявляется в увеличении индуктив­ности катушки 1 по сравнению с тем ее значением L01, которое

имело бы место при отсутствии феррита, и может быть учтено вве­дением некоторого коэффициента

В свою очередь на индуктивность катушки 2 влияет участок длины ферритового сердечника, выступающий за ее край.

Обозначив через Lm2 индуктивность катушки 2 с сердечником, длина которого равна длине катушки, запишем:

L2=Lmyk,2,

где k2>, a L2 определяется из соотношения

Для коэффициента взаимоиндукции М12 справедлива формула

Мм = 2 (^i+2

которая непосредственно следует из (2-38). Очевидно, что восполь­зоваться ей не представляется возможным, поскольку:

1) Li+2 — индуктивность катушки, составленной из катушек / и 2, в данном случае является конечной целью нашего расчета;

2) ввиду наличия ферромагнитного сердечника среда, в которой находятся катушки 1 и 2, не является изотропной. Область, занятая обмотками катушек и лежащая снаружи их, имеет магнитную про­ницаемость р-о*, эквивалентная проницаемость области внутри катуш­ки 2 равна » а внутри катушки 1 — &іЦо.

Для определения МХ2 воспользуемся искусственным приемам: заменим катушку с сердечником, находящуюся в среде с const, катушкой без сердечника. Последнюю будем рассматривать в среде

с магнитной проницаемостью ц0. При данном преобразовании необ­ходимо, чтобы Lu L2 и Afj2 остались без изменения.

Для того чтобы при произведенном преобразовании осталось неизменным значение М12, недостаточно выполнения этих условий. Необходимо, чтобы неизменным осталось и общее потокосцепление катушек. Последнее требование, очевидно, не может быть выполне­но со всей строгостью, так как картина поля новых катушек без сердечника в изотропной среде отличается от картины поля исход­ных катушек, находящихся в среде с лфconst и содержащих сер­дечник. Из сказанного следует, что предлагаемый метод нельзя рекомендовать для расчета картин поля катушек с сердечником.

В то же время при расчете интегральных параметров катушек он дает вполне удовлетворительные результаты, поскольку для слу­чая коротких и достаточно тонких катушек эта погрешность неве­лика, так как соответствующее увеличение эквивалентной плотности витков способствует примерно такой же концентрации магнитных силовых линий поля, как и при наличии ферромагнитного сердеч­ника. Кроме того, М12 входит в выражение для L в качестве одно­го из слагаемых.

1. Для получения максимальной чувствительности датчика при данных его габаритах витки катушки должны как можно блил£е примыкать к сердечнику. Поэтому увеличение диаметра катушки за счет с? Внутр, т. е. за счет удаления витков от сердечника, нецеле­сообразно, и во всех расчетах датчиков с катушками прямоугольно­го сечения полагаем */ВНутр~^с.

2. Наибольшие преимущества в схемах индуктивно-частотных преобразователей имеют датчики с отношением длины катушки к диаметру, близким к единице fJI. 34]. Сердечники коротких ка­тушек имеют отношение ljdt, равное нескольким единицам, и, следовательно, характеризуются значительной величиной размагни­чивающего фактора. В этих условиях для коэффициентов кх и k2 становится некритичным значение магнитной проницаемости мате­риала сердечника Оно может колебаться в пределах, соответству­ющих оптимальным значениям ц для рабочего диапазона частот индуктивно-частотных преобразователей (200—700 кгц).

Таблица 2-3 хорошо иллю­стрирует этот факт: при отноше­нии lddc = 2,5 изменение магнит­ной проницаемости материала в 2,5 раза изменяет коэффициент и, следовательно, индуктив­ность Lm только на 0,95%. Влия­ние же коэффициентов k и &2 на индуктивность меньше, чем влия­ние IV

Отношение tK/dK для кату­шек, используемых в датчиках индуктивно-частотных преобразователей, колеблется в небольших пределах. Экспериментальные исследования показали, что влияние его на ki и &2 можно не учитывать, так как оно соизмеримо с раз­бросом значений этйх коэффициентов, вызванным погрешностями

изготовления катушек и погрешностями эксперимента. Методика

определения коэффициентов k и k2 позволяет учесть изменение кар­тины поля катушек датчика при движении сердечника.

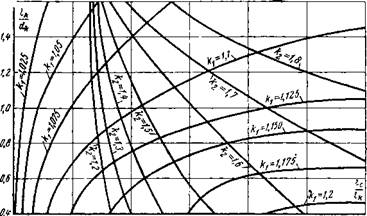
Значения коэффициентов k и k2 приведены на рис. 2-4. Пред­ложенный метод расчета может оказаться полезным при проекти­ровании индуктивных датчиков с разомкнутой магнитной цепью не только с катушками прямоугольного поперечного сечения, но и с профилированной обмоткой. В этом случае число слагаемых в (2-48) увеличивается в соответствии с количеством элементов, на которые будет разбита исходная катушка датчика. Точность метода ограничивается следующими факторами:

1) точностью используемых выражений для N/4n; Ф;

2) точностью определения поправочных коэффициентов kx и к2. В серии катушек, изготавливаемых для этой цели, неизбежны коле­бания lK/dK и tK/dK по сравнению с заданными значениями. Практи­чески индуктивность катушки рассчитывается с точностью до 3—5%.

Рассмотрим пример расчета индуктивности катушки с несим­метрично расположенным сердечником.

Исходные данные:

^к =~^с8 мм; 1■— 6 мм; І2~~2 мм; ^нйр = 5 мм; ^внутр~=4 мм; ^н = 4,5 мм; dc = 3 мм.

Марка феррита НЦ-600.

Вычисляем:

-4^-= 1,33; -4^—=0,442;

dK

Из рис. 2-2 находим: Фі (1,33; 0,221) = 4,6; Ф2 (0,442; 0,221) = 8,5; Ф-(1,78; 0,221) =3,76.