Как было указано в § 7.1, стандартную посадку выбирают по условно неподвижности соединения при заданной нагрузке без каких-либо дополнительных скреплений. Однако возможны случаи, когда намеченная посадка недопустима по условиям прочности сопрягаемых деталей, так как ее натяг вызывает их разрушение или чрезмерные деформации. Поэтому при расчете необходимо рассма­тривать как условие прочности (неподвижности) соединения, так и условия прочности его деталей. Расчет прочности деталей является проверкой возможности применения намеченной посадки.

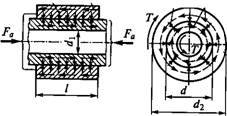
Расчет прочности соединения. На рис. 7.3 приведена расчетная схема соединения.

Условие прочности соединения при нагружении осевой силой

KFa^Fpndl, (7.2)

Где р — давление на поверхность контакта; 1,5...2 — коэффици­ент запаса.

Условие прочности соединения при нагружении крутящим мо­ментом

KT^Fpnd2!/!. (7.3)

При совместном действии Т и Fa

Ky/Ff+Fl^pndl, (7.4)

Где Ft=2T/D — окружная сила.

Л Pf

Р. Pf

Рис. 7.3

По теории расчета тол­стостенных цилиндров, изучаемой в курсе «Со­противление материалов», удельное давление на по­верхности контакта связа­но с натягом зависимо­стью

(7.5)

Где N ■

P=NI[D(CilEx + C2IE2)L Расчетный натяг; С и С2 — коэффициенты:

D2+d d2-di

D*+d1 Dl-d2

С,=

■flu C2 =

+ У-2,

Ei и Ei, Hi я ц2 — модули упругости и коэффициенты Пуассона материалов вала и втулки соответственно:

Для стали £«(21...22) • 10* МПа и /<«0,3, для чугуна £«(12...14)-104 МПа и /<«0,25, для бронзы £«(10...11)-10* МПа и /<«0,33.

(7.6)

При расчете прочности соединения расчетный натяг N определя­ют по минимальному табличному (JVmm) или вероятностному (Npmh) Натягу [см. формулу (0.1)] с учетом поправки и, т. е.

N=N(P)Min — U.

Величина и зависит от шероховатости посадочных поверхностей соединяемых деталей, способа сборки соединения и условий его эксплуатации. В общем случае

Здесь: UR — поправка на смятие микронеровностей в собранном соединении

UR = 1,2 (Rzl + Rz2) «5,5 СRai + R<a

Где i? zl, Rai — высота микронеровностей и среднее арифметиче­ское отклонение профиля посадочной поверхности вала соответст­венно; Rz2, Rca — то же для втулки. Обычно в посадках с на­
тягом поверхности обрабатывают по 6...8-му классам шерохова­тости.

Ut — поправка на температурную деформацию деталей. Она учи­тывает уменьшение натяга при эксплуатации за счет нагрева втулки или охлаждения вала, а также различие коэффициентов линейного расширения материалов соединяемых деталей.

Ut=d[(t2 - 20)а2 - (h - 20)а1]*,

Где T2, °С; а2,1/°С — рабочая температура и коэффициент линейного расширения материала втулки; Tx аг — то же для вала; D — диаметр посадки (рис. 7.3); а= 12 • 10"6 — для стали; а= 10 * 10~6 — для чугу­на; а=1910~6— для бронзы и латуни. Поправка Ut может не учитываться, если (T2—20) или (20 —не превышают 10 °С.

Ит — поправка, учитывающая уменьшение натяга в быстровра - щающихся деталях. Учет этой поправки актуален для соединений, работающих при высоких частотах вращения (свыше 20 000...30 0000 об/мин). Расчет ит см. [22].

Экспериментальные исследования показали, что величина коэф­фициентов трения на контактной поверхности зависит от многих факторов: способа сборки, удельного давления р, шероховатости поверхности, рода смазки поверхностей, применяемой при запрес­совке деталей, скорости запрессовки, наличия гальванических по­крытий и пр. Поэтому точно величина коэффициента трения может быть определена только испытаниями при заданных конкретных условиях. В приближенных расчетах прочности соединения сталь­ных и чугунных деталей при сборке нагревом рекомендуют: /=0,18 — при чистовом точении; /=0,32 — для оцинкованных и азотированных поверхностей; /=0,4 — для оксидированных по­верхностей; /=0,48 — при использовании абразивных микропорош­ков. В случаях сборки запрессовкой приведенные выше величины коэффициентов трения уменьшают в 1,8...2 раза. При сборке охла­ждением — увеличивают на 10%.

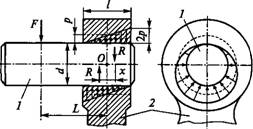
Изгибающий момент, которым может быть нагружено соедине­ние, определяют на основе следующих расчетов (рис. 7.4). Действие момента (M=FL) вызывает в соединении деталей 1 и 2 такое перераспределение давления р, при котором внешняя нагрузка урав­новешивается моментом внутренних сил MR=Rx.

Составляя расчетные зависимости, полагают, что поворот дета­ли 1 происходит вокруг центра тяжести соединения — точки О, а первоначальная равномерная эпюра давления (на чертеже показа­на штриховой линией) переходит в треугольную, как показано на рис. 7.4, или трапецеидальную. Кроме того, не учитывают действие

♦Температура окружающей среды принята равной 20 °С.

Силы F, перенесенной в точку О, как малое в срав­нении с действием момен­та М. Максимально дав­ление изменяется в плос­кости действия нагрузки. При некоторой величине нагрузки эпюра давления из трапеции превращается в треугольник с вершиной у края отверстия и осно­ванием, равным 2р. Этот случай является предельным, так как дальнейшее увеличение нагрузки приводит к появлению зазора (раскрытию стыка). Учитывая принятые положения, можно напи­сать

M=FL=Rx,

Где R — равнодействующая давлений на поверхностях верхнего и нижнего полуцилиндров. Величина этой равнодействующей опре­деляется давлением р посадки и не изменяется от действия изгиба­ющего момента:

R=Pld.

Плечо пары X=Lj3. Подставляя данные, получаем

M=Pdl2/3.

Для обеспечения необходимого запаса прочности соединения на практике принимают

M^0,2pdl2. (7.7)

При этом давление в наиболее нагруженных точках соединения не должно вызывать пластических деформаций.

Изменение эпюры давления, вызванное действием изгибающего момента, не отражается на способности соединения воспринимать осевую силу и вращающий момент, так как суммарная величина сил трения остается постоянной.

Рис. 7.4

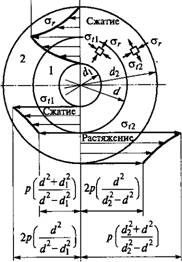
Расчет прочности и деформаций деталей соединения выполняют по формулам для толстостенных цилиндров. Эпюры напряжений в деталях 1 и 2 показаны на рис. 7.5, где ст — напряжение сжатия в радиальном направлении; <тг1 и ог2 — напряжения сжатия и рас­тяжения в тангенциальном направлении (осевые напряжения малы, их не учитывают). Давление р при расчете прочности деталей опре­деляют [см. формулу (7.5)] по максимальному натягу:

N=Nmax-UR. (7.8)

Приведенные зависимости спра­ведливы только в пределах упругих деформаций. Условие, при котором в деталях не будет пластических де­формаций (по теории наибольших касательных напряжений), таково:

(7.11)

<Тэх = <Т —

Где G — максимальное, а сг3 — ми­нимальное напряжения, считая рас­тяжение положительным; <тх — пре­дел текучести материала.

Нетрудно установить, что на­ибольшие эквивалентные напряже­ния <7Эг имеют место в точках внут­ренних поверхностей втулки и вала.

Для втулки сг1 = сг/2; сг3= —ог= —р И условие отсутствия пластических деформаций

(Dl+D> 2D

Или

P^°r2(d}-d2)/(2di), (7.9)

Где бгТ2 — предел текучести материала втулки. Для вала <Xi=0; сг3= — ап и оэх = с1и или

P^GTl(d2-dM2d2y (7.10)

Появление пластических деформаций не является во всех случаях недопустимым. Опыт применения посадок с натягом свидетельству­ет о том, что надежные соединения могут быть получены и при наличии некоторой кольцевой пластической зоны вблизи внутрен­ней поверхности втулки. Давление на поверхности контакта при наличии пластических деформаций можно определять по прибли­женным формулам:

При N^l,5NT p=pT(2NT-N)/NT;

Рис. 7.5

При N>L,5NT р=0,5рТ,

Где NT и Pr — расчетный натяг и давление, соответствующие пре­делу текучести.

Давление рт определяют как меньшее из двух при знаке равенст­ва в формулах (7.9) и (7.10). При известном рт по формуле (7.5) определяют NT.

(7.12)

Увеличение наружного диаметра втулки, вызванное растяжени­ем от посадки, можно оценить по формуле

A D2=2Pd2D2/[E2 (Dl - D2)].

Дополнительные указания к расчетам. 1. Приведенные выше формулы для расчета прочности деталей основаны на предположе­нии, что давление распределяется равномерно по поверхности кон­такта. Действительная эпюра давлений в направлении длины втул­ки представляется некоторой кривой, приближенный характер кото­рой изображен на рис. 7.6. Здесь наблюдается концентрация давле­ний (напряжений) у краев отверстия, вызванная вытеснением сжато­го материала от середины отверстия в обе стороны.

Эффект концентрации напряжений можно уменьшить изгото­влением деталей специальной формы. Примеры специальной формы вала и втулки показаны на рис. 7.7. Величина коэффициен­та концентрации напряжений Ка в соединении зависит от многих факторов: характеристик механической прочности материала, раз­меров деталей, давления, рода нагрузки и т. д. В качестве примера на рис. 7.6 и 7.7 указаны Ка при D= 50 мм, <тв=500 МПа, р^30 МПа.

2. Расчеты по наименьшему и наибольшему табличным натягам приводят в большинстве случаев к чрезмерно большим запасам прочности соединения и деталей [см. формулы (7.6) и (7.8)]. Так, например, для посадки 0 60#7/и7 (см. рис. 7.10 и пример расчета) наибольший натяг (105 мкм) в два с лишним раза превышает наименьший натяг (45 мкм). Во столько же раз могут изменяться действительные нагрузочные способности соединения и напряжения в деталях. Пределы рассеивания натяга уменьшаются с повышени­ем классов точности изготовления деталей.

Вероятность минимальных и максималь­ных отклонений размеров мала. Поэтому в массовом производстве выгодно применять вероятностные методы расчета, допуская ту или иную вероятность отказа (см. при­мер 7.1). В индивидуальном и мелкосерий­ном производстве целесообразно проверять расчет по измеренному натягу.

Так же как и в зубчатом соединении, в со­единении с натягом наблюдается коррозионно-
механическое изнашивание (фреттинг - коррозия), связанное с циклическими от­носительными микроперемещениями по­верхностей посадки (рис. 7.8). Нетрудно понять, что изгиб вала моментом М и кручение вала моментом Т распрост­раняются внутрь ступицы, как изображено на эпюрах М и Т. При вращении вала деформации изгиба — растяжения (+) и сжатия (—) — поверхностных слоев вала циклически изменяются (при по­вороте на 180° знаки меняются на обратные) и сопровождаются микросдвигами относительно поверхности ступицы. Кручение вала также вызывает микросдвиги, но в отличие от изгиба эти микро­сдвиги цикличны только при переменном вращающем моменте.

Изнашивание постепенно уменьшает прочность соединения и со­кращает срок службы.

Рис. 7.8

Расчет соединений с натягом на коррозионно-механическое изна­шивание пока не разработан, но известны методы снижения или даже устранения этого вида изнашивания: повышение твердости поверхностей по­садки; уменьшение напряжений с и т пу­тем увеличения диаметра в месте посад­ки; увеличение натяга или давления по­садки р, а следовательно, и сил трения, м которое сокращает распространение де­формаций внутрь ступицы и уменьшает относительные перемещения; образова­ние кольцевых проточек по торцам ступи­цы (рис. 7.8). Эти проточки увеличивают податливость ступицы, позволяют ей де­формироваться вместе с валом и умень­шают микросдвиги.