ПОЛНОЕ РЕШЕНИЕ ПРОБЛЕМЫ МОДЕЛИРОВАНИЯ
 18 ноября, 2013
18 ноября, 2013  admin
admin Если рассматривать шнек как последовательное соединение мфузочной, средней и выдавливающей зон и на этой основе попытаться вывести законы его моделирования с учетом переменно - ю влияния формующего инструмента, то сразу же возникает зат - тднение из-за жесткой связи между различными зонами шнека. >га связь делает невозможным такое положение, при котором каждая зона имела бы свое оптимальное число оборотов, опредс - ичпюе для нее на основе специальных (зональных) законов моде - шрования. Поэтому при определении размеров и режима работы шнека необходимо искать компромиссные решения. При этом в • |учас преимущественно теплопроводно-конвекционного нагрева получаются иные выводы, чем в случае выраженного автогенного I пособа работы.
Выше отдельные рабочие зоны шнека были охарактеризованы i юдуюшим образом:
I. Участок L\
1) с обогревом цилиндра и нейтральным шнеком;
2) с обогревом цилиндра и обогреваемым шнеком.
II. Участок Lj.
1) преобразование в тепло механической энергии без внешнего обогрева (автогенный режим работы);
2) превращение в тепло механической энергии с дополнительным обогревом.
Введение единой характеристики
Попытаемся охарактеризовать любой применяемый способ ра - оогы одним параметром, который позволял бы непосредственно определять долю теплопроводно-конвекционного нагрева в общем приросте энтальпии при переработке массы на шнековом
прессе. Мри этом будем исходить, например, из комбинации 1а/2а (участок Lj с обогреваемой стенкой цилиндра и нейтральным шнеком и участок L2 с преобразованием механической энергии без внешнего обогрева). В этом случае для чисел оборотов шнека N и № действуют следующие законы моделирования:
jDjD и JV2 = ;V2.о-
Компромисс между этими двумя различными положениями должен, по-видимому, ориентировочно выражаться в виде
|
|
|
|
а в общем случае — как
(2.14Х)
причем 0 < у < 0,5.
Если теперь определить коэффициент xj/ с гтомошыо уравнения
|
|
(2.149)
то получится, что крайнее значение j/ = 0 относится к случаю чисто автогенного способа работы (7"| = 7о), а величина у = 0,5 — к случаю чисто теплопроводно-конвекционного режима с обогревом цилиндра (Т = '/i).
За пределами применимости уравнения (2.149) для режима работы с обогревом цилиндра и шнека может быть принято у = 0,67.
Если скорость сдвига в случае D-шнека должна быть такой же, как в случае Д)-шпска, то необходимый для определения числа оборотов шнека компромисс между величинами /Vj и AS обязательно вызывает внесение соответствующих поправок в глубины нарезки А| и /»2 0-шиека.
Далее необходимо исследовать законы моделирования для числа оборотов N и глубин нарезки h и /ъ шнека, рассматриваемого как одно целое, а также вытекающие из них правила моделирования для характеристик мундштука К, давлений массы />, производительностей G, мощностей привода Ра и мощностей нагрева Р, г Это исследование относится главным образом к случаю комбинации 1а/2а. Другие случаи — 1а/2Ь, 1Ь/2а и 1Ь/2Ь — требуют только определенного изменения характеристики у.
Правила моделирования для случая комбинированного режима работы 1а/2а
В этом случае (участок Ц с обогреваемой стенкой цилиндра и неигральным шнеком, участок L-> с преобразованием в тепло механической энергии без внешнего обогрев;») для глубин нарезки
ека действительны уравнения (2.123) и (2.142).
Из компромиссного уравнения (2.148) между уравнениями (.’ 124) и (2.142), а также из требования о равенстве скоростей
• шита в случае /Минска и Д,-шнека непосредственно вытекают
• - к*дующие соотношения:
|
|
|
и |
(2.150)
(2.151)
)го является дополнительным подтверждением принятого в »учае 1а равенства величин компрессии для 0-шнека и Д>-шнека:
X = h//b =Л|.о/Л2.о=Хо-
|
|
(' учетом уравнения (2.151) можно также написать уравнение I онстанты мундштука (2.139) следующим образом:
(2.152)
Соответствующая настройка величины А'может быть дос гигну-
I. различными способами:
1) подгонкой длины мундштука (длины того участка, на котором поверхность формующего канала имеет параллельные образующие, — так называемой «длины обоймы»);
2) путем изменения ширины конического зазора между концом шнека и специальной вставкой (при этом либо сам шнек, либо iu инка перемешается в осевом направлении);
Ч установкой регулирующего вентиля между концом шнека и мундштуком.
На практике одна и та же машина почти всегда снабжается Формующими инструментами, имеющими весьма различные ха - р.1К1еристики, причем не всегда выполняется правило, приведенное в уравнении (2.152). Мри таких отклонениях становится неприменимым правило моделирования (2.148) для числа оборотов шнека, основывающееся на сохранении режима работы Д)-шнска I / V,,). В таком случае необходимо соответствующим образом из
менять условия работы 0-шнека (Та, /V). Если, например, характеристика больше, чем полагается по уравнению (2.152) (следовательно, сопротивление формующего инструмента меньше), то для 0-шнека следует повысить либо температуру 7'а, либо число оборотов N. либо обе величины вместе.
Правда, для обычных машин, которые работают с не очень большими числами оборотов, влияние константы К мундштука (по крайней мере, в случае шнеков, имеющих мелкую нарезку на выдавливающем конце) не имеет решающего значения.
Экструзия термопластичной массы через любой формующий инструмент, характеризуемый величиной К. происходит с производительностью Q. которая после подстановок уравнений (2.148),
(2.151) и (2.152), а также замены
|
|
|
Соответственно, получается следующее выражение для давления массы р: |
|
|
(2.155)
При адиабатическом способе работы (у = 0) и исполнении шнека, а также формующего инструмента в соответствии с правилами моделирования 0-шнек развивает такое же давление экструзии р, как 0(,-шнек. В случае же неадиабатического режима работы давление растет пропорционально (0/0о)4'. Это следует учитывать при расчете отдельных деталей формующего инструмента (дорно - держателя, болтов фланцевого соединения) на механическую прочность.
Автором работы |1| получены оптимальные значения угла подъема а и глубины нарезки /г.
|
|
|
sina(ormfM.) = 0,5, а(оптим.)- 30°
|
из которых следует, что
и
Интересно, что теоретические оптимальные значения И2 и и не ивисят от диаметра шнека. Величина И2 определяется только кои - i Iлитой формующего мундштука и длиной выдавливающей зоны шпека (кратностью диаметра), в то время как а для всех шнеков и формующих инструментов имеет одинаковую оптимальную величину (30°). Эти положения, конечно, справедливы в том случае, если термопластичный материал ведет себя как ньютоновский расплав.
Практически обычно работают с меньшим углом подъема вин - ювой линии, например 17*40', соответствующим шагу нарезки, равному 1/Л Угол подъема, равный 30°, был бы невыгодным для процесса продвижения гранулята или порошка в загрузочной юне, кроме случаев крайне низких коэффициентов трения между материалом и поверхностью шнека. С другой стороны, повышение угла подъема винтовой линии выше 17*40'лишь незначительно увеличивает производительность выдавливающей зоны, осо - «к-ино при больших сопротивлениях мундштука. Однако глубина нарезки при меньшем угле подъема винтовой линии должна быть оольше, чем при угле 30°.
В заключение этой части теоретического исследования рассмотрим требуемые дтя экструзии мощности привода и обогрева.
Мощность привода одношнекового экструдера рассчитывается in» формуле [1, 3, 4, 7J:
|
|
|
/?2 cos a 8tga |
|
|
|
. к - р'ср. Вероятно, частное от деления р'/S при очень малом зазоре 8 м<- к ту шнеком и цилиндром принимает предельное значение. Это |
При точных расчетах второй член в правой части этого уравнения требует корректировки, которая связана с тем, что в узком за - юре между выступами шнека и стенкой цилиндра расплав испы - | ывает особенно интенсивный сдвиг. Этот сдвиг вызывает (нспос - Р ICI BCHIIO или вследствие автогенного повышения температуры) < нижение вязкости расплава, находящегося в указанном зазоре. Кроме того, в наиболее общем случае нельзя принимать, что вяз - I «кть р остается постоянной на всем протяжении выдавливающей • ты. В данном_случае целесообразно применить среднюю величину вязкости р. Поэтому второй член в уравнении (2.157) следу - I разбить на сумму двух слагаемых с различными значениями ия jkocth:
относится практически как к автогенному, гак и к изотермическому режимам работы, поскольку описанный эффект не может быть полностью устранен ни при каких обстоятельствах. Разница между вязкостями в зазоре (ц') и в межвитковом объеме шнека (р'), вообще говоря, должна быть в случае изотермического способа работы больше, чем при адиабатическом режиме. Поэтому при изотермической работе обычно можно пренебречь уменьшением производительности, связанным с утечкой материала через зазор между выступами шнека и цилиндром. В то же время в случае адиабатического режима при определенных условиях с этой утечкой приходится считаться, несмотря на то, что при малом зазоре она очень мала но сравнению с поступательным движением материала и обратным потоком по межвитковому каналу шнека.
В дальнейших расчетах ограничимся упрощенным уравнением:
Ра = ^-D2 Mr2ptga + я2 Z>V2.-^2 . (2.158)
L h 2COSCX
Установлено, что если при переработке определенного материала заданным шнеком варьируется число оборотов N, то потребляемая мощность привода шнека изменяется в зависимости от условий работы. При этом, разумеется, не обязательно считать вообще постоянными давление Р в конце шнека и среднюю вязкость ц.
При изотермическом способе работы Р„ растет пропорционально числу оборотов шнека.
В случае изотермического способа работы получим 111:
Ра изотерм =СщЛ^2.
Отсюда следует, что в данном случае крутящий момент
изменяется пропорционально числу оборотов шнека N.
При адиабатическом способе работы требующаяся мощность привода в первом приближении может быть выражена соотношением j 11
^ииа6вСДЛ^,
в котором 1 < Д < 2. Отсюда следует, что крутящий момент
Л/</адиаб «СцЛН.
При более точном исследовании необходимо учитывать зави симость автогенного повышения температуры и, как результат, зависимость средней величины структурной вязкости Д от числа
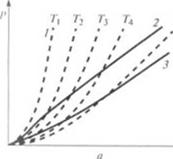
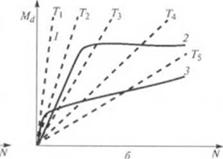
Iворотов шнека. Было найдено, что в случае адиабатического способа работы потребляемая мощность привода при малом числе оборотов шнека повышается пропорционально JV-, а при больших числах оборотов — пропорционально N. Следовательно, в данном случае крутящий момент на валу шнека при малых рабочих скоро - с |ях растет пропорционально v, в то время как при больших скоростях остается постоянным. На рис. 2.36 показаны потребляемая мощность и крутящий момент в зависимости от числа оборотов шнека при изотермическом и адиабатическом режимах работы, а 1лкжс для случая обычного режима работы (автогенный нагрев при одновременном теплообмене с окружающей средой постоянной температуры).
Если в уравнение (2.158) подставить выражение для N согласно уравнению (2.148), /»2 - согласно уравнению (2.151) и р — согласно уравнению (2.155), то получится:
|
3-чг |
|
|
|
+ -7jVo/l2.oA)^aO|J |
|
D А» |
|
,Nl «о |
|
Ра = пС2Д |
|
//2,о cos а |
пли
|
|
(2.159)
Для крутящего момента Md = PJN на основе уравнений (2.159) и (2.148) получается следующее правило моделирования:
|
3-2v |
|
3-2v |
|
л А |
|
I) 1А) |
|
= Л/, |
|
(2.160) |
|
|
|
N п |
|
|
Гис. 2.36. Записимосгъ погребной мощности Р{а) и крутящего момекта Мл (б) от чис - i. i оборотов А1:
/ при нютерми’кеком. 2 — при адиабатическом и 3 — при полигропном режимах рабо - 14 «> июшпекового экструдера
Как и уравнение производительности Q, уравнение мощности привода требует корректировки, если учесть, что некоторое преобразование механической энергии в тепловую имеет место также на участке L шнека и вследствие этого несколько уменьшается количество тепла, которое должно быть подведено от внешнего обогрева. В связи с этим повышается потребляемая мощность привода как в случае Л-шнека, так и в случае Дгшнека. Как это отражается на уравнении Ра =f(I)/D0), заранее сказать нельзя. Однако можно считать, что следствием автогенного процесса на участке Z, j, так же как и на участке Lj, будет повышение показателя степени у отношения D/Dq.
Правило моделирования потребляемой мощности обогрева можно вывести непосредственно из общего баланса мощности.
Баланс мощности шнекового пресса имеет следующий вид:
|
(2.161) |
где Р„ - подводимая мощность обогрева, включая покрытие потерь, кал/с; - потери мощности путем излучения, теплопроводности и конвекции, кал/с; с - средняя удельная теплоемкость массы в интервале температур от Т0 до включая удельную скрытую теплоту превращения. кал/(г • град); / = 42700 тс • см/кат - механический эквивалент тепла.
Произведением QP в правой части уравнения (2.161) по сравнению с тепловой мощностью Q{ Т — 7'nYfcl в большинстве случаев можно пренебречь.
|
|
Если теперь в уравнение (2.161) подставить
|
При условии, что машина имеет хорошую тепловую изоляцию и можно (при составлении энергетического баланса) пренебречь мощностью, расходуемой на выдавливание массы (не очень высокое число оборотов шнека или небольшое сопротивление мундштука), уравнение (2.163) упрощается и приводится к виду: |
|
|
|
а также значения Ра согласно уравнению (2.159), Q — согласно уравнению (2.154) и Я - согласно уравнению (2.155), то получится следующее правило моделирования мощности обогрева: |
(2.162)

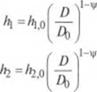
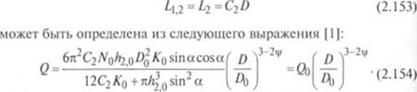
 Опубликовано в
Опубликовано в