Уравнения, следующие из II начала термодинамики
 18 ноября, 2013
18 ноября, 2013  admin
admin Второе начало термодинамики указывает на то, что внутренняя энергия системы состоит из свободной и связанной энергий. В самопроизвольном процессе освобождается только первая. Связанная энергия оказывается всегда тепловой энергией и при равновесных процессах равна 6Q = TdS, где 5 — функция состояния, называемая энтропией.
Свободная энергия может быть записана в различной форме. [Если в качестве независимых переменных (параметров) принять объем и температуру, то она имеет вид
W = W(V, T) = U — TS. (3.5)
,Если в качестве независимых переменных принять давление и температуру, то
0 = 0(p9T)=(/-TS + pV. (3.6)
Обычно функцию гР называют свободной энергией Гельмгольца, Ф — свободной энергией Гиббса или термодинамическим потенциалом Гиббса.
Для равновесных процессов уравнение (3.1) примет вид
TOC o "1-5" h z bQ = TdS=dU + bA. (3.7)
Отсюда
d¥= — SdT-ЪА, (3.8)
6Ф= - Sdr-M-f pdV + Vdp. (3.9)
Если 6/l=pdV', то = —SdT—pdV и dd> = —SdT+Vdp. Из
этих уравнений следует, что
|
|
Дальнейший термодинамический анализ высокоэластических деформаций делается для квазиравновесных процессов деформа- I ции. В этом случае применимы уравнения, аналогичные приведен - ] ным выше. Что касается неравновесных процессов деформации, то [их анализ относится к релаксационным явлениям и, в частности,. | к термодинамике необратимых процессов в полимерах.
|3.2.3. Квазиравновесные деформации сеточных полимеров | ТерхМодинамические соотношения (равенства) вполне строга применимы только к обратимым (равновесным) процессам. Поэтому термодинамические соотношнеия можно применять к полимерам. только в том случае, если обратимые деформации с достаточным [приближением осуществимы на опыте. Затруднения заключаются |в том, что в реальных условиях полимер подвергается действию различных химических процессов, приводящих к необратимому изменению структуры и свойств самого материала. При этом в одних {случаях химическими процессами можно пренебречь, а в других — [от них можно защищаться, но часто не удается сделать ни того,
ни другого, например в случае самопроизвольной (термической) деструкции цепей или узлов пространственной сетки.
|
|
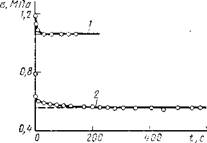
Хотя на опыте мы в той или иной степени всегда имеем дело с необратимыми процессами, из этого не следует, однако, что термодинамические соотношения нельзя применять для анализа экспериментальных данных. Например, когда действие химических процессов мало настолько, что допускаемые ошибки в результате пренебрежения этими процессами не превышают заданной точности, применение термодинамических соотношений возможно. Введение противостарителей подавляет химический процесс релаксации, и резина после физической релаксации (рис. 3.1) достигает стабильного напряжения.
|
|
Рис. 3.1 Рис. 3.2
Рис. 3.1. Кривые релаксации напряжения резин из натурального (/) и нат - рийбутадиенового (2) каучуков с противостарителем при 20° С и растяжении
100%
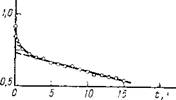
Рис. 3.2. Кривая релаксации напряжения резины из бутадиенового каучука при 90° С и растяжении 100%
Это говорит о том, что через некоторое время здесь достигается практически равновесное состояние. Экспериментально квазирав - иовесная кривая деформации обычно вычерчивается по отдельным точкам, получаемым из кривых релаксации напряжения при различных заданных деформациях.
В тех случаях, когда химическими процессами пренебречь нельзя, их можно учесть или исключить. Рис. 3.2 поясняет сказанное. Действие химических процессов здесь приводит к линейному падению напряжения. Экстраполяция этой линейной зависимости на ось напряжений дает условно равновесное напряжение, которое в отсутствие химических процессов было бы истинно равновесным, соответствующим неизменной структуре пространственной сетки резины. Следовательно, условно равновесное напряжение можно считать равновесным, отнесенным к неизменному начальному состоянию материала, и применять к нему термодинамические соотношения.
Термодинамические соотношения можно в отдельных случаях применять для полимерных тел с вязкотекучими свойствами. Деформация таких полимеров состоит практически из высокоэласти-
ческой и пластической составляющих, так как чисто упругой частью деформации можно пренебречь. В некоторых случаях удается обе составляющие деформации полностью разделить, например при установившемся режиме течения. В последнем случае к высоко - эластической составляющей деформации, зависящей не от времени, а только от приложенного напряжения, могут быть применены 'термодинамические соотношения.
Таким образом, термодинамическая теория высокоэластической деформации применима к высокополимерным телам в тех случаях, когда химическими процессами и текучестью можно пренебречь или исключить их каким-либо способом.

 Опубликовано в
Опубликовано в