Законы отражения и преломления ультразвуковых волн анало­гичны законам геометрической акустики.

Если продольная волна, распространяющаяся в некоторой сре­де I, встречает на своем пути среду II с другими акустическими свойствами, то часть энергии отражается от границы сред, а остав­шаяся часть входит в новую среду. При этом отраженные волны распространяются от границы раздела в первой среде, а прошед­шие — во второй.

Пусть плоская упругая продольная волна, распространяясь со ско­ростью Сі в однородной среде с плотностью pi, доходит до границы со второй средой с плотностью рп и скоростью распространения вол­ны в ней Си. Условимся углом а падения ультразвукового луча на­зывать угол, образованный лучом н нормалью к поверхности в точке падения луча.

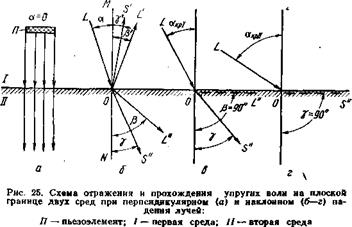
Если упругая волна падает перпендикулярно на плоскую границу раздела двух сред (а=0), то часть ее энергии переходит во вторую среду, а часть отражается в первую, причем проходящая и отра­женная волны будут того же вида, что и волна падающая, и направ­лены также перпендикулярно к границе раздела (рис. 25, а). Рас­пределение энергии между отраженной и прошедшей волнами опре­деляется коэффициентами отражения и прохождения.

Коэффициентом отражения R называется отношение интенсивно­стей отраженной и падающей волн. Для рассматриваемого случая

Я — (Рн си — Pi ci )/(Рц сн + Pi ci ), (1®)

где pi Сі и риса — удельные акустические сопротивления I и II сред. Если рцсц»рісі или рісі >рпсц, то Л» 1.

Коэффициентом прохождения D называется отношение интенсив­ностей прошедшей и падающей волн. Так как сумма коэффициентов

І

отражения и прохождения при нормальном падении равна 1, то ко­эффициент прохождения можно определить из уравнения

D= — R. (20)

Если продольная упругая волна L падает на границу раздела двух твердых сред под углом, отличным от прямого, то отраженная и прошедшая волны преломляются и трансформируются на продоль­ные L'L" и сдвиговые S'S" волны, распространяющиеся в первой и второй средах под различными углами (рис. 25, б; здесь для просто­ты показан всего один луч из пучка лучей). На практике для обес­печения падения продольных волн под углом между пьезоэлементом и контролируемой деталью располагают призму из органического стекла.

В этом случае угол а между падающим лучом 1.0 и перпендику­ляром MN к поверхности раздела в точке О называется углом па­дения; углы Р' и у' — углами отражения; углы р и у — углами пре­ломления (или углами ввода соответственно продольной и сдвиго­вой волн).

Законы отражения и преломления упругих волн по аналогии с законами геометрической оптики формулируются так:

1. Отраженные и преломленные лучи лежат в одной плоскости с падающим лучом и нормалью к поверхности раздела сред, проведен­ной в точке падения.

2. Угол отражения продольной волны равен углу падения.

3. При ріСі<рцСц углы падения, отражения н преломления свя­заны соотношением

sin а/спр1 = sin у7ссдв, - sin р/спрП = sin у/ссДв1Ь (21)

где спр і, спр и, Со дві и сс дВ и — скорости распространения продоль­ных и сдвиговых волн в I и II средах соответственно.

При увеличении угла падения а продольной волны L углы (I и у также увеличиваются и при некотором значении а=аКр і (первый критический угол) преломленные продольные волны распространя­ются по поверхности, не проникая в глубь среды II (рис. 25, в). При дальнейшем увеличении угла падения до аКр и (второй крити­ческий угол) по поверхности распространяются преломленные сдви­говые волны (рис. 25, г).

Для лучей упругих волн в полной мере справедлив закон обра­тимости илн взаимности: если луч падает из среды I на границу со средой II под углом а, преломляется и входит в среду II под углом Р, то луч, падающий из среды II на границу с первой под углом Р, после преломления войдет в среду I под углом а. Отсюда следует известное из оптики соотношение для относительных пока­зателей преломления обеих сред:

«12 = «i/«2 = 1 / «21 > (22)

где «і и «2 — абсолютные показатели преломления обеих сред.

Свойства упругих волн используют при конструировании наклон­ных преобразователей для контроля изделий сдвиговыми и поверх­ностными волнами. В них УЗК. преломляются с помощью клинооб­разной призмы, изготовленной из органического стекла, играющей роль среды I, а средой II является контролируемое изделие.

Зная скорость распространения УЗК в призме н контролируемом изделии, можно рассчитать значение углов распространения продоль­ных и сдвиговых воли в среде II в зависимости от угла а по фор -

муле (21). Так, например, на рис. 26 показан график зависимости углов у', р и v от угла падения а для призмы, изготовленной из органического стекла (спр. орг. ст.=2670 м/с, Ссдв. срг. ст.= 1120 м/с) и стали 40ХНМА (<?пр. стали — 5600 м/с, бсдв. стали— 3300 М/с). С ПО­МОЩЬЮ этого графика можно определить значения углов распрост­ранения отраженных и преломленных волн в этих средах в зависи­мости от угла а.

Рассмотренные случаи отражения и преломления лучей упругих волн справедливы только для плоских и гладких (зеркальных) по­верхностей соприкасающихся сред. Если поверхности раздела име­ют неровности, высота которых превышает 0,05—0,1 к, то наблю­дается диффузное отражение' и преломление, что приводит к иска­жению звукового поля отраженных и прошедших волн.