Назначение и методы моделирования процессов, протекающих в металле
 20 декабря, 2013
20 декабря, 2013  admin
admin При сварке различными способами происходит сложное взаимодействие разнообразных процессов, воздействующих на свариваемые детали. Основными из них, характерными для большинства способов сварки, являются:
• протекание электрического тока через сварное соединение;
• распространение теплоты от нагрева проходящим током и другими источниками, а также при последующем охлаждении;
• диффузия примесей, структурные, фазовые и химические превращения в металле шва и околошовной зоны, в том числе плавление и кристаллизация;
• деформация металла под действием как нагрева, так и других технологических факторов, приводящая к изменению его свойств, возникновению напряжений, а иногда к повреждению или полному разрушению.
Эти четыре фактора могут присутствовать и в эксплуатационных нагрузках, т. е. действовать на готовую конструкцию, влияя на ее работоспособность.
Таким образом, для оценки и повышения надежности сварной конструкции необходимо исследовать влияние на нее протекающих процессов. Основным современным средством такого исследования является проведение численных экспериментов на компьютерных моделях материала и процессов.
По сравнению с проведением обычных «натурных» экспериментов, компьютерное моделирование требует предварительных усилий для создания моделей в виде программного обеспечения. Однако в дальнейшем эксперименты на модели оказываются гораздо более оперативными, дешевыми и эффективными.
Эксперименты на металлических образцах остаются необходимыми для определения свойств материала, проверки модели, ее корректировки для решения новых задач, но за счет применения компьютерного моделирования они резко сокращаются по объему и сложности.
Рассмотрим методы моделирования процессов на примере решения задачи о протекании тока как наиболее простой для объяснения. Остальные из перечисленных задач сложнее, но решаются аналогично.
Постановка задачи такова: имеется сварное соединение, к нескольким точкам которого подведено напряжение от источника тока (потенциал этих точек известен). По детали течет ток, плотность которого различна в разных точках вследствие сложной формы и разного удельного сопротивления. Требуется определить значение плотности тока (как по величине, так и по направлению), а также электрические потенциалы в заданных точках на поверхности и в толще металла.
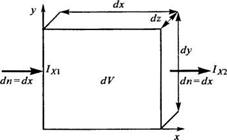
В простейшем случае (длинный ровный стержень из однородного металла) эта задача элементарна, но в реальных случаях сварных соединений дуговой и контактной сварки она чаще всего не имеет аналитического решения. К решению задачи возможны два подхода: опираться либо на дифференциальное уравнение, либо на интегральное. По своему физическому смыслу они аналогичны, различие имеет технический характер. Для задачи о протекании тока дифференциальным уравнением является уравнение постоянства заряда в элементарном объеме металла. Это уравнение справедливо, если рассматривать не переходные процессы при включении тока, а его равновесное, установившееся, медленно изменяющееся протекание. Для того чтобы заряд в элементарном объеме dV = dx-dydz (рис. 2.1) не изменялся, сумма токов, направленных внутрь элемента через все его границы, должна быть равна нулю.
Согласно закону Ома, плотность j тока пропорциональна напряженности поля Е, т. е. градиенту потенциала U:
|
(2.1) |
|
Рис. 2.1. Протекание тока в направлении оси* |
■ = }_Е = - р р дп
где р — удельное сопротивление вещества, п — координата, направленная по нормали к поверхности, через которую течет ток. Знак минус означает, что ток течет в направлении убывания потенциала. Ток равен произведению плотности тока на площадь поверхности, через которую он протекает. Суммар-
ный заряд, попадающий в элементарный объем dV через две его грани, перпендикулярные к оси х, пропорционален разности токов, протекающих через левую и правую грани:
|
|
Разность производных потенциала на двух гранях равна второй про-
d2U
изводной по координате х, умноженной на dx. Если —— > 0, значит ток,
дх'
втекающий через левую грань 1Х, больше, чем вытекающий через правую 1x2, т. е. в объеме происходит накопление зарядов. Всего по трем осям получаем
dq А дги 1 d2U 1 82U
■)dxdydz = 0.
dt рх дх2 р,, ду2 pz 8z2
Это уравнение постоянства заряда (первый закон Кирхгофа) приводит к уравнению Лапласа
|
(2.2) |
1 82U 1 82U 1 82U n
^r-0
рх дх2 рк ду2 pz 8z1
относительно потенциала произвольной внутренней точки. Его необходимо проинтегрировать по всему объему детали с учетом граничных условий, и эту задачу, как отмечено выше, редко удается решить аналитически, особенно если она нелинейна (если электропроводность неодинакова в разных точках тела, тем более если она зависит от плотности тока, т. е. от результатов решения задачи).
Интегральное уравнение можно получить из условия минимума энергии. При заданной разности потенциалов на границах тела выделение энергии при прохождении тока обратно пропорционально сопротивлению цепи. Ток течет по пути наименьшего сопротивления, совершая минимально возможную работу. Вся работа за единицу времени может быть найдена, если выражение закона Джоуля—Ленца проинтегрировать по объему тела:
P=j2pdV.
V
Равновесному состоянию соответствует такое распределение потенциалов и плотностей тока внутри сварного соединения, при котором значение интеграла минимально. Минимизируя Р, можно найти решение задачи. Трудности решения интегральных уравнений примерно такие же, как и дифференциальных.

 Опубликовано в
Опубликовано в