Для определения напряжения выделим в очаге деформации элемент с текущим радиусом (рис.20.4). Заготовка заталкивается в матрицу и стало быть в меридиональном сечении она испытывает напряжение. При обжиме диаметр уменьшается за счет экваториальных напряжений. При этом происходит удлинение элементов заготовки, и толщина не только уменьшается, но и увеличивается у среза дульца.

В результате давления на заготовку возникают: меридиональное напряжение , экваториальное , давление со стороны стенок матрицы и сила трения . Таким образом, деформированное состояние элемента при обжиме характерно трехосным сжатием.

Для определения величины действующего напряжения и усилия при обжиме составим уравнение равновесия.

На ось X:

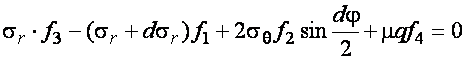(20.16)

На ось У:

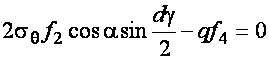(20.17)

Учитывая, что площади элемента равны:

; ; и

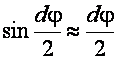И , а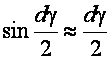

Получим: (20.18)

(20.19)

Так как 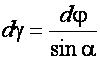, то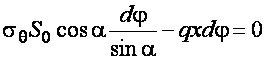

Откуда 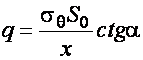(20.20)

Решая совместно (20.18) и (20.20), получим:

(20.21)

Интегрирование уравнения (20.21) при и граничных условиях когда ; дает:

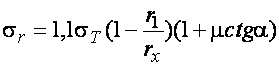(20.22)

При будет максимальным

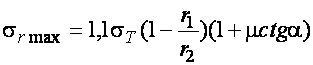(20.23)

Усилие обжима: 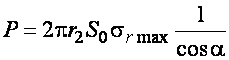(20.24)

Где 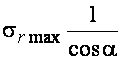- проекция напряжения на ось.

Или 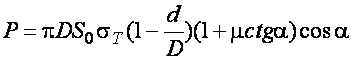(20.25)

/по Надаи/

Усилие обжима определяется также по формуле:

(20.26)

При обжиме в матрице с конической образующей усилие определяется по формуле Попова Е. А.:

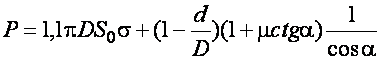(20.27)