Механизмы неньютоновского течения разделяются на две основ­ные группы [8]: активационные и ориентационные Механизмы пер­вой группы могут реализоваться и без разрушения структуры (ме­ханизм Эйринга, учитывающий, что энергия вязкого течения сни­жается с увеличением напряжения сдвига), но главным образом они идут с разрушением структуры и уменьшением энергии акти­вации (механизм Ребиндера [6.2], учитывающий, что для перехода от изменившейся структуры к исходной после снятия нагрузки тре­буется время тиксотропного восстановления). Время релаксации т процесса тиксотропного восстановления разрушений структуры ве­щества определяется [6.3; 6.4] соотношением

t=tmaxexpl—aexp(—b/v)]. (6.2)

Если входящие в (6.2) параметры принимают значения а = 0 или Ь-*-оо, то т равно максимальному времени релаксации ттах= = Тоехр[U/(kT)] системы в состоянии с неразрушенной структурой, т. е. может реализоваться только механизм Эйринга. В случае реа­лизации механизма Ребиндера аф0 и ЬФ0, что приводит к измене­нию т при переходе от покоя к процессу течения, наблюдаемому для разных веществ. Ориентационные механизмы структурной вязкости реализуются в системах, состоящих из анизотропных час­тиц вытянутой формы или из цепочек (полимеры). Для многих си­стем ориентационный механизм несуществен по сравнению с более мощным механизмом разрушения структуры.

Для объяснения природы неньютоновского течения системы, со­стоящей из кинетических единиц одного типа, Эйринг предложил уравнение, которое часто без достаточных оснований применяется и для полимеров в вязкотекучем состоянии:

т]=Лехр [U0l(kT) —=т,0—, (б. З)

shz sh z

где А — постоянная, зависящая от структуры вещества; параметр z=(d3P/(kT)—величина, прямо пропорциональная напряжению сдвига и элементарному объему юэ, приходящемуся на одну кине­тическую единицу течения. В области малых напряжений сдвига течение становится ньютоновским, так как при г<С 1 shz~z и

г] = const.

Физический смысл механизма, определяющего влияние напря­жения на вязкость, по Эйрингу, заключается в том, что энергия ак­тивации снижается с увеличением напряжения сдвига по некоторо­му закону. Это можно увидеть, если уравнение (6.3) представить в иной форме:

'П = Дехр[(6го~ ™BP)j{kT). (6.4)

Величина U—Uo—%соЭР — некоторая эффективная энергия актива­ции, зависящая от напряжения сдвига, а соэ — эффективный объем кинетической единицы, в роли которой может выступать атом, мо­лекула, коллоидная частица или сегмент макромолекулы. Параметр к в этом уравнении зависит от напряжения сдвига так, что при Р->0 он обращается в нуль, а при Р->оо — в единицу.

В механизме Эйринга не предполагается изменений структуры системы при переходе от покоя к движению, поэтому структурные параметры А и U0 в процессе течения считаются постоянными, но Р или dy/dt могут не только снижать {/, но и приводить к разру­шению структуры системы и снижать начальную энергию актива­ции и0 и динамическую вязкость г] тем в большей степени, 4tM больше скорость течения.

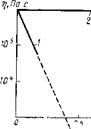
Процессы разрушения структуры отчетливо наблюдаются в тиксотропных дисперсных системах. В связи с этим важно срав­нить результаты, следующие из уравнения (6.4), с эксперименталь­ными данными. Известно, что сегменты макромолекулы, например эластомеров, содержат примерно 30—40 углеродных атомов в цепи главной валентности, что соответствует длине отрезка цепи 3,5— 5 нм. Так как расстояние между цепями в полимере примерно рав­но 0,5 нм, объем сегмента составляет (0,9-1-1,2) • 10-21 см3. Подста­новка характерного для полимеров объема сегмента (соэ= Ю-21 см3) в (6.4) приводит к выводу [6.5; 6.6], что уравнение не дает какого-
либо снижения вязкости в исследуемом интервале напряжений (кривая 2 на рис. 6.1). В этом интервале Р оказывается, что 1 и в формуле (6.3) г] = т]о — const. Снижение же вязкости, согласно Эйрингу, будет происходить при гораздо больших напряжениях Р, лежащих далеко за пределами измерений. Этот результат свиде­тельствует о том, что механизм Эйринга не объясняет зависимости вязкости полимеров от напряжения.

В реальных условиях в процессе течения структура полимера перестраивается. В случае механизма Эйринга структура в процес-

Рис. 6.1. Зависимость динамической вязкости Т] полиизобутилена при

353 К от напряжения сдвига Р:

1—эксперимент; 2—расчет по формуле (6 3) при (йэ=

= 10-21 см3 и ио=56 кДж/моль

се перестройки в целом остается той же (начальной), поэтому пос­ле снятия напряжения система должна иметь исходную структуру и физические свойства. В случае механизма Ребиндера структура изменяется и для ее возвращения к исходному состоянию после снятия нагрузки требуется время тиксотропного восстановления £г. в. Сразу же после снятия напряжения структура будет иной и лишь постепенно будет приближаться к исходной. С точки зрения явления тиксотропии механизм Эйринга относится к системам, у которых ^т. в = 0. В другом крайнем случае, когда это время очень велико, мы имеем дело с материалами, которые после разрушения структуры не способны ее восстановить.

Разрушение структуры может происходить по двум механиз­мам— энергетическому и энтропийному. Это разделение следует из общего уравнения в общей теории Эйринга — вязкости и диф­фузии жидкостей:

ц=А0 eFKk7")=A0 e-s/k (6.5)

где Aq — постоянная, равная ц при Т-^оо, F — свободная энергия, a S и U — соответственно энтропия и энергия активации вязкого течения. Первый механизм относится к случаю, когда при фактиче­ски неизменной 5 вместе с изменением структуры меняется и U. Этот механизм, предложенный Ребиндером [6.2; 6.4], характерен для дисперсных систем. Второй механизм, предложенный Бартене­вым [6.5—6.7], относится к случаю, когда при неизменной U вместе с изменением структуры изменяется и S. Этот механизм характе­рен для вязкого течения полимеров.

В случае энтропийного механизма при переходе в процессе раз­рушения надмолекулярных образований от упорядоченной к неупо­рядоченной структуре S возрастает. В частности, приняв для энт-
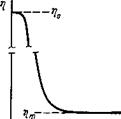
где ц0 = Вехр(и/кТ), B = AQexp(—S0/k) и а = |3/&; S0 — значение энтропии при напряжении сдвига Р — 0. Наличие аномальной вяз­кости у разнообразных конденсированных веществ может быть связано с различными причинами: 1) с тиксотропной структурой материала, когда имеется возможность обратного разрушения и восстановления связей между частицами; 2) с изменением формы

цепных молекул под действием напряжения, вследствие чего воз­можен переход от изотропной к ориентированной анизотропной структуре; 3) с разрушением цепных молекул полимера, приводя­щим к уменьшению его молекулярной массы.