При известных геометрических размерах соединения и натяге несущая способность в осевом и окружном на­правлениях определяется величинами контактного дав­ления и коэффициента тpeнияijTToдaвляющee большин­ство исследователей для определения контактных давлений в зависимости от натяга используют формулу Ляме. Существует единая методическая основа рас­чета, которой придерживаются и авторы настоящей работы. Вместе с этим использование формулы Ляме требует ряда уточнений, необходимость которых вызы­вается различными отношениями L/D у соединений, неодинаковой жесткостью охватывающей детали по длине, погрешностями изготовления. Отмеченные фак­торы влияют на действительную величину контактного давления, а это, в свою очередь, вызывает неточности при определении коэффициентов трения.

Экспериментальному определению коэффициентов трения посвя­щено большое «число исследований. Установлено, что они меняются в широких пределах в зависимости от материала сопрягаемых детален, способа сборки, давления, шероховатости, физико-механи­ческого состояния поверхностей н других факторов, вытекающих из молекулярно-механической теории трення [27, 28]. Рассмотрение многочисленных литературных данных показало, что единого метода определения коэффициентов треиия не существует, а это не позво­ляет в должной мере сопоставить результаты исследований и выя­вить действительное влияние различного рода конструктивных и технологических факторов. В настоящее время потребность в иссле­дованиях коэффициентов треиия заметно возросла. Это диктуется необходимостью повышения надежности изделий, расширением области применения цилиндрических н конических соединений с на­тягом, применением новых материалов и способов технологической обработки поверхностен, уточнением методов расчета соединений с целью снижения материалоемкости конструкций. Для объединения уснлнй и координации работ различных организаций необходимо разработать единую методику определения коэффициентов трения,
что исключит дублирование Исследований, будет способствовать их сравнительной ценности и достоверности.

Исходными зависимостями для - определения коэффи­циентов трения в цилиндрических соединениях яв­ляются: при передаче осевых усилий

U = (2-2)

/ос = (2-1)

При передаче крутящих моментов

2 Mv Nd4P

Достоверность оценки коэффициентов трения по этим формулам в основном зависит от точности опре­деления аргументов р, F. Погрешности геометри­ческих параметров, как величин низшего порядка, можно не учитывать. В этом случае, считая погрешности измерения р, F некоррелированными, средние квадратические отклонения коэффициентов трения определяют как при косвенном измерении величин (12] по формулам

После подстановки частных производных функ­ций (2.1), (2.2) получим

& = 2

'кр ndHp 1 Ndlp

S, _ 1

J/as + ^yss.

Здесь S-, S-, S - — средине квадратические отклонения результатов измерений величин давления, крутящего момента и осевого усилия, вычисляемые по формулам

S - _ SP ■ S = Sm ■ С _ Sp

Р W М Уъ' F~ У^'

Где Sp, SM, SF — соответственно средние квадратические отклоне­ния давления, крутящего момента н осевого усилия.

Доверительные границы изменения значений коэф­фициентов трения можно определить по распределению Стьюдента {12, 14] по зависимостям

/кр = /кр ± ^VSj ; /ос = /ос ± tv^f » 'кр 'ос

Где /Кр, /ос — значения коэффициентов трения, соответствующие средним величинам р, Мкр, F <v — дробь Стьюдента, определяемая из таблиц по доверительной вероятности и эффективным числам свободы, вычисляемых по формулам:

St + St(MKX,!Pr КЭф =------- ; j (скручивание);

S^+Si(F/Pr

К эф —--- J-------------------- J----------------- (осевой сдвиг).

Р

4+ „._ , SUF/Pr

Rip ---- I F Пр — I

При наличии одновременных измерений р, Мкр, F Точность определения коэффициентов трения может быть оценена по абсолютным величинам погрешностей, которые на основании теории ошибок представляют собой квадрат полного дифференциала функций (2.1), (2.2):

W V(AJ*+WVP)W; А/ос= - L - X

XV(Af)4(W(V,

Где А/нр, А/ос — абсолютные значения погрешностей коэффициентов трення прн кручении или осевом сдвнге^ Ам» Af, Ар — абсолютные значения погрешностей определения крутящего момента, осевого усилия и давления в соединении.

Оценка погрешностей измерения крутящих моментов или осевых сил особых трудностей не вызывает. Они определяются точностью испытательных средств или путем тарирования аппаратуры для измерения усилий. Как уже отмечалось, значительную сложность представ­ляет определение действительных значений давлений в соединениях. Неточности в определении р сказы­ваются на разбросах величин коэффициентов трения.

В большинстве работ при исследовании коэффициен­тов трения давления определяли расчетным методом по формуле Ляме, из которой следует, что погрешность в оценке давления зависит от точности определения
величины диаметрального натяга и размеров внешнего и внутреннего диаметров сопрягаемых детален. Обычно относительная погрешность измерения диаметров мала и влиянием ее на точность определения давления мож­но пренебречь. Тогда абсолютная погрешность оценки давления расчетным методом

Ар=± ЛДН> (2.3)

Где Дн — погрешность определения натяга в соединении;

Е

~ ~Т7г-------- />Т" — постоянный для конкретного соединения коэф-

А (сх + с2)

Фициент, Н/м'.

Составляющими величинами Д„ являются погреш­ности измерения натяга, величины смятия микронеров­ностей и формы. Наиболее значительными являются погрешности формы сопрягаемых поверхностей. Точ­ность оценки прочности соединений с цилиндрическими сопрягаемыми поверхностями зависит от того, каким образом учитывают переменную составляющую натяга. Если натяг определяется по наименьшим диаметрам сопрягаемых поверхностей (рис. 2.1), то действитель­ное среднее давление будет меньше расчетного. Следо­вательно, действительные значения коэффициентов тре­ния будут ниже найденных по формулам (2.1), (2.2). Если натяг определяется по наибольшим диаметрам (см. рис. 2.1), то из-за нецилиндричности сопрягаемых поверхностей действительные значения коэффициентов трения будут больше опытных.

Зависимость (2.3) справедлива для случая равно­мерного распределения давления (натяга) по длине

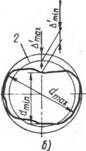
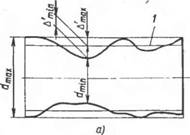
Рис. 2.1. Отсчет отклонений формы в продольном (а) н поперечном (б) сечениях от средней прямой 1 и средней окружности 2

Соединения. Поэтому погрешности Др следует рассчиты­вать по постоянному по длине приведенному отклоне­нию формы, которое вызывает такое же изменение сред­ней величины давления, как и действительные отклоне­ния формы. Приведенные отклонения формы можно определить, если за базы отсчета отклонений формы принять не прилегающие прямые или окружности согласно СТ СЭВ 301—76, а средние прямые или окружности, проведенные таким образом, чтобы пло­щади выступов и впадин реального профиля по обеим сторонам от линии были одинаковыми (см. рис. 2.1). За приведенное отклонение формы необходимо прини­мать большее из максимальных расстояний от средней линии или окружности до реального профиля продоль­ного или поперечного сечения цилиндра. Тогда погреш­ности определения натяга в соединении при расчете натяга

ПО Drain — Дн = 2 (Amin + Amin) При расчете натяга по

Dmax — Дн = [1] (Дгоах + А™*).

T я

Где Amini Дт1п—наибольшее расстояние от точек впадии реального профиля до средней прямой или окружности для охватываемой и охватывающей поверхностен соответственно; Лщах' Дщах— наиболь­шее расстояние от точек выступов реального профиля до средней прямой или окружности для охватываемой и охватывающей поверх­ностей соответственно.

Оценка натяга в соединении возможна также в виде разности средних диаметров сопрягаемых поверхностей, найденных по результатам п измерений [53]. В этом случае применима вероятностная оценка погрешности давления. Принимая измерения вала и втулки незави­симыми, получим [14, 53]: средние диаметры вала dB и втулки (JBt и их средние квадратические отклонения

I=l i=l f i=l /--------- ; ~

Средний натяг в соединении б

— <$вт ^ срсднсв КВ2Д-

Ратичное отклонение его SF = —Si + S„.

In

Степень точности

VII

VI

VIII

V

Интервал номинальных диаметров, мм

Предельное отклонение, ыкм

Свыше 10 до 18

По аналогии с зависимостью (2 3) среднее квадратич­ное отклонение давления равно Sp=ASs.

Степень влияния отклонений формы на точность определения коэффициентов трения зависит от номи­нального диаметра соединения. С уменьшением диа­метра влияние отклонений формы на несущую способ­ность соединений сказывается сильнее, так как для создания одних и тех же давлений требуются меньшие натяги, тогда как отклонения формы убывают в мень­шей степени, чем задаваемые натяги. Приведенные в табл. 2.1 предельные отклонения формы цилиндриче­ских поверхностей по СТ СЭВ 636—77 показывают, что при изменении диаметров от 18 до 250 мм допуски на отклонение формы увеличились всего лишь в 2,4— 2,6 раза.

Рассмотрим влияние отклонений формы на примере пяти соеди­нений с посадочными диаметрами, соответствующими предельным значениям интервалов номинальных диаметров, указанных в табл. 2.1. При этом, используя формулы (1.3) и (2.3), относительную по­грешность оценки давления представим в виде: До=Др/р=Дн/б. Величину б определим по зависимости (1.3), задаваясь конкретны­ми значениями давления и принимая валы сплошными (С,=0,7), а отношение D/D2=0,7 (С2=3,22).

Величину неточности определения натяга А„ примем равной удвоенному значению предельных отклонений от цилиндричноств (см. табл. 2.1), что соответствует случаям расчета давлений по наи­меньшему или наибольшему размерам сопрягаемых диаметров и симметричному расположению средней линии относительно впадии и выступов макропрофиля (см. рис. 2.1).

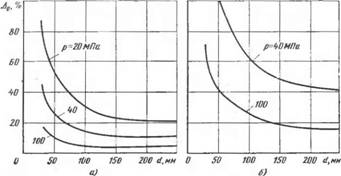
Результаты расчета относительной предельной погрешности оценки давлений при различных диаметрах соединения для пятой и восьмой степеней точности представлены на рис. 2.2. Погрешности оценки давления Д0 особо заметны при D<50 мм и р<40 МПа„

Рис. 2.2. Влияние отклонений формы сопрягаемых поверхностей, со­ответствующих пятой (а) и восьмой (б) степеням точности, на по­грешность расчета давления при разных его величинах и диаметрах Соединения

Когда величина отклонений формы соизмерима с натягом. При этом они в 2—3 раза могут превышать действительные значения давле­ний. При больших диаметрах и давлениях предельные погрешности До снижаются, однако остаются существенными.

Йз^изложенного следует, что методика исследования давлений и связанных с ними коэффициентов трения должна предусматривать определение их с учетом отклонений формы. В этом отношении заслуживает внимание расчет давлений по натягам, отсчитываемым от средней линии профиля. Однако при малых диамет­рах значительные погрешности и здесь не исключаются, так как переменная составляющая натяга зависит еще и от взаимного расположения профилей, учесть которое практически невозможно.

С целью повышения достоверности определения коэффициентов трения диаметры соединений опытных образцов, как показал анализ, должны быть (в зависи­мости от точности формы цилиндрических поверхностей) не менее 70—100 мм. Результаты многих исследований свидетельствуют, что с уменьшением размеров образ­цов разброс коэффициентов трения, как правило, увели­чивается. Так, в исследованиях [1] наблюдался полу- торакратный разброс коэффициентов трения в образ­цах с диаметром d = 48 мм. Такой же разброс коэффи­циентов трения наблюдался в однотипных образцах с диаметром cf=50 мм [8]. В работе [44] отмечается, что

2* 35

Разброс коэффициентов трения в образцах с d = 50 мм, формируемых тепловым методом, достигал 35%. В то же время минимальные значения их при распрессовке составили /р=0,12, тогда как на подобных образцах [1] получены коэффициенты трения fp=0,329 ...0,368.

Из приводимой в работе [44] подборки результатов исследова­ний следует, что рассеяние значений коэффициентов трения у раз­личных исследователей было различным. У Савина разброс коэффи­циентов трения при запрессовке образцов D=8... 210 мм составил fD=0.054 .0,22. Верт получил трехкратный разброс коэффициентов трения при распрессовке образцов d=5...30 мм, а именно fp= =0,086...0,25. В исследованиях Васильева разброс коэффициентов трения при кручении на образцах d= 18 мм достигал двух-трехкрат - нон величины. Между тем, у других авторов разброс коэффициентов трения для образцов d>100 мм не превышал 50%.

На погрешностях оценки давления в соединениях может сказаться сложная конфигурация образцов. В исследованиях [15, 51] определяли коэффициенты тре­ния при кручении в конических соединениях: для флан­цевого соединения среднее значение /Кр=0,18, для муф­товых соединений /кр=0,124 (в 1,45 раза меньше). Надо полагать, что это различие — результат повыше­ния давления в соединении под фланцем, что не учиты­валось расчетом.

Погрешности в оценке давления могут быть вызваны неправильным выбором соотношения длин сопрягаемых деталей. При выборе конструкции образцов необходимо учитывать, что длина вала должна примерно в 1,1— 1,2 раза превышать длину втулки. В этом случае по всей длине соединения созданы условия для равномер­ного распределения давления.

В конических соединениях непосредственное измере­ние натяга затруднено. Поэтому общепринято измерять его косвенным путем по величине изменения базорас - стояния (осевого натяга) в процессе сборки. Диамет­ральный натяг

6 = 25 tg а = SK, (2.4)

Где S — осевой натяг.

Точность измерения осевого натяга зависит от пра­вильного определения исходного положения сопрягае­мых деталей при их свободной сборке. С достаточной для практики точностью это можно установить для каждого соединения построением графической зависи­мости F=q>(S) путем ступенчатого приложения малых

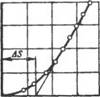
Рис. 2.3. Зависимость между осевым уси- F,HH Лием и осевым натягом в начале запрес­совки соединения с конусностью 1/50

4

Осевых усилий F к свободно со­бранному соединению и измерением 2 осевого натяга 5 (рис. 2.3). Опыты показали [4, 18, 51], что в началь- о Ofi О, в Hizs,Mn Ный период нагружения между F И 5 имеется нелинейная связь. Ее наличие объясняется особенностями контактирования шероховатых по­верхностей [ 17, 28]. При плавной сборке соеди­нений сопрягаемые поверхности в первоначальный мо­мент контактируют в нескольких точках. Под действием осевой нагрузки эти неровности сильно деформируются, и при этом происходят значительные относительные смещения деталей. С увеличением усилий в контакт вступает все большее количество неровностей, и вслед­ствие уменьшения напряжений на выступах микропро­филя интенсивность его деформации снижается, при­ближаясь к линейной зависимости. Основываясь на линейной связи между натягом и передаваемым уси­лием, вытекающей из зависимости (2.2), за исходное положение деталей следует принимать такое, начиная с которого прилагаемое к соединению осевое усилие вызывает пропорциональное изменение величины 5. Практически поправку AS для определения исходного положения деталей определяют продолжением линей­ного участка кривой F=<p(S) до пересечения с осью абсцисс (см. рис. 2.3).

Одна из особенностей контроля диаметрального на­тяга путем измерения осевого состоит в том, что даже при отсчете 5 от исходного положения контактирование сопрягаемых поверхностей происходит по вершинам микро - и макровыступов. В результате этого действи­тельный диаметральный натяг всегда будет ниже рас­считанного по формуле (2.4) из-за смятия микронеров­ностей, отклонения углов конусов и отклонения формы в окружном и продольном направлениях. Следова­тельно, в этом случае действительные значения давле­ний будут систематически завышенными, а величины коэффициентов трения — заниженными.

С целью повышения достоверности определения коэффициентов трения в работах [18, 24, 40] принят

Расчетно-экспериментальный метод определения давле­ния. Сущность его сводится к тому, что на внешней поверхности втулки измеряли окружные напряжения о<п, возникающие от посадки, и по ним определяли давле­ние на основе вытекающего из решения Ляме соот­ношения

[L-«w lt (2.5)

Tn 2 (d/d2)2

При этом напряжения измеряли тензометрическим методом. Тензодатчики соответственно главным напря­жениям располагали в двух направлениях: для регист­рации осевых &ZH и окружных е(п деформаций. Главные окружные напряжения определяли по зависимости

Ctn = , £„2 + Ш«п)-

Если тензодатчики тарировали по напряжению О=ЕЕ, создаваемому тарировочной балкой, то, считая модули упругости материала и балки одинаковыми, формулы для расчета главных напряжений будут иметь вид

^-^г^гК+Кп). (2-6)

» #

Где Atn и A^, — окружные и осевые напряжения от посадки, услов­но отнесенные к одноосному напряженному состоянию

Напряжения a'tn и о'т измеряли в процессе раз­борки соединений гидропрессовым способом, предвари­тельно формируемых с требуемым натягом. Учитывая, что гидропрессовый способ сборки и разборки обеспечи­вает сохранность поверхностей сопряжения, деформа­ции можно измерять многократно.

Распределение датчиков по длине соединения обес­печивает учет отклонений формы и уклонов, которые отражаются на характере изменения Ст(п. Влияние от­клонений поперечных сечений учитывается без дополни­тельных датчиков путем изменения перед сборкой взаимного положения вала и втулки в окружном на­правлении.

Для расчета давлений напряжения atn усредняли по количеству точек измерения и числу опытов. Точность определения напряжений и соответственно давлений оценивали методами теории вероятности. На основе теоремы о дисперсии суммы нескольких независимых случайных величин [14] среднее квадратичное отклоне­ние главного напряжения в i-ой точке, выражаемое зависимостью (2.6), определится по формуле

Sa — j/" W (o'ini) + p2D(o^)] , где D(a'int) И

D(o'zп() —дисперсии среднего значения напряжений в i-Й точке.

Половина доверительного интервала изменения сред­ней величины главного напряжения в точке = , где пр — количество измерений otni;

Tv — дробь Стьюдента.

Усредненные по длине соединения напряжения

Т

Ога= — , Otn.. где т — количество точек измерения Т jLJ 1

T=i

Напряжений. Тогда половина доверительного интер-

Вала измерения с<п составит До,_ = tv---------- ,

Т2у пр

Учитывая соотношение (2.5), среднее квадратичное отклонение давления, определяемое расчетно-экспери - ментальным методом

Т

S 1 I — (dldyf s

Р 2 (did,)» 2Lf V