Характеристики пластичности и прочности стыка в за­висимости от методов обработки сопрягаемых поверхно­стей, необходимые для расчета податливости стыка сое­динений с натягом, определяли попутно с описанными выше экспериментами по исследованию влияния техно­логических факторов на статическую прочность кониче­ских соединений при кручении.

На всех образцах (см. рис. 2.9) до проведения испы­таний статической прочности находили распределение моментов Mz по длине втулки и перемещения в стыке сопряженных поверхностей у свободного торца втулки. Распределение моментов определяли с помощью тензо - датчиков, наклеенных по схеме, исключающей влияние изгиба (см. рис. 2.11).

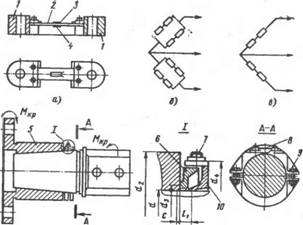
Для определения характеристик пластичности стыка был скон­струирован и изготовлен [39] датчик линейных перемещений (рис. 4.8). Датчик регистрирует деформации растяжения—сжатия упругого элемента 2, который при помощи захватов 1 жестко за­креплен на образце. Упругий элемент изготовляют нз материала, модуль упругости которого значительно ниже модуля упругости материала измеряемого объекта и деталей крепления. В данных опытах был использован текстолит толщиной 1 мм. Благодаря этому значительно снижается измерительное усилие и повышается точ­ность н чувствительность датчика за счет уменьшения касательных контактных деформаций в стыках деталей крепления упругого элемента на измеряемом объекте.

Деформация растяжения — сжатия регистрируется с помощью наклеенных на упругом элементе тензодатчиков и тензометричес - кой аппаратуры. Компенсация изгибных деформаций достигается наклейкой тензодатчиков по 4 боковым сторонам упругого элемента и соответствующей схемой их включения (рис. 4.8, б). В данном случае закрепление датчика перемещений обеспечивало его стабиль­ную ориентацию в одной плоскости, что позволило упростить схему включения (рнс. 4.8, в) и в качестве упругого элемента использовать пластину с двумя тензодатчиками 3, 4.

Датчик перемещений тарировали на специально изготовленном приспособлении (рис. 4.9), которое дублировало условия закрепле­ния датчика на образце. Этнм исключалась погрешность от дефор­маций деталей крепления под воздействием измерительного усилия. Масштаб записи определяли по величине электротарнровочного сигнала, величину которого устанавливали с помощью микрокато-

Ра типа ИГП ГОСТ 6933—72 с ценой деления 0,1 мкм. Погрешность замеров линейных перемещений не превышала 5%.

_ Установка датчика перемещений на образце показана на рнс. 4.8* г. На втулку 5 перед сборкой образца в непосредственной близости от внутренней поверхности с помощью винтов М4 на диа­метре Ds закрепляли кольцо 6. После сборки соединения на вал устанавливали кольцо 10, состоящее из двух половин, которые сое­динены болтами 9. На кольцах 6, 10 были приварены платнки, на которые с помощью винтов 7 на расстоянии d^2 от оси устанавли-

Вали Датчик 8 длй измерений малы* линейных перемещений. Кольца 6, 10 и закрепление прибора на образце были такими же, как и на тарировочном устройстве, что позволило исключить из за­меров деформации и перемещения в стыках промежуточных эле­ментов.

Так как датчик закрепляли на некотором расстоянии от исследуемого стыка, то он регистрировал общее пере­мещение Доб. которое наряду с перемещениями в стыке Д включало в себя упругие деформации втулки Двт и вала Дв. При этом Д=(Д0б—Двт—Дв) dfd^ где отноше­ние d/di служит для пересчета перемещений, измеряемых датчиком на диаметре di, к стыку, расположенному на диаметре D.

Круговая деформация втулки Двт на участке из — й была определена на основании выражения (4.10):

X2{<P-ddl- cPd3 + + d^l-dp

Ее наибольшая величина при максимальном хг и приня­тых конструктивных размерах составляла 0,69 мкм или 2% от величины измеряемого при этом перемещения в стыке. При обработке экспериментальных данных вво­дили поправку, учитывающую способ приложения кру­тящего момента М.

Деформация кручения вала на участке Л + с, соглас - А M(L,+C)D ,

Но теории кручения, Дв = — ' —, где ц — длина ва-

2GB/B

Ла между торцом втулки и серединой посадочной поверх­ности кольца 6 (см. рис. 4.8), определяемая для каждого образца (Л = 2,5 ... 4,2 мм); с — фаска на втулке (с= = 0,2 ... 1,0 мм). Величина Дв достигала 5—8% от зна­чения Д и учитывалась при обработке эксперименталь­ных данных.

Образец нагружали плавно, несколькими ступенями. На первой ступени величина крутящего момента при­мерно соответствовала упругому деформированию сты­ка. Образец нагружали не менее 3 раз. На ленте осцил­лографа одновременно фиксировались крутящие момен­ты М, Мг и перемещения Д0б в стыке при нагружении и разгружении соединения. На второй ступени нагрузку повышали до уровня, соответствующего появлению уча­стков локального проскальзывания, с последующей вы­держкой для стабилизации перемещения. На третьей

Ступени крутящий момент приближался к значению Мтах - Затем с образца снимали прибор для измерения перемещений в стыке и крутящий момент плавно увели­чивали до проворота вала.

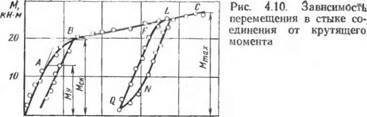
Результаты измерения распределения крутящих мо­ментов Mz обрабатывали общепринятым способом с уче­том остаточных крутящих моментов после предыдущих нагружений соединений, вызываемых локальным сколь­жением в стыке. По результатам обработки осцилло­грамм для каждого образца находили зависимость при­ложенного к соединению крутящего момента от смеще­ния в стыке, типичный вид которой показан на рис. 4.10. Выделяются три участка: ОА — практически прямоли­нейный участок, характеризующий упругое деформиро­вание стыка, А В — криволинейный участок, соответст­вующий пластическому деформированию стыка и ВС — Практически прямолинейный участок, отражающий по­явление и распределение зон локального проскальзыва­ния по длине соединения. Разгрузка соединения проис­ходила по линиям BE и LN, параллельным линии нагру­жения в упругой зоне. Если разгружение происходило на участке ОАВ, то стык упрочнялся и петли гистере­зиса не наблюдалось. В случае разгружения соединения на участке BLC вследствие перераспределения крутящих моментов между втулкой и валом из-за наличия участ­ков локального проскальзывания наблюдалась петля гистерезиса LNQF. Величина ее возрастала по мере при­ближения нагрузок к максимальным (точка С).

Из полученных экспериментальных точек составля­лось три выборки. В первую выборку объемом п вклю­чали точки на участке О А, во вторую, имеющую объем П2, включали точки на участке ВС. Эти две выборки за­тем аппроксимировали корреляционным уравнением пер­вого порядка. Некоторая субъективность в определении объема выборки практически не сказывалась на коэф­фициентах корреляционного уравнения. В третью выбор­ку объемом ri включали все точки и аппроксимировали корреляционными уравнениями третьего порядка. Кор­реляционные уравнения составляли по методу наимень­ших квадратов.

Корреляционные уравнения первого и третьего поряд­ков для выборок объемом п, щ и (П+п) соответственно имели вид

М = Ах + Л А; (4.30)

М = Cj + СзД; (4.31)

М = В + В1А+ Б2Л2 + В3 А3, (4.32)

Где А1, Л2, Си С2, В, Ви В2, В3 — коэффициенты, опреде­ляемые по известным зависимостям.

В наших опытах для корреляционных уравнений пер­вого порядка основная ошибка Ог'л не превышала 0,1 кН-м, критерий линейности £=0,001 ... 0,005, а его ошибка aЈi = 0,02 ... 0,03, что говорит о достаточно хо­рошей аппроксимации экспериментальных данных ли­нейным уравнением. Для корреляционных уравнений третьего порядка основная ошибка о23, < 25 кН-м, критерий кубичности £з = 0,002 ... 0,008, а его основная ошибка 0^3 = 0,03 ... 0,05, что позволяет считать аппрок­симацию экспериментальных точек кубичным уравне­нием достаточно хорошей.

Значения Му и Ду определяли из решения системы уравнений (4.30), (4.32), Мск и Дск — уравнений (4.31), (4.32). Учитывая значительный объем эксперименталь­ных данных более 200 образцов и громоздкость вычис­лений, коэффициенты корреляционных уравнений, их критерии и корни систем уравнений определяли на ЭВМ «Наири-С».

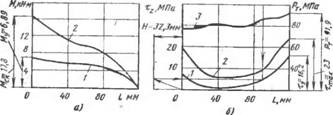
Для каждого образца строили распределение момен­тов по длине втулки для нагрузки М = МУ и М=МСК, Характерный вид которых показан на рис. 4.11, а. Кри­вая 1 соответствует упругому деформированию стыка, а кривая 2 — пластическому. Экспериментальные графики Mz=f(z) в последующем использовали для оценки кон­тактных касательных напряжений в стыке путем графи­ческого дифференцирования этой функции в соответст-

Вии с вытекающей из уравнения (4.4) зависимостью 2 dM2 v

Т, ==----------------- - . Характерный пример распределения

Л <Р Dz

Касательных контактных напряжений по длине соедине­ния представлен на рис. 4.11,6. Наибольшие касатель­ные напряжения возникают у свободного торца втулки при z=l. В середине сопряжения тг малы и соединение здесь практически не передает внешней нагрузки. У сво­бодного торца вала при z=0 напряжения тг несколько возрастают, но остаются меньше, чем при z=l. При z=l Касательные напряжения в первую очередь достигают сначала значений ту при М=МУ, потом тШах при М=МСК, а затем появляется локальное проскальзывание.

Коэффициенты касательной контактной податливо­сти при упругом деформировании стыка оценивали дву­мя способами: 1) определяли Кх из соотношения (4.2): /С*=Ду/ту; 2) путем решения уравнения (4.21), полагая Л1=Л1У; й2=Ду и z=l. Оба способа давали близкие ре­зультаты и за истинную величину Кх принимали сред­нее значение.

Согласно (4.3) коэффициент касательной контактной податливости при иластическом деформировании стыка

Дек —Ду

Атпл = ------------- —1

'шах ^у

При упругом и пластическом деформировании стыка коэффициенты трения находили по выражениям^ = 2l.

Fen — Тша* , где рг — давление на торце, рассчитан-

Рт

Ное по замеренному у торца посадочному напряжению atn в соответствии с зависимостью (2.5). Значение /ск начала появления проскальзывания сравнивали с при­веденными выше значениями коэффициентов трения, оп­ределенных с учетом действительного распределения давления в стыке при относительном провороте втулки и вала. Их различие не превышало 10—15%. Это свиде­тельствовало о том, что для выбранной конструкции об­разцов влияние краевого эффекта было незначительным.