Для корректной оценки параметров работоспособности конструкции необходимо не только выявление наиболее нагруженных зон исследуемого изделия, но и проведение детального анализа кинетики напряженно - деформированного состояния с учетом наличия локальных концентраторов напряжений, с последующей оценкой прочности и ресурса.

Для геометрически сложных объектов, состоящих из существенно разнотолщинных элементов, трудно за один этап решения оценить НДС не только конструкции в целом, но и отдельных, наиболее нагруженных зон, в частности сварных швов. Задача еще более усложняется, если приходится учитывать упругопластическое поведение материала на основе итерацион­ных алгоритмов,, так как при этом необходимо многократное решение сис­темы из многих десятков или сотен тысяч уравнений. В связи с этим эффек­тивен метод поэтапного расчета (МПР), обладающий высокой универсаль­ностью и позволяющий резко сократить вычислительные затраты.

Сущность МПР заключается в последовательном выделении подобла­стей со все более подробной детализацией КЭ моделей, при этом граничные условия для каждого этапа определяют по результатам предыдущего этапа расчета. На первом этапе проводится анализ нагруженности конструкции в целом от воздействия различных эксплуатационных нагрузок. При разра­ботке модели различные мелкие детали, не влияющие на ее глобальную же­сткость, могут быть опущены. На следующем этапе из этой модели выделя­ют наиболее нагруженные фрагменты и для каждого из них поочередно проводят более точный расчет. При этом каждый фрагмент разбивается на большее количество КЭ. При необходимости могут быть добавлены и вто­ростепенные детали, опущенные на предыдущем этапе расчета. Условиями нагружения фрагмента помимо усилий, приложенных непосредственно к нему, являются перемещения на его границах, определенные на предыду­щем этапе решения. После расчета и анализа нагруженности фрагмента от­дельные его зоны могут быть преобразованы в еще более подробные моде­ли, т. е. этапов расчета может быть несколько.

Имеется ряд программных комплексов, в которых реализован МПР. Как правило, этапы осуществляются для однотипных КЭ сеток, т. е. с пере­ходом от плоской модели к плоской, или от объемной к объемной. Однако на первом этапе анализа сложных листовых сварных конструкций наиболее эффектавны пространственные модели из пластинчатых КЭ с шестью сте­пенями свободы в узле, а для корректной оценки НДС в зонах сварных швов их использование неприемлемо. В этом случае необходимо применять объ­емные КЭ, имеющие три степени свободы в узле. Следовательно, нужен ал­горитм МПР с переходом от пространственной модели к объемной (здесь и далее под пространственными подразумеваются модели с использованием пластинчатых или оболочковых КЭ, а под объемными — с использованием объемных КЭ).

Результаты натурного обследования сварных конструкций показыва­ют, что наибольшее внимание при оценке прочности следует уделять зонам сварных швов, где помимо холодных и горячих трещин, связанных с техно­логическим процессом сварки или эксплуатационными нагрузками, сущест­вует повышенная вероятность образования трещиноподобных дефектов ти­па несплавлений, окисных пленок, подрезов, острых переходов от наплав­ленного к основному металлу. Такие дефекты характерны для всех видов сварных швов, но наиболее вероятны в угловых швах.

В реальных сварных соединениях наблюдаются случайные отклоне­ния сварного шва от идеальной формы, причем иногда в широком диапазо­не. Возможны различные дефекты. В довольно широких пределах изменя­ются физико-механические свойства сварного соединения, т. е. все сварные соединения являются неоднородными областями. Указанные явления при­водят к концентрации напряжений и снижению усталостных и прочностных характеристик соединения и определяют избирательный характер зарожде­ния трещин в участках с наиболее неблагоприятным сочетанием геометри­ческих и физических свойств. Степень опасности концентраторов различна и зависит от их относительных размеров, вида нагружения, свойств мате­риала. В общем случае задача еще более усложняется наличием остаточных напряжений и многоосностью напряженного состояния.

Использование МКЭ совместно с автоматизированным МПР позволя­ет рассчитать любую сварную конструкцию практически с любой требуемой точностью, вплоть до моделирования отдельных сварочных дефектов. Од­нако сам процесс моделирования дефектов довольно трудоемок. Кроме того, при оценках работоспособности сварного объекта, в связи со случайным характером расположения дефектов, их протяженности и формы, для доста­точной статистической представительности результатов требуется проведе­ние многочисленных расчетов, что значительно увеличивает трудоемкость работ по подготовке КЭ моделей сварочных дефектов. Поэтому для оценки работоспособности сварной конструкции при наличии сварочных дефектов, те или иные типы которых допускаются различными нормативными мате­риалами, логическим развитием МПР является вероятностная постановка задачи и использование алгоритма автоматической генерации дефектов, об­ладающих заданным комплексом характерных признаков.

Основным фактором, сдерживающим применение МПР, является вы­сокая трудоемкость определения граничных условий между этапами, свя­занная как с большим количеством передаваемой информации, так и со сложностью ее интерполяции на модель последующего этапа. В связи с этим необходима полная или частичная автоматизация МПР.

При решении реальных задач возможны различные типы перехода от этапа к этапу. Одним из наиболее сложных является переход от пространст­венной модели к объемной. Эту задачу можно условно разделить на две са­мостоятельные подзадачи:

1) преобразование угловых перемещений узлов пространственной мо­дели к линейным перемещениям соответствующих корневых (общих для предыдущего и последующего этапов) узлов объемной модели;

2) аппроксимация перемещений для остальных граничных узлов, до­бавляемых при дискретизации объемного фрагмента.

Первая подзадача связана как с отсутствием угловых степеней свобо­ды в объемной модели, так и с разнотипностью напряженного состояния в пространственных и объемных КЭ. Решение второй подзадачи необходимо для исключения разрыва сплошности полей деформаций по поверхности выделяемого сечения. Различные тестовые решения показали, что неучет этого фактора приводит к резкому искажению реальной картины НДС.

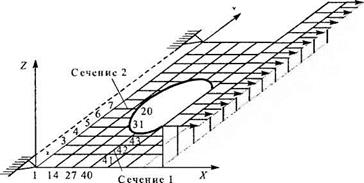
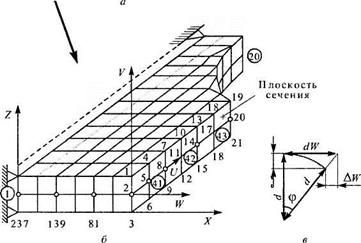
На рис. 2.16, а представлена модель 1-го этапа, состоящая из про­странственных КЭ, а на рис 2.16, 6 — выделенный из нее фрагмент, соот­ветствующий модели 2-го этапа, описанный в дальнейшем объемными КЭ. Показаны оси X, Y, Z глобальных систем координат обеих моделей, а также оси U, V, W местной системы координат первого подсечения первого сече­ния. Сечением 1 на рис. 2.16, а называется плоскость, проходящая через уз­лы 40—43, параллельная оси Z КЭ модель, а сечением 2 — плоскость, па­раллельная оси Z и проходящая через узлы 7, 20. Первое сечение включает в себя три стороны пространственных КЭ 40—41, 41—42, 42—43 и соответ­ственно в объемной задаче имеет три ограниченные области, называемые в дальнейшем подсечениями. Например, первое подсечение ограничено узлами 1—3—9—7 (см. рис. 2.16, б). Корневыми называются узлы КЭ модели 2-го этапа, соответствующие узлам КЭ модели 1-го этапа, но не лежащие на ней­тральной оси пространственного КЭ, например узлы 1,3, 7 и 9, но не 2, 8 и т. д. Обведенные кружками номера узлов на рис. 2.16, б соответствуют но­мерам узлов КЭ модели 1-го этапа.

Вектор граничных перемещений модели 2-го этапа рассчитывается в глобальной системе координат, но преобразование угловых перемещений в линейные возможно только с учетом реального расположения плоскости текущего КЭ модели 1-го этапа.

Реальное расположение плоскости текущего КЭ рассчитывается по координатам соответствующих двух узлов контура модели 1-го этапа и до­полнительного узла ориентации сечения, задаваемого в исходных данных.

Рис. 2.16. Пространственная КЭ модель 1-го этапа (а), выделенный из нее фрагмент объемной КЭ модели (б) и схема к пересчету угловых деформаций в линейные (в)

Для фрагмента объемной модели (см. рис. 2.16, б) в качестве узлов контура следует задать лежащие на оси пространственной модели узлы 2 и 8, а в ка­честве узла ориентации плоскости сечения — любой из не лежащих на оси узлов 1, 3,4,6, 7 или 9.

Преобразование угловых перемещений узлов модели 1-го этапа к ли­нейным перемещениям корневых узлов модели 2-го этапа осуществляется в соответствии с гипотезой плоских сечений. В связи с малостью деформаций, в зависимости от угла ср вычисляется только вектор dW (рис. 2.16, е) или аналогичный, добавки AV и AW не учитываются. Проведенные тестовые расчеты подтвердили их несущественное влияние.

Существенной является поправка, компенсирующая игнорирование деформаций по толщине листа в тонкостенных пространственных КЭ. Для ее внесения рассчитываются усилия, действующие по нормали к плоскости соответствующего пространственного КЭ и вызванные ими деформации объемного КЭ. Расчеты без этой поправки могут приводить к заметному ис­кажению НДС в одном или двух приграничных слоях объемных КЭ.

Исходными данными являются номера узлов моделей 1-го и 2-го этапов, принадлежащих сечениям, по которым выделяется модель 2-го этапа. Можно задавать не номера узлов, а только параметры секущих плоскостей с последующей автоматической выборкой соответствующих узлов. Это возможно в случае, когда сечение, по которому выделяется модель 2-го этапа, является плоскостью или поверхностью второго порядка.

Для аппроксимации перемещений промежуточных узлов необходимо установить закономерность изменения поля перемещений относительно по­верхности сечения. Так как в область сечения может входить различное ко­личество КЭ предыдущего этапа, то при реализации алгоритма коэффици­енты аппроксимации определялись последовательно, для каждой пары со­пряженных КЭ. При этом использован неполный полином 3-й степени, т. е. решалась система уравнений вида

Axf у і + Bxtyf + Сх - - г Dyf + Exiyi + Fxl + Gy + P = qt, (2.32)

где А, В, C, D, E, F, G, P — искомые коэффициенты уравнения аппроксима­ции перемещений; х,-, yt — координаты узлов, в которых рассчитаны ком­поненты перемещений <7/. Система уравнений была решена аналитически и получены зависимости для расчета коэффициентов уравнения (2.32) относи­тельно местной системы координат текущего подсечения.

Поскольку уравнения аппроксимации строятся локально (только для двух сопряженных подсечений), то в зонах сопряжения могут возникать разры­вы вследствие различия коэффициентов аппроксимации. Во избежание этого уравнения аппроксимации строятся с перекрытием по соседним подсечениям, а компоненты перемещений в зонах перекрытия усредняются. Подобный подход обеспечивает однородную, достаточно точную схему аппроксимации при раз­личной дискретизации пространственной модели 1-го этапа.

Координаты промежуточных узлов подсечения п + 1 в системе коор­динат U,, V, W н-го подсечения определяются после предварительного пово­рота плоскости подсечения п + 1 до совпадения с плоскостью и-го подсече­ния. Это обеспечивает возможность проведения выделяющего сечения по произвольной ломаной линии.

В реальных задачах, например при расчете сферических или цилинд­рических объектов относительно небольшого радиуса, может возникнуть необходимость выделения фрагмента по кривой. В этом случае промежу­точные узлы объемной модели могут не совпадать с гранью пространствен­
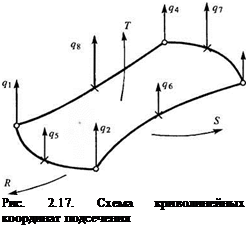
ных КЭ. Для аппроксимации перемещений по криволиней­ной области определяются на­правления осей криволинейной системы координат R, S, Т двух сопряженных подсечений по координатам их корневых уз­лов (рис. 2.17). Далее для каж­дого подсечения рассчитывает­ся матрица Якоби J, устанав­ливающая связь между производными по глобальным координатам X, Y, Z и по кри­волинейным координатам об­ласти R, S, Т:

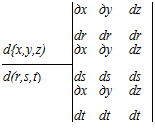(2.33)

В местной криволинейной системе координат R, S, Т находим коорди­наты узлов модели 2-го этапа для текущей пары подсечений

{r, s,t}T =J'{x, y,z}, (2.34)

где J 1 — обратная матрица Якоби. Далее по перемещениям корневых узлов в глобальной системе координат определяем перемещения всех узлов каж­дого подсечения

Qi = huqt + h2iq2 +... + hSiq&, (2.35)

где Qi — перемещение 1-го промежуточного узла подсечения; qx... q% — перемещения корневых узлов текущей пары подсечений; hu... — значе­

ния интерполяционных функций, рассчитанные для координат /-го проме­жуточного узла. Интерполяционные функции, соответствующие неполному кубическому полиному (2.32), могут быть записаны в следующем виде:

hjt = 0,125(1 + Л0)(1 + S0)( 1 + T0)(R0+ S0+T0-2) при j = 1, 3, 5, 7; (2.36)

= 0,25(1 - Л,2)( 1 + Su)( 1 + Т0) при j = 2, 6; (2.37)

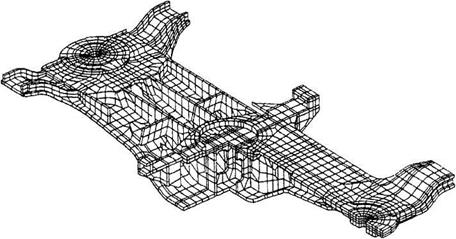
Рис. 2.18. Фрагмент КЭ модели штампосварной соединительной бал­ки четырехосной тележки восьмиосного вагона

hM = 0,25(1 - Sf)( 1 + 7?0)( 1 + Г0) при j = 4, 8, (2.38)

где R0 = R/RI: S0=S Sp, 70 = 7)7; R S;, Tj — значения координаты /-го

корневого узла; 7?,-, і',-, 7} — значения координаты /-го промежуточного узла.

Из задач поэтапного перехода с одинаковой размерностью наиболее сложным является переход от объемной модели конструкции к объемной модели ее фрагмента. Такие переходы необходимы для сокращения количе­ства параметров решаемой задачи.

На рис. 2.18 представлен фрагмент модели штампосварной балки восьмиосного вагона с 5744 объемными 20-узловыми КЭ и с более 100000 степеней свободы. Для оценки кинетики НДС в зонах сварочных дефектов данной конструкции необходимо дополнительное измельчение ее элементов как минимум в 6—8 раз по каждому направлению. Это приводит к увеличе­нию количества узлов модели и времени решения задачи на 2—3 порядка, что даже при учете мощности современных ЭВМ явно нецелесообразно.

Проблема перехода в том, что в модели последующего этапа количе­ство узлов на границах выделяемого фрагмента больше, чем в модели пре­дыдущего этапа. В связи с этим необходима аппроксимация перемещений на все узлы границы модели последующего этапа.

В алгоритме, реализующем данный тип межэтапного перехода в ком­плексе «АСТРА-С», обеспечено автоматическое определение номеров узлов моделей обоих этапов, попадающих в выделяющее сечение. В исходных данных задается только минимально достаточное количество номеров узлов, однозначно определяющих соответствующую поверхность. Далее по коор­динатам узлов модели и уравнению поверхности сечения определяются уз­лы, попадающие в сечение. Допуск Д на отклонение от поверхности задает­ся в исходных данных или определяется автоматически по эмпирической зависимости, учитывающей габаритные размеры моделируемой конструк­ции (А, В, С) и количество узлов модели (N):

А = 0,01 у](А2 + В2 +C2)7n. (2.39)

Для расчета граничных перемещений в узлах модели последующего этапа по их известным компонентам в узлах модели предыдущего этапа не­обходимо установить некоторый закон, в соответствии с которым возможно изменение поля перемещений относительно поверхности сечения. Как и при переходе от пространственной модели к объемной, целесообразно уравне­ния поверхности уровня компонентов перемещений строить не для всего сечения, а локально, для подсечений.

Каждое подсечение может содержать от шести до восьми узлов моде­ли предыдущего этапа. Поиск узлов подсечений осуществляется автомати­чески. Для этого, если выделяющее сечение — плоскость, все координаты узлов сечения преобразуются к системе координат секущей плоскости и ре­шается двумерная задача принадлежности точки многоугольнику (т. е. под­сечению). В случае криволинейного сечения по координатам узлов модели предыдущего этапа для каждого подсечения определяется своя криволиней­ная система координат R, S, Т. Далее для каждого подсечения рассчитывает­ся матрица Якоби J (2.33). Пользуясь зависимостью (2.34), находим коорди­наты узлов модели последующего этапа в местной криволинейной системе координат R, S, Т текущего подсечения. При этом для узлов, принадлежа­щих текущему подсечению, выполняется условие IR, £| < 1.

В случае, если выделяющее сечение состоит из плоскости или сово­купности плоскостей, для аппроксимации используется неполный полином 3-й степени (2.32) или полином более низкой степени при количестве узлов в текущем подсечении менее восьми. Для обеспечения непрерывности ап­проксимации строятся с перекрытием по соседним подсечениям, с после­дующим усреднением.

Если выделяющее сечение не плоскость, то для определения переме­щений в дополнительных узлах используется зависимость

Qi =КЯі +ІЬгСІ2 + ••• + hnClj’ (2-4°)

где q ... qj — перемещения в узлах модели предыдущего этапа (J = 6...8); hu. ..hji — значения интерполяционных функций, рассчитанные для коорди­нат i-ro промежуточного узла.

Интерполяционные функции могут быть записаны в следующем виде: h = gi(gs + gs); hj = gj(gj+ 4 + gj + 3) при j = 2, 3,4; hj = q при j = 5, 8; (2.41) gj = G(R, R.) ■ G(S, S.) ■ G{T, Ті) при j = 1, 8; (2.42)

G(P, P,) = 0,5(1 + P, P) при p,= ±1; G(P, ft) = (1 - p2) при p,= 0, (2.43) где P = R, S,T.

Разработанные алгоритмы автоматизированного межэтапного пере­хода были апробированы при решении тестовых задач и расчетах реальных сварных конструкций и показали удовлетворительные результаты.

Естественным развитием МПР является моделирование сварочных дефектов. Для оценки работоспособности сварной конструкции при наличии дефектов необходимы вероятностная постановка задачи оценки работоспособности исследуемого объекта и использование алгоритма автоматической генерации дефектов, обладающих заданным комплексом характерных признаков.

Весьма распространен дефект в виде поры или шлакового включения. В качестве признаков такого дефекта должен быть задан диапазон размеров (max, min), предполагаемая вероятность его возникновения по длине и глу­бине сварного шва, а также максимально возможное количество дефектов на длине L. Размер поры, ее форма и место расположения являются случайны­ми параметрами. Для генерации таких дефектов в модели использован сле­дующий подход.

1. Исходная бездефектная модель исследуемого сварного соединения описывается квадратичными 8-узловыми изопараметрическими КЭ.

2. Дефект моделируется в пределах одного КЭ модели. Если размер поры больше максимального размера дефекта, который может быть разме­щен внутри данного КЭ, то дефект моделируется в пределах нескольких смежных КЭ.

3. Место расположения дефекта определяется с использованием стан­дартного генератора случайных чисел.

4. Моделирование формы и размеров самой поры осуществляется ав­томатически по программе, построенной на следующих принципах.

4.1. Универсальная модель дефекта строится на области, обладающей 8 или 16 внешними узлами (под внешними узлами подразумеваются узлы исходной модели сварного соединения).

4.2. Универсальная модель дефекта включает фиксированное количе­ство внутренних узлов и квадратичных 8-узловых изопараметрических КЭ (рис. 2.19).

4.3. Основные относительные размеры КЭ внутри модели дефекта фиксированы в ее местных криволинейных координатах -1 < R, £| < +1.

4.4. Максимальный диа­метр поры в пределах исход­ного КЭ (или совокупности че­тырех КЭ) составляет 1/8 от стороны КЭ (или удвоенной стороны КЭ). Минимальный размер не ограничен.

4.5. 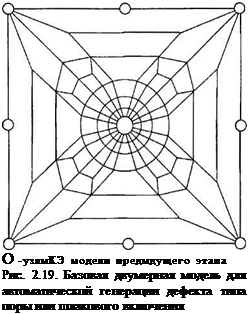Выбор условия мо­делирования поры на базе од­ного или четырех КЭ осуще­ствляется автоматически в за­висимости от абсолютных размеров текущего КЭ и мак­симально возможного размера поры — с/тах (заданного рас­четчиком).

4.6. Окончательная фор­ма и размеры моделируемой поры определяются автомати­чески следующим образом:

а) устанавливается базо­вый диаметр поры, равный 0,5с/тах;

б) на окружности, моделирующей базовую форму поры, устанав­ливаются четыре полюса, отстоящие друг от друга на 90° (или восемь полю­сов через 45° при необходимости моделирования более сложной формы);

в) по зависимости диаметра поры dn = 0,25dmax + Л определяется рас­стояние до каждого полюса, где А = (-0,25... + 0,25)(dmax - dmm ) . Значение Д из указанного диапазона выбирается автоматически с помощью генератора случайных чисел;

г) через полюса проводится кривая, являющаяся внешним контуром поры;

д) окончательные координаты узлов моделируемой области опреде­ляются из соотношений между декартовой и криволинейной системой коор­динат.

Таким образом, предлагаемая методика автоматически обеспечивает тре­буемую изначально степень неопределенности места возникновения и формы дефекта, которая при использовании данного алгоритма может изменяться от круглой поры до щелевидного или точечного дефекта. Особенностью данного алгоритма также является то, что окончательные расчеты ведутся на ограни­ченной области с заранее известными фиксированными параметрами, т. е. по­является возможность прогнозировать время, требуемое для проведения много­вариантных вероятностных расчетов с требуемой точностью.

Аналогичный подход использован при разработке универсальных объемных моделей дефектов сварных швов, а также при моделировании де­фектов типа подреза, наплыва и непровара корня шва.

При использовании разработанного методического и программного обеспечения возможно решение двух задач. В первом случае, если расчетчика интересует поверочная оценка ресурса конструкции и выявление параметров, определяющих изучаемый процесс, предполагается, что допуски на размеры того или иного типа дефектов известны, и при вероятностной обработке ре­зультатов расчетов фактически проводится поверочный расчет допустимости установленных нормативными материалами дефектов. Во втором случае реша­ется обратная задача, т. е. при заданном ресурсе конструкции устанавливаются закономерности влияния типа и размеров дефектов на ресурс и в результате определяются максимально допустимые параметры дефектов.