Метод конечных разностей или, как его еще называют, ме­тод сеток рассмотрим сперва на примере линейного распростра­нения теплоты в стержне, один конец которого поддерживается при температуре окружающей среды, а остальная поверхность теплоизолирована (рис.3.13). Этот случай имеет место, напри­мер, при контактной сварке двух стержней, концы которых же­стко зажаты в охлаждаемых медных зажимах.

Линейное оаспределение теплоты при постоянных теплофи­зических свойствах материала стержня описывается уравнением, аналогичны,: (3.2):

0Т ЭгТ 9t

Пусть в начальный момент t = 0 введена теїлота по из­вестному закону или, что то же самое, задано начальное рас-

х) ыхлее подробно см. Калиткин Н. Н.: Пислешше методы. - М.: Наука, 1978, глава XI.

пределение температуры

Т(х,0)=То(х) .

Пусть температура правого торца ( x=L ) постоянна: левый торец ( х = 0) теплоизолирован:

Ha one.3.13,а претедевы гладкие кр;геые, описывающие рпс - пределениз температуры в стержне в последовательные моменти

4-і і: 4.

Ретин теперь ту же. задачу методом конечных разностей. Метод основан на замене производных' их приближенны:.':.: значе­

ниями, выраженными через разности значенні: ь отдельны;; точ­ках - узлах сетки в отдельные моменты времени (рис.2. Г. б-- . Дифференциальное уравнение (3.20) в результате таких преоб­разовании заменяется эквивалентными сооїполлін. ти: ъ кеч:а

разностях.

Разобьем весь период нагрева и охлаждения на отдельные этапы. Пусть для простоты шаг сетки Ах постоянен, а вре - •денной промежуток между этапами к - ( и к равен At, т. е.

At = tK-tK_, . Тогда для узла x=LAx в момент t=tKH получим разностные отношения

вт/et»(TilK-T<.iK.,’)/At, ат/8ж«(тЫк.,-Ті,«-,УДх ■, (3.33)

та же производная слева от узла

эт/эос. Дх ,

^а*Ч(£Ы-'

_ Ты, к-1 ” 2-ТііК-д + Ті+11<_)

(йх)1

Здесь индексы указывают номера узлов сетки и моменты времени, Производные по х отнесены к предыдущему этапу, т. е. к мо­менту tk.(..

Подставляя выражения (3,33) в (3.30) и решая относитель­но Тс, к і получим

Ti, K=Ti, K-(+^^(rH, K-r2Tjill.|+Ti41l.,') . (3.31)

Аналогично могут быть получены формулы и в случае нели­нейной задачи, когда теплотизические свойства сварного со­единения К и ср непостоянны.

Граничные условия (3.32) в конечных разностях выражают­ся просто. Температура на правом торце на всех этапах прини - г. дается равной нулю: TH-K. i-T(L1t)=0 . На левом конце сетки вво­дится дополнительный узел (узел I я о на рис.3,13,6), кото­рый позволяет задавать нулевое значение производной путей выполнения условия Т0 к., =Т( для всех к.

Таси:.; образом, температуру в любом узле і в текущий ; п ;йг[; TL k можно найти но формуле (3.34), зная температу­ру •••їько в ото:- в двух соседних узлах в предыдущий мо - Начиная с момента t-At, когда к = I ;; Тік_рТ0(их)

•) v.-r. po'.io (3.31s, Процесс построения решения МОЖНО "Гро, иол—

как угодно далеко, если интервал времени fit удовлет-

воряет условию устойчивости решения

CL&t. J_

(Axf " 2. ‘

Физический смысл этого условия заключается в том, что при малом интервале времени &t на температуру в узле оказывают влияние только соседние уалы.

Принципиально так же могут быть по™ лучены формулы для расчета двумерного и трехмерного темпе­ратурного поля в сварном соединении любой формы с учетом температурной зави­симости теплофизи­ческих свойств ме­талла неоднородного сварного соединения, граничных условий, другого рода, допол­нительных источников и стоков теплоты и других факторов. На­пример, на рис.3.14,а на левой половине сечения симметричного стыкового соединения показана двумерная сетка с шагом Дх и &у. Формулу для расчета, температуры в узле і, j з текущий момент к можно получить аналогично формуле (3,34), 'введя дополнительную вто­рую производную по у :

ТІ, Ь і, кч +(д «н, і, к-1 гті, і, кН +

afit

х) См.: Калиткин Н. Н. Численные методы. - М.: Наука, 1978 с.373.

Условие устойчивости при Ах=Лу имеет вид

oat і

(Axf ' it ’

Таким образом в любой момент поверхность Т(х, у) ап­проксимируется совокушос/ы» точек Тцj (рис.3.14,6).

Здесь бнпа изложена так наанваемая явная схема. Ее ос­новное достоинство - простота; недостаток - ограничение на интервал времени At согласно уравнению устойчивости (3.35) и (3.37). Можно использовать также неявную схему, которая всегда устойчива, и интервал времени принимать большим. При неявной схеме производное по координатам х и у в (3.1) или (3.2) следует вычислять по значениям температуря в узлах сетки не в предыдущий момент кч, а в текущий момент к. Например, для одномерного случая аналогично (3.33) можно записать

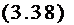УТ Т^.к - гЛЧ.)(+Т<.-н, к Эха (Ах)1

в результате чего получим основное уравнение для узла і :

+Qircf O'*"1 і к~ + ‘

/

n. At

► і строка

і строка

1

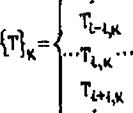
l W J L :

Легко убедиться, что непосредственна! переумножением I -й строки матриця [А] на столбец получается одно

уравнение (3.39). Видно, что матрица [А] симметричная, лен­точная, только на трех диагоналях элементы матрицы отличим от нуля. Поэтому решение системы с помощью вычислительных машин, например, методом Гаусса (для систем, структура кото­рых аналогична системе (3.41), он называется также прогон­кой) не представляет принципиальной сложности, даже если сетка имеет тысячи узлов.

Точность численного решения тем выше, чем меньше интер­валы Ах, А у и At, т. е. чем точнее аппроксимируется уравнение теплопроводности. Рекомендуется принимать мини­мальные значения &х и Ду в области высоких градиентов температурного поля (вблизи шва), a At в период высокой скорости изменения температуры.

Как следует из изложенного, основное достоинство метода конечных разностей - простота. Основной недостатком метода является следующее:

1) плохая аппроксимация криволинейной области прямо­угольной сеткой;

2) необходимость равномерного шага сетки, в противном случае очень усложняется расчетная схема.