Метод конечных элементов
 26 февраля, 2016
26 февраля, 2016  admin
admin Несмотря на то что метод конечных элементов развивается всего лишь немногим более 20 лет, он нашел широкое применение при решении сложных задач в разнообразных областях науки х) Более подробно см. [91 главы 3, 5, 8, 10» II.
н техники, в том числе в оварочннх науках. Метод конечных элементов лишен основных недостатков метода конечних равно - стой, хотя он намного сложнее и требует более мощных вычислительных машин.
Выбор метода ренення температурной задачи диктуется в основном методом ренення более сложной механической вадачн теории сварочных деформаций и напряжений. В главе 7 для ре - нения механической вадачи принят метод конечних елемвнхав кая более перспективний. Поэтому целесообразно достаточно подробно рассмотреть решение температурной задачи методом конечных элементов.
Основная идея метода состоит в том, что лмбув непрерывную функцию (температура, перемещение к т. д.) можно аппроксимировать куоочно-непрерывнига функциями, опредвлеяяши на конечної числе подобластей, вазяваемях элементами.
Проиллюстрируем основную идею на примере распределения температури в стержне (см. рис.3.13). Разобьем стержень на отдельные элементы 1,2.,...,е,.,Е, ограниченные двумя оо - оедними узлами і,2,...,і, і,...(рис, З.ІЗ, в). В пределах любого е-го элемента распределение температуры будем аппроксимировать прямой линией, причем точки н Tj однозначно определяют эту Прямую ЛИНИЮ, т. е. В любой момент tstK_4 функция Т(х) будет представлять собой кусочно-линейную функцию.
В двумерном случае тело разбивается на плоские конечные элементы в форме треугольника, которые связаны между собой тремя узлами (правая половина рис.3.14,а). Распределение температури в пределах элемента изображается теперь плоскостью (рис.3.14,б). Таким образом, в любой момент поверхность Т(х, у) будет апцроксимироватьоя совокупностью куоочно-пхоокнх поверхностей. Естественно, дня лучшей аппроксимация поверхности Т(х, У) в области высоких градиентов (вблизи шва) необходимо принимать плотность элементов наибольшей (наименьшие размеры элементов).
При построении дискретной модели двумерной области можно принять четырехугольники, а объемного тела - тетраэдра н параллелепипеды. Однако далее будем пользоваться только простейшими элементами: одномерными элементами о двумя узлами и треугольнши с тремя узлами, показаннши на рис. S.13,в и 3.14,а. Эти элементн прости в теоретическом отношении, я ими можно дискретизировать любое одномерное и двумерное тело.
Вернемся к примеру одномерного температурного ноля в стерине Сом, рис.3.13). В общем случае распределение температуры год мы не внаем, неиввестнн значения температуры в умах Т1Тгі...,Ті,>Т)1... . Нааа задача - найти их, причем так, чтобн последовательность значений Т,,Тг1... была бы наилучшш образом приближена к кривой Т(х), которая удовлетворяет одномерному уравнение теплопроводности. Это наидучвее приближение можно обеспечить, варьируя вое значения температуре в умах тан, чтобы минимизировать некоторый функционал*', которкй однозначно связен с дифференциальном уравнением теплопроводности.
Таким образом, последовательность определения температурного поля методом конечных элементов следующая:
1) оформулировать задачу теплопроводности, т. е. определить уравнение теплопроводности, начальные и граничные условия;
2) подобрать функционал, ..который обладает тем свойством, что функция, при которой он отановитоя мннимальаш, удовлетворяет как походному дифференциальному уравнению теплопроводности, так н граничним условной;
3) разбить несла дуемую область на алементя (днелретнзи - ров&ть облаоть) н выбрать функции, аппрохоимнрувиие неконое температурное поле в пределах каждого елемента;
4) выразить функционал через значення температури в узлах элементов;
5) продифференцировать функционал по каждому неизвестному значенню температури в узлах к производные приравнять нулю;
6) решить полученную систему уравнений относительно неизвестных значений температури в узлах.
Основная часть параграфа и будет посвяцена всем этапам решения этой вариационной задачи.
Захяж моментом метода конечных элементов является по-
х) Если числам х ставятоя в соответствие числа у, то дана функция - у*5(х) ; если функциям f ставятся в соответствие числа X, то задан функщюках, например, в случае функции двух першої
отроение интерполяционна! функций, которве в пределах каждого элемента аппроксимируют искомое температурное пахе. В качестве такой функции возьмем полином первой степени. йяряяни его через значения в узловых точках.
Дхя одномерного элемента (ом. рис.3.13,в) функция Т имеет вид
Т^^-Цх. (3.42)
Коэффициента лі и Лг определяются о помощью условий в узловых точках і и j :
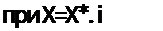 Т=Ті
Т=Ті
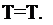 при x=Xj.
при x=Xj.
Подстановка-этих условий в формулу (3.42) приводит к оиотеме уравнений
TV^+oLjXi,
ремая которую получим
, „TtXi-TjXi
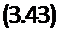 —V *— Л «ІіЛ
—V *— Л «ІіЛ
I т
где.
Подставляя значения Лі я Лг в уравнение (3.42), имеем
t і
ДЛЯ В ЯруГОИ ВЯД6
+ і. (3.44)
Это уравкение зашгаеы в матричном виде
Т-МЛ+М^-МЙ > <3.45)
где - матричная строка; функция Nt,, N, назы
ваются функциями формы
і к|—^^(л—Л|,^ .
 Дхя функций формы характерно то,
Дхя функций формы характерно то,
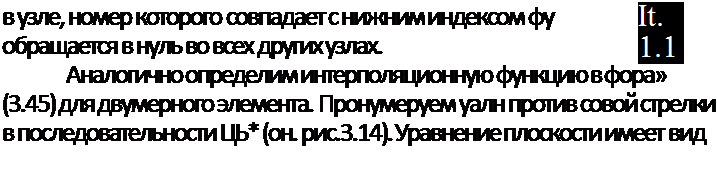 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
![]()
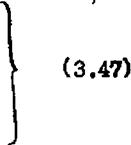
ai”Xi>K XK? J 1
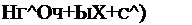 ЪПГ'Ь »
ЪПГ'Ь »
Я* і
![]() аГ^і"^кЧ,
аГ^і"^кЧ,
ЬГКк-Vi, сґхгхк ;
ак=хі. Т/І.“^0і , V4i-*j,
Чвхі“*і ’
Сформулируем двумерную вадачу теплопроводности в дифференциальной форме с более полеш учетом условий сверни* чем ято делали до сих пор.
Нестационарное уравнение теплопроводности имеет вид
CPdt"вхСх9*Г fyV * 9* )
где А. х, Ц - коэффициенты теплопроводности в направлениях х ш у ; й ~ удельная мощность источника (стока) теплоти внутри тела (Вт/М3); ср, , а могут бить функциями X,
^ и t, т. е. тело может быть разнородным и его свойства зависят от температура. Уравнение применимо как в изотропнш ( Хх=>^ ), так и к анизотропнда ( ) телам.
Начальное условие ( t * 0)
![]() T(x,^0)=To(x, y) .
T(x,^0)=To(x, y) .
Граничные условия:
а) на части граничной поверхности S, выполняются условия
![]() ^El**S!7'-rV-LT(^T_>'0 ;
^El**S!7'-rV-LT(^T_>'0 ;
б) на части граничной поверхности Sa заданы значения температуры
![]() Т=Т. ; (3.53)
Т=Т. ; (3.53)
объединение и Ьг образуют полную границу Ь. Здесь 1Х * Ц - налравляпцие косинусы вектора нормали в поверхности;
<V - удельная плотность теплового потока на поверхности S< (положительна, если теплота вводится), Вт/м2; «1т- коэффициент теплообмена; Тм - температура окружающей среда. Боли на границе Si обе величины и о£т равны нуле, то равенство (3.52) сводится к условию
^■жЭх» (3.54)
что отражает отсутствие теплопереноса через границу Si. В случае изотропного тела последнее условие можно записать в виде
“О, (3.55)
Эп 1
где п - нормаль к поверхности.
С! практической точки зрения задача СЗ.50)—(3.53)является достаточно полной для описания тепловых процессов при
сварке. Например, с помощью объемного источника Q. можно
моделировать ввод теплоты через наплавляемый металл, выде - лящуюоя теплоту при прохождении электрического тока, окритую теплоту плавления и кристаллизации и т. п. При рассмбтре - нии половины симметричного сечения стыкового соединения (ем. рис.3.14,а) граничным условием (3.52) можно описать теплоотдачу ( q, = 0, aLf> G) на поверхности BCDE и 0F и теплоизоляцию ( <v = 0, J. T= 0) границы ОАВ. На достаточно удаленной от шва АБСА условной границе EF можно задать условие (3.53), рассчитав температуру по аналитическим формулам, например по формуле (3.16); исходите величины 0. , ^ ,<АТ, ,
Тъ и поверхность могут изменяться в процессе сварочного нагревр и охлаждения. Хотя свариваемое изделие, как правило, считается изотропиям, далее будем коэффициенты А. х и Х.^ различать, с тем чтобы сохранить единство формы записи решения задач теории теплопроводности и теории термопластичности.
Уравнение (3.50) вместе с краевши условиями (3.51)— (3,53) однозначно определяет задачу. Оно служит отправной точкой для решения задачи методом конечных разностей. Метод конечных элементов основан на вариационном подходе. В вариационном исчислении устанавливается, что решение уравнения (3.50) с граничными условиями (3.52), (3.53) эквивалентно
 |
отысканию минимума функционала*^
+ 5KT+TeLTtT"T-')a]<ls ■ (3.56)
S
Все параметры уравнения (3.50) и граничные условия (3.52) содержатся в (3.56). Начальные (3.51) и граничные условия (3.53^ учтем позже.
Такое распределение температуры Т, при котором функционал Х(Т) становится минимальным, является решением походной задачи. Минимизируем его, используя множество аппроксимирующих функций, каждая из которых определена на отдельном элементе и выражена через значение в узлах. Так как узлов ыз значения определяет величину функционала, то минимизация и должна быть проведена по этим значениям. С этой целью разобьем интегралы (3.56) по отдельным элементам и в пределах каждого элемента распределение температуры Tte1 выразим через ее значения в узлах [Т] :
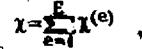 (3.57)
(3.57)
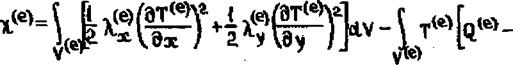 |
где Е - общее число элементов, а вклад каждого элемента в X :
-с rV~Чг(е>Т(е><*Цт4'|г^“гт(е%Т-«+Т“]^ • (3-58)
Здесь верхний индекс (е ) указывает на принадлежность величины данному элементу е. Видно, что свойства элементов по Хх, Ц, ср, вСт могут отличаться, т. е. свариваемое тело может быть разнородным. Далее для удобствалаписи индекс (е) у этих коэффициентов, а танке у Q и q, будем опускать.
Запишем уравнение (3.58) в матричной форме. Для этого введем матрицу
M-ft* У «з.«
х) См., например: Зенкевич С. fife то д конечных элементов в тех-
нике. - Н.: Мир, 1975, с.538-539; или [9], с.376-379.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
 |
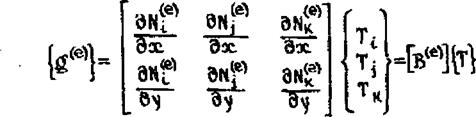
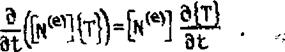
![]()
|
|
|
|
|
|
|
|
|
|
|
|
|
|
![]()
![Метод конечных элементов Подпись: [L‘e’fOTWT}dV-(Q[N®]TdV](/img/3120/image159.gif) 1 * - 4 / ог рь
1 * - 4 / ог рь
+ ^т[мИ]Т[м1е1]{т]лЗ - ^T^Nw]Wo (3.65) . s(e)
![]() так как в соответствии с правилами дафференсртрованяя матричных произведений
так как в соответствии с правилами дафференсртрованяя матричных произведений
![]() здИМ)-&«Ч*к fv<4>
здИМ)-&«Ч*к fv<4>
эд(И>1И)-гМт1 ,
где [М] - матрица или произведение матриц, не зависящих от
М •
Сумму интегралов (3.65) запишем в бодее^ удобной матричной форме
щ-t1'1]^♦[«•'ЧМ'Н • <3-67)
где fe(e,)> cp[Nte^T[N(e)]dV - матрица теплоемкости;
v<e> J
[№]= [в^]тОТ[ь(е^у+ ІЗ -
Vе» f г** г г, „т
матрица теплопроводности элемента; [Sv р Q. lNle’j dV +
у(е)
+ с^[ми]Т45 +■ оіхтДнСбї] dS - вектор тепловой нагрузки. Вычис - лим все эти матрицы ДЛЯ треугольного элемента:
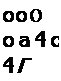
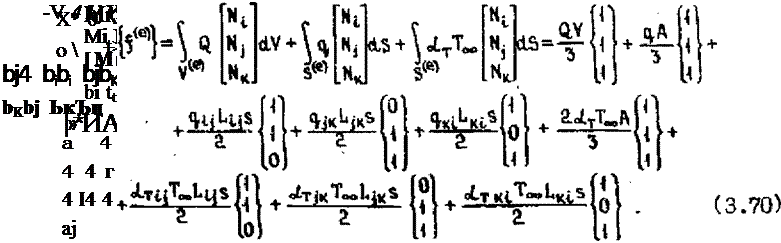 |
ООО
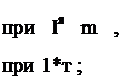 |
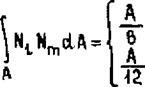 |
Здесь V-As - объем треугольного элемента. Нижние индексы у L 4 , olT указывают стороны треугольника, к которым эти величины относятся; ^ и «1т без индексов относятся к лицевім поверхностям треугольника (2 при «1т сохраняется, если теплоотдача обеих поверхностей одинакова, в противном случае 2ЛТ следует заменить суммой коэффициентов по обеим поверхностям, При выводе формул (3,68)-(3.70) пользовались следующими значениями интегралов (см. 3.5.2 и 8.3 в [9]):
Подставив выражение (3.67) в (3.64), получим окончательную систему дифференциальных уравнений относительно температуры в уаловнх точках всей системы конечных элементов
Чтобы получить значения [Т] во времени, необходимо решить линейное дифференциальное уравнение (3.72). Существуют различные методы решения, мы выберем наиболее простой - метод конечных разностей (см. 3.7.1).
Рассмотрим уравнение (3.72) в средней точке tK_y£ вре-
■ленного интервала ( tKH, tK ) продолжительностью At, Аналогично выражению (3.33) получим
Ш) _{ЛЛт)км Vat /к_£ At ’
Полученное уравнение является основным. Считая температуру 'В узлах в предыдущий момент tKH известной, по этому уравнению можно получить температуру в узлах в текущий момент tK. На первом этапе, , учитываются начальные условия (3.51). При этом в качестве температуры на предыдущем этапе, к-1*0 , принимается температура в узлах [т] согласно закону Т0(х, у) .
До сих пор мы не учитывали одно из граничных условий задачи - условие (3.53). Учтем заданные значения температуры в граничных узлах на этом етапе решения задачи, преобразуя матрицу [к] к вектор (р в уравнении (3.76). Например, если температура в узле с номером п задана Тп=а, то строка п в [к] ,[У) , {?} и столбец п в [к] вычеркиваются, а от каждого элемента Fm столбца свободных членов 1F1 отнимается произведение Kmn*o. (m* I, 2,...), где Kmn - элемент матрицы [к] . После такого преобразования
матрица [к] остается симметричной и ленточного типа. Окончательно сформированная система уравнений (3.76) может быть решена любым известнш методом, например методом Гаусса. Эту
систему необходимо решать на каждом этапе прослеживания по
времени.
Таким образом* мы рассмотрели все этапы решения плоской температурной задачи методом конечных элементов при сварке. Общая блок-схема программы, составленной на основе изложенного алгоритма, показана на рис.3.15. После обилия формул и математических выкладок лучше всего рассмотреть все этапы решения задачи на простом примере, который имитирует условия сварки.
Пример. Пусть сваривается пластина толщиной Юмм Срис. ЗЛб. аЧ Материал пластины однороден, коэффициент теплопроводности Х. х= 0,0^ Вт/мм*°С, объемная тепло
емкость ср = 0,0048 Дж/мм^*°С. Выделим из центральной зоны пластины поперечную полоску площадью 20x10 шг и толщиной I мм (рис.3.16,б'. Пусть в верхней половине полоски, которая имитирует выполняемый односторонний сварной шов и на рисунке заштрихована, действует объемный источник теплоты мощностью Q = 6 Вт/мм3. Будем считать, что передняя и задняя поверхности полосни теплоизолированы ( Хт = 0), на верхней и нижней поверхности происходит теплоотдача в окружапцую среду с коэффициентом в1т= 6*10“^ Вт/мм3-°С, а на боковой поверхности задана температура, которая изменяется по закону (3.9), что имитирует идеальную стыковку выделенной полоски по боковой поверхности с остальной частью пластины. Дополнительные поверхностные источники по всей поверхности отсутствуют ( (^=0). Начальная температура Т0= 0°С. Температура окру - жащей среды Та., = 0°С. Требуется определить температурное поле в полоске через I с после начала действия источника теплоты.
Пронумеруем последовательно все операции согласно нумерации блоков на рис,3.15.
1. В условии задачи сформулированы исходные данные (геометрия тела, свойства материала, режим нагрева, начальные и граничные условия'1.
2, Разбиваем тела по элементам. Так как тело и температурное поле симметричны относительно плоскости х= 0, рассмотрим только правую половину, приняв плоскость х = 0 за адиабатическую границу ( olT= 0). Для простоты расчета разобьем эту половину только на два треугольных элемента с четырьмя узлами, но так, чтобы разность между номерами узлов
|
Рис.3.15. Блок-схема программы, реализующей метод конечных элементов |
элемента была минимальной (рие. ЗЛб. в). Толщина элементов
sw= - I мм, площадь А01 = А(У| = 50 мм2, объем У(<)=
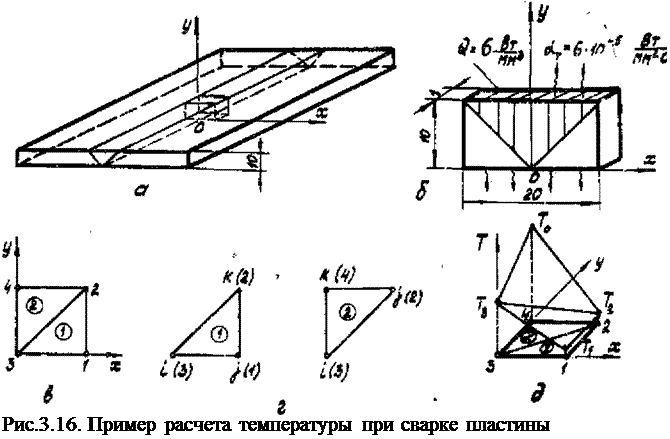 |
- Vй= 50 мм2. Узлы каждого элемента пронумеруем в направлении против часовой стрелки буквами і, і, к, причем первый узел і может быть Выбран произвольно (рис. ЗЛ6,г).
3. Весь заданный период нагрева представим в виде только одного интервала, At = I с.
4. Последовательно для элементов I и 2 вычислим все матрицы.
5. Вычислим матрицу теплоемкости для элемента I по (3.68):
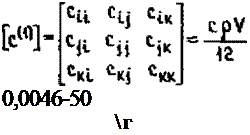 г
г
|
1 і а
|
Здесь систему нумерации узлов i, j,K можно понимать как местную систему.
Матрица теплопроводности [kw] при условии и
‘Нк^ткГО согласно формуле (3,69) равна
Вектор тепловой нагрузки в моменты к-4 = О и к= I для элемента I определим по формуле (3.70):
![]() «V
«V
лов;
![]()
![]()
![]()
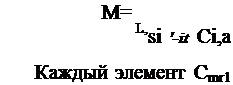 24 ‘•24
24 ‘•24
См Сзд С44 С ц)|
матоицы [С] является суммой соответствующих элементов матриц [Cte1] согласно (3.73). В рассматриваемом случае мы знаем матрицы [сН}] и |Vayj в системе нумерации узлов і, і,к. Включение и [cw1t] в [с] в гло
бальной системе нумерации узлов можно осуществить с помощью соотношений i=3, i=I, к=2 для элемента I и і = 3, 1=2, к.= 4 для элемента 2 (см. рис.3.16,г). Таким образом, получим
|
cJJ+0 |
«8*0 |
0+0 |
|
|
4V" |
«а* |
«8«? |
°+$ |
|
tq+0 |
•sm? |
<2ng |
°+<її |
|
0+0 |
о«5 |
«**8 |
0+cg |

|
о, о*+о |
0,02+0 |
0,02+0 |
0 ' |
0,0*1 |
0,02 |
0,02 |
0 ' |
|
|
0,02+0 |
0,04+ 0,0*1 |
0,02+0,02 0+0,02 |
0,02 |
0,08 |
0,0*1 |
0,02 |
||
|
0,02+0 |
0,02+0,02 0,0*і+0,0*і |
0+0,02 |
0,0? |
0,0*1 |
0,08 |
0,02 |
||
|
0 |
0+0,02 |
0 + 0,02 |
0+0,0*1 |
, 0 |
0,02 |
0,02 |
0,0*1. |
Видно, что матрица [С] симметричная и ленточная, вне ленты шириной 5 диагоналей элементы матрицы равны нулю. Ширина ленты определяется максимальной разностью номеров узлов элемента.
Аналогично включим матрицы и [Vй) в глобальные
матрицы, в результате чего получим
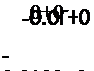 |
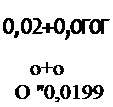 |
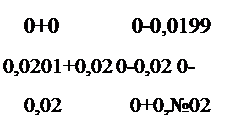 |
Q,0*i02+0 -0,02+0 '0,0199+0 0+0
0, 0Ш -0,02 -0,0199 о
-0,02 0,0^0 г О -0,0199
"0^0199 0 0,0Ш -0,02 ’
0 -0,0199 -0,02 0,0*102
|
F,1 |
'sf+0 } |
о+о V |
г0 1 |
||
|
и>- |
1 |
і to. 3K riS ії’мГ |
1 = 1 |
0+100 І о+шо |
100 100 |
|
и| |
0 |
0+100 р |
100] |
8. С помощью вычисленных матриц [С] , [К] , (р]0 и [F],
по формулам (3.77) окончательно сформируем систему уравнений (3.76):
*
|
'о, одог |
'0,02 - |
0,0199 |
0 |
0,01» |
0,0г |
,Р О Г* о |
||||
|
где [К> |
-о, ой |
o, oiioa |
0 |
■0,0199 |
2 1 |
Ц02 |
QOft |
Qflk • 002 |
||
|
'0,0194 |
0 |
о. ошг |
-0,02 |
+ |
Q02 |
0,01» |
008 0,02 |
|||
|
0 |
-0,0 т |
“0,02 |
0,01*02 |
. 0 |
0,02 |
002 0,04 |
||||
|
о,1 аог |
0,02 |
0,0201 |
0 |
|||||||
|
о, ог |
о, гооа |
0,0ft |
0,0201 |
|||||||
|
0,0201 |
0,02 |
0,2002 |
0,02 |
1 |
||||||
|
. 0 |
0,0201 |
0,02 |
0,1202 1 J |
|
0 |
[01 |
0 ) |
|
|
0 |
^ Г U |
1°о1 |
200 |
|
D |
HQ0 |
100 |
200 |
|
І0 |
[юоі |
.200 |
Заметим, что матрица [к] является симметричной, ленточной и положительно определенной. Положительная определенность означает, что все коэффициенте, стоящие на главной диагонали, положительны. Перечисленные свойства матрицы делах» ее идеальной при использовании вычислительной техники; решение такой системы уравнений существует, и оно единственно.
Э. Приведем систему уравнений (3.80) относительно неизвестных Т4 , t, Т, в развернутом виде:
о, ігогт4 +0,02т., +0,02011^ - о,
Оогт4 + о, гоогт£+о. ов тг + 0,0201^=200,
(3.81)
0,0 гшт4 + о, оатг + о, гоогтэ + 0,02т* = 200, о, огоітг+о, огт3 + o,«ee^=£00.
В действительности по условию задачи температура в узла* I и 2 задана. По уравнению (3.9) она равна 61°С при Q =
= 2x300 Дк и р = 2 мм. Преобразуем систему уравнений с учетом этих граничных условий. Для этого в систему (3.81) подставляем Т4 = 61 и Та — 61, вычеркиваем первое и второе уравнения, исключаем первый я второй столбцы оставшихся уравнений, перенося их в правую часть системы. В итоге получим
преобразованную систему уравнений относительно неизвестных
0,02^+0,1302^=458,8 .
10. Решением преобразованной системы уравнений является
Т%=817 °С, °С .
По известным значениям температуры в узлах можно построить распределение температуры в выделенной ■ полоске
(рис.3.16,д). Исходя из возможности ручного счета, мы очень грубо разбили поперечное сечение на элементы, что, естественно, привело и очень грубш результатам. Для подобного класса температурных задач требуется разбивка на многие десятки и даже сотни конечных элементов, а временной’ интервал fit следует принимать равным долям секунды.
![]() Среди исследователей-сварщиков
Среди исследователей-сварщиков
очень популярны схемы сосредоточенных
источников теплоты. Рассмотрим треугольный элемент толщиной $ с ли - нейным источником теплоты йо/е [Вт/м]
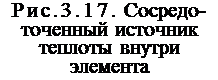
![]()
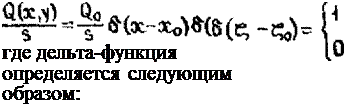 |
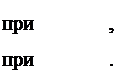 |
в точка х0,у0 (рис.3.17). Распределение такого источника описывается функцией
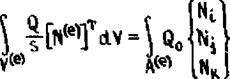 |
Тогда первый интеграл в (3.70)
так как согласно свойству дельта-функции
Остальные члены в уравнениях (3.68'-(3.70) остаются без изменений.
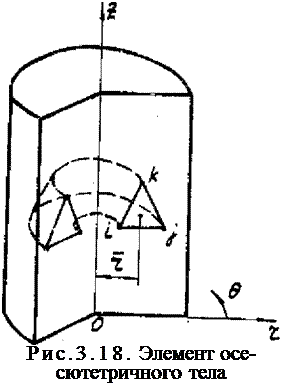 Рассмотрим кратко особенности расчета температурного поля в телах вращения, которые охватив ают большой класс сварных конструкций (трубы, цилиндры, обечайки и т. п.; рис.3,18).Если свойства материала, распределение объемных источников Q, начальные и граничные условия не зависят от азимутального угла 8 , то температурное поле будет осесимметричным и все сечения по оси г подвергнутся одинаковому термическому циклу.
Рассмотрим кратко особенности расчета температурного поля в телах вращения, которые охватив ают большой класс сварных конструкций (трубы, цилиндры, обечайки и т. п.; рис.3,18).Если свойства материала, распределение объемных источников Q, начальные и граничные условия не зависят от азимутального угла 8 , то температурное поле будет осесимметричным и все сечения по оси г подвергнутся одинаковому термическому циклу.
Расчет осесимметричного
температурного поля можно свести к уже рассмотренной плоской задаче, если под х понимать г, под v-^ > а толщину элемента принять переменной и зависящей от радиуса г , s=2.$rr. При этом интегрирование в формулах (3,68)-(3.70) при вычислении матриц [е(е13 , и (3(е^ усложняется, поскольку
толщина а не выносится за знак интеграла. Если площадь элементов достаточна мала, то можно считать толщину элемента постоянной и равной его толщине в центре элемента с координатой г= (гч + г^+ГкУЭ. При таком приближенном подходе вид
формул (3.68)-(3.70) сохраняется, если под толщиной s понимать величину 2jrr.


 Опубликовано в
Опубликовано в