В простой передаче I равно отношению радиусов, а в волновой — отношению радиуса ведомого колеса к разности радиусов или к раз­меру деформирования W0.

Очевидно, что разность радиусов можно выполнить малой, a I — большим. Большое I — одно из положительных качеств вол­новой передачи. Величина w для фрикционных передач ограничи­вается точностью изготовления или допускаемыми отклонениями размеров диаметров. Практически выполняют w«1000. Величину 4iin ограничивает прочность гибких колес, так как напряжения в них пропорциональны размеру деформирования w0. При стальных гиб­ких колесах imin«80. Ограничение — один из недостатков волно­вых передач.

По структуре волновая передача, подобно планетарной, являет­ся трехзвенным механизмом. Она может работать не только как редуктор или мультипликатор, но и как дифференциал.

Метод Виллиса позволяет просто получить формулы для пе­редаточных отношений, но не вскрывает принципа преобразования параметров движения путем деформирования гибкого звена ме­ханизма.

/Действительно, в передачах с жесткими звеньями, например в простой фрикционной передаче, при вращении одного колеса точки его поверхности получают окружную скорость, и если к этому колесу прижать другое, то оно получит ту же окружную скорость, а угловые скорости колес будут обратно пропорциональны их ради­усам.

Как же образуются окружные скорости в волновой передаче? Как вращение генератора передается жесткому колесу через не - вращающееся гибкое колесо?

Для того чтобы выяснить это, рассмотрим движение точек не - вращающегося гибкого колеса при его деформировании вращаю­щимся генератором. Отметим, что в нашей конструкции гибкое колесо подобно оболочке (толщина значительно меньше других размеров).

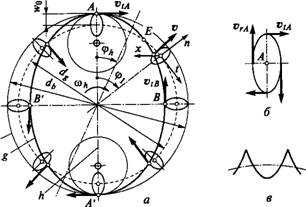
В теории оболочек обычно рассматривают перемещения точек срединной поверхности (поверхность посредине толщины оболочки) в координатах х, п, T (рис. 10.3). Начало координат совмещают с положением рассматриваемой точки до деформирования. Ком­поненты перемещений обозначают: W — радиальные, V — окру­жные, и — осевые.

Перемещение и не оказывает влияния на кинематику передачи. Поэтому рассмотрим плоскую задачу, в которой учитываем только W и V на краю цилиндра. Кроме того, в первом приближении не учитываем влияние толщины оболочки.

Полагая, что генератор обеспечивает деформирование края ци­линдра по форме, для которой 232

И> = ф! (фО,

Где (р — угловая координата точки на срединной поверхности до деформирования, отсчитываемая от большой оси генератора.

По условиям конструкции функция Ф(ф) должна быть пери­одической (период я) с максимумами в точках А и А и минимумами в точках В и В. При этом независимо от формы деформирования у фрикционных передач

(10.4)

A wmь изменяется в зависимости от формы.

По условию прочности W0 В волновых передачах обычно не превышает толщины цилиндра. При этом для определения окру­жных перемещений V используют условие нерастяжимости из те­ории оболочек (периметр цилиндра при деформировании не изменя­ется)

Dv/D<р= —W или V— —$ц>д.(р = Ф2(Cpi).

В дальнейшем условимся решения, записанные в общем виде, иллюстрировать простейшим примером, в котором примем форму деформирования по закону w=w0cos2<pi.

При этом по формуле (10.5) «= — 0,5H>0sin2<pi.

Окружное перемещение имеет максимум при (рх=45° и в два раза меньше wmax=w0. В той же точке и>=0.

Функции (10.3) и (10.5) выражают статическую форму гибкого колеса. При вращении генератора с угловой скоростью coh текущее положение рассматриваемой точки относительно его большой оси
в момент времени T определяется углом (P = (Pl — (Ph=(Pl — Coht. При этом формулы (10.3) и (10.5) можно записать в виде

W=<E>I(q>i — coht), « = Ф2(<Pi-coht). (10.6)

Пример, W=Wqcos2(<рх — corf), V=— 0,5н>0sin2(<j— A>HT).

Уравнения (10.6) определяют траекторию движения точки, рас­положенной под углом ф]а Здесь Q>{= const — начальный угол, а движение вызвано вращением генератора. Траектория выражается некоторой замкнутой кривой; на рис. 10.3, а она изображена тонкой линией, на рис. 10.3, б — с увеличением. При вращающемся гибком колесе замкнутая овальная траектория принимает форму, изобра­женную на рис. 10.3, в.

За один оборот генератора любая точка невращающегося гиб­кого колеса совершает два пробега по своей траектории. Траек­тории всех точек гибкого колеса одинаковы. Движение по ним отличается только сдвигом фазы (фазовым углом q>i).

Дифференцируя функции (10.6) по времени, получаем компонен­ты скорости движения точек: радиальная скорость

Vr=Dw/Dt=(D/Dt)0{ (<Pi - шЛ/); (10.7)

Окружная скорость

Vt=Dvjdt=(D/Dt) Ф2 (<р — Coht). Используя условие (10.5), записываем

Vt= — (d/dt) J Ф I (<Pi - coht) dep. В нашем случае dq>= —cohdt. При этом

Vt=(Ј>h<&(<P- coht)=Cohw. (10.8)

Пример. vr=Сон 2Wq sin2(<pi — VT=^иЩ cos 2 (<P — Corf).

Окружная скорость точки равна произведению ее радиального перемещения на угловую скорость генератора.

В соответствии с принятыми условиями для точек А и В, со­впадающих с большой и малой осями генератора, wA = wQ и wB= = — KwQ, где К — постоянная, зависящая от формы деформирова­ния (для примера К= 1). При этом

VrA=vrB=dw/dt=0; (10.9)

VtA = wQcoh, vtB= -Kw0coh; (10.10)

VtA не зависит от формы деформирования и направлена в сторону вращения генератора; VtB зависит от формы деформирования и на­правлена против вращения генератора.

Точки А и В движутся в противоположных направлениях. В про­межутке АВ существует некоторая точка Е, для которой VtE=0, A VrE имеет максимум. Положение точки Е зависит от формы деформирования (обычно близко к 45°).

В примере точка Е расположена под углом 45°, ее скорость

VrE=2w0(oh, А vtE=0.

Для фрикционной передачи имеют значение только скорости в точках А и А'. Они равны. Скорость VtA гибкого колеса одновре­менно является и окружной скоростью жесткого колеса (без учета проскальзывания).

Точка контакта гибкого и жесткого колес перемещается вместе с генератором и остается в вершине бегущей волны деформирова­ния. При этом окружная скорость ведомого звена (жесткого или гибкого колеса) остается постоянной: VtA = W0Coh = const. Постоянным будет и передаточное отношение. В этом проявляется весьма остро­умное использование принципа деформирования для преобразова­ния движения в волновых передачах.

На основе анализа скоростей можно получить зависимость для передаточных отношений. Угловая скорость колеса Ь

А>ь=2VU/Db = coh 2w0/Db.

Передаточное отношение от генератора А к колесу Ь при непо­движном колесе G

Чь = ojh/ojb=db/(2w0) = db!(db - dg).

При неподвижном колесе Ь колесо G вращается навстречу гене­ратору. Относительная скорость вращения генератора ^ и колеса G Cohg=Coh--(Og. При этом окружная скорость в точке A VtA = WQ(Coh + + угловая скорость

Щ=2 vtAl(dg+2и>0)=2wq (i(oh + |ю,| )/(dg+2и>0),

Где (Dg+2W0)/2— радиус-вектор деформированного колеса в точ­ке А.

После преобразования с учетом знака Cog получим 4 = (Dh/(Dg = - Dg/(2W0) = - Dg/(Db - Dg).

Как и следовало ожидать, получены прежние зависимости (10.2), но не по методу Виллиса, а по методу скоростей волнового дефор­мирования. В дальнейшем этот метод позволит учесть еще и дру­
гие особенности кинематики волновых передач (см., например, § Ю.4).

Сопоставляя структурные схемы волновой передачи и ранее известных передач, можно отметить следующие принципиальные различия; все ранее известные механические передачи являются механизмами с жесткими звеньями; волновая передача содержит гибкое звено; во всех передачах с жесткими звеньями преобразова­ние движения осуществляется или по принципу рычага, или по принципу наклонной плоскости. Принцип рычага используют в из­вестных зубчатых, фрикционных, ременных и цепных передачах, где отношение радиусов колес функционально подобно отношению плеч рычага. По принципу наклонной плоскости работают червяч­ные и винтовые передачи.

В волновой передаче преобразование движения осуществляется путем деформирования гибкого звена. Этот принцип назовем прин­ципом деформирования. Сущность этого принципа в том, что при волновом деформировании гибкого колеса всем его точкам сообща­ются окружные скорости. При контакте гибкого колеса с жестким по вершинам волн окружные скорости волновых перемещений сооб­щаются жесткому колесу (или гибкому), как ведомому звену пере­даточного механизма.