В приведенном выше примере мы использовали нормальное рас­пределение, однако если есть реальные данные, то для калибров­ки рекомендуется брать их. Предположим, мы хотим спрогнози­ровать валовую прибыль продаж продуктов 1 и 2, используя про­стую финансовую модель (табл. 7.19).

У нас есть исторические данные о продажах этих продуктов в течение 360 предыдущих периодов (рис. 7.18).

Рисунок 7.18

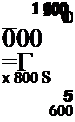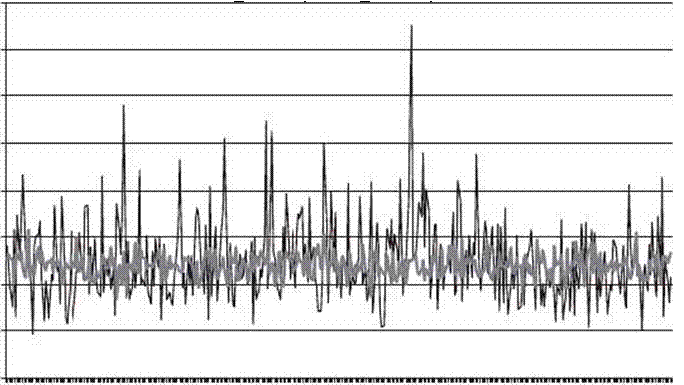Исторические данные о продажах продуктов 1 и 2

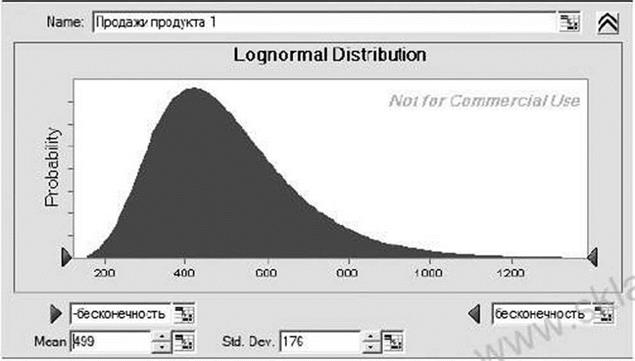
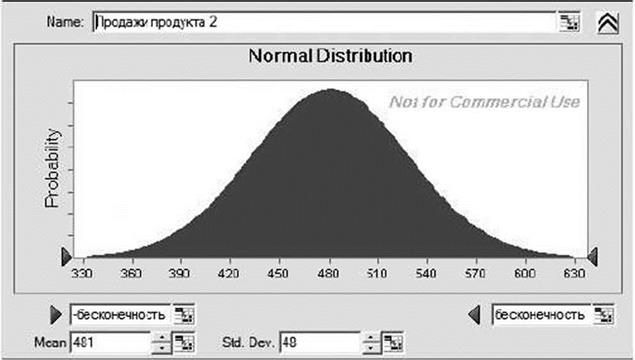
Мы можем подобрать распределение, которое статистически наиболее точно подходит для моделирования продаж. В данном случае продажи продукта 1 наиболее точно моделируются логнор­мальным распределением с ожиданием 499 и стандартным от­клонением 176 (рис. 7.19). Для продаж продукта 2 лучше всего подходит нормальное распределение с ожиданием 481 и стан­дартным отклонением 48 (рис. 7.20).

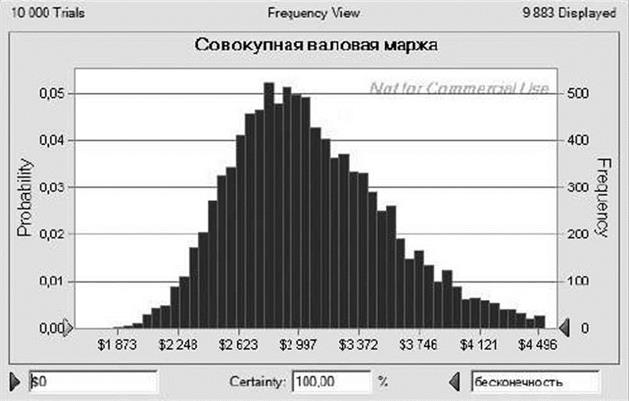
Используя подобранные распределения, получаем прогноз со­вокупной валовой маржи продаж двух продуктов (рис. 7.21).