В настоящее время для прогнозирования процесса разрушения конст­рукций при циклическом нагружении используются аналитические модели, разработанные для анализа относительно простых тел с трещинами. Нали­чие мощного математического аппарата механики трещин и относительная быстрота и легкость получения информации способствовали широкому рас­пространению этих моделей и переносу основных идей аналитического мо­делирования на случаи анализа долговечности и надежности сварных кон­струкций. Когда закономерности процесса разрушения сварных соединений сложны и многообразны, зачастую приходится идти на упрощения реальных явлений. В результате этого аналитическая модель может стать слишком грубым приближением к реальной действительности.

Имитационное моделирование значительно расширяет возможности учета отдельных особенностей процесса развития разрушения сварных со­единений, особенно для крупногабаритных конструкций, когда конструк-

тивных концентраторов напряжений и очагов разрушения может быть не­сколько.

Имитация представляет собой численный метод проведения компью­терных экспериментов с математическими моделями, описывающими пове­дение конструкции при заданных параметрах нагружения в течение заданного или формируемого в ходе имитационного эксперимента периода времени.

В имитационной модели процесс разрушения описывается набором алгоритмов, которые затем реализуют ситуации, возникающие в реальной сварной конструкции. Моделирующие алгоритмы позволяют по исходным данным, содержащим сведения о начальном состоянии сварного соедине­ния, и фактическим значениям параметров сопротивления разрушению ото­бразить реальный механизм зарождения и роста трещин в конструкции, а также получить сведения о возможных вариантах кинетики разрушения в данной конкретной ситуации.

Возможность описания процесса разрушения сварных соединений на высоком уровне детализации, отсутствие ограничений на виды используе­мых аналитических моделей и конструктивно-технологические параметры исследуемого объекта, возможность исследования кинетики взаимодействия отдельных очагов разрушения во времени и пространстве выдвигают ими­тационное моделирование в число перспективных методов компьютерного прогнозирования разрушения конструкций.

Имитационное моделирование можно рекомендовать для исследова­ния процесса разрушения сложных объектов в случаях, когда

• аналитические методы имеются, но математические процедуры столь сложны и трудоемки, что имитационное моделирование дает более простой способ решения задачи;

• кроме оценки влияния конструктивно-технологических параметров сварной конструкции на конечные результаты моделирования желательно осуществить наблюдение за протеканием накопления повреждений и кине­тикой развития разрушения в исследуемом объекте в течение определенного периода;

• не существует законченной постановки задачи исследования и идет процесс анализа объекта моделирования; имитационная модель может слу­жить средством изучения явления;

• формирование процесса разрушения определяют несколько незави­симых механизмов и особое значение имеет последовательность событий их включения.

Во многих случаях имитационное моделирование оказывается един­ственным способом исследования кинетики разрушения сложной сварной конструкции, поскольку оно позволяет в зависимости от сложившейся си­туации в ходе имитационного эксперимента изменять набор используемых аналитических моделей и/или параметров и характеристик дальнейшего протекания процесса разрушения.

Алгоритмической основой для имитационного моделирования разру­шения являются принципы событийности, дискретизации времени и слу­чайности перехода модели из одного состояния в другое. Принцип собы­тийности дает возможность процесс разрушения условно разделить на ряд характерных состояний модели. Дискретизация времени позволяет объеди­нить во времени и описать в рамках единого алгоритма процессы, проте­кающие при различных состояниях модели, например зарождение разруше­ния, развитие трещины, переход к нестабильному разрушению.

Чтобы обеспечить имитацию параллельных событий, протекающих при одном зафиксированном состоянии модели, вводят некоторую глобаль­ную переменную to, которую называют модельным временем. С помощью этой переменной организуется синхронизация всех событий в модели и вы­полнение алгоритмов.

Корректировка временных координат нескольких параллельно проте­кающих процессов осуществляется с помощью модельного времени сле­дующим образом. Если в реальной системе происходит одновременно не­сколько событий, то имитационная модель последовательно обслуживает все алгоритмы, имитирующие процессы, совпадающие по времени выпол­нения, при этом модельное время не меняется до окончания выполнения всех совпавших по времени реализации алгоритмов. Таким способом после­довательное выполнение соответствующих действий, но при неизменном значении to, имитирует параллельность протекания процессов.

Построение имитационной модели начинают с вербального описания закономерностей процесса разрушения, на основании чего разрабатывают алгоритм модели, определяют необходимый перечень аналитических моде­лей, критерии и условия их включения в имитационную модель в ходе ма­шинного эксперимента, задают исходные данные, характеризующие меха­нические свойства, в том числе сопротивление разрушению.

Исходные данные по своей природе могут быть как детерминистиче­скими, так и стохастическими. В последнем случае необходимо задать соот­ветствующие законы распределения случайных величин и их параметры. Необходимо установить пределы изменения значений переменных или оп­ределить условия, ограничивающие их изменения. Они могут вводиться ли­бо в виде исходных данных при разработке модели, либо в виде алгоритма, устанавливающего их в ходе машинного эксперимента в зависимости от со­стояния имитационной модели. Также должны быть установлены цели и задачи моделирования, необходимые правила и критерии оценки их выполнения.

Рассмотрим применение метода имитационного моделирования на примере создания модели зарождения и развития разрушения в сварных конструкциях при циклическом нагружении.

В сварных соединениях с механически необработанными швами уста­лостное разрушение инициируется, как правило, в зонах концентрации на­пряжений около линии сплавления, образуя так называемый линейный ини­циатор. Характерной особенностью таких инициаторов является взаимное влияние соседних очагов разрушения. Развитие разрушения в данном случае может быть представлено в виде случайного сочетания нескольких одно­временно развивающихся процессов: зарождение отдельных трещин на раз­личных, не связанных между собой участках-инициаторах; их рост и появ­ление новых трещин; объединение между собой трещин, развивающихся на соседних участках. Такой характер разрушения назван многоочаговым раз­рушением.

Стохастическая природа явления создает предпосылки к многовари­антности путей и траекторий развития разрушения. Имитационная модель предполагает последовательную пошаговую имитацию реального характера распространения разрушения в конструкции с учетом вероятностной приро­ды действующих факторов. Имитационное моделирование позволяет на ка­ждом шаге оценивать сложившуюся ситуацию и в соответствии с ней опре­делять дальнейший ход развития разрушения, учитывать влияние неизбежно присутствующих случайных возмущений процесса. В частности, можно учитывать акты появления новых очагов разрушения и связанное с ними изменение НДС конструкции, объединение соседних трещин, возникнове­ние на отдельных участках актов хрупкого разрушения или коррозионного растрескивания и т. д. Все это позволяет учитывать в машинном экспери­менте многовариантность путей эволюции разрушения в сложных сварных конструкциях, приближая тем самым его к реальности.

Сценарий имитационного моделирования многоочагового разрушения при линейном инициаторе состоит в следующем:

• в пределах одного сварного соединения наибольшее относитель­ное колебание имеют радиус г перехода от шва к основному металлу и угол 0 сопряжения. Именно эти два параметра оказывают главное влия­ние на значение и характер изменения концентрации напряжений вдоль кромки шва;

• линия перехода от шва к основному металлу представлена в виде дискретного набора из і участков, длина /, которых изменяется случайным образом. В пределах каждого участка очертания профиля перехода от шва к основному металлу принимаются неизменными, а значение коэффициента концентрации деформаций Кеі, зависящее от типа соединения и локальных параметров г и 0, постоянным (Kei = const). Интегральная функция распреде­ления F{1,) определяется экспериментально на лабораторных образцах кон­кретного типа соединения и технологии изготовления. Экспериментально установлено, что для сварных соединений с механически необработанными
после сварки швами распределение случайной величины /,- подчиняется за­кону Вейбулла—Г неденко

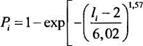(3.26)

Параметры распределения значений г и 0 зависят от типа соединения, способа сварки, сварочных материалов и других факторов (см. табл. 3.7);

• длительность периода до зарождения трещины N3i на каждом участ­ке рассматривается как случайная величина, зависящая от коэффициента концентрации деформаций Kei, амплитуды номинальных деформаций еном и свойств материала. Период N3i рассчитывается по уравнению малоцикловой усталости в предположении, что Kei является случайной величиной, завися­щей от функций распределения F(r) и F(0) или генерируется компьютером в соответствии с интегральным законом распределения F(N3), подлежащим экспериментальному определению. Принимается, что на г-м участке возни­кает трещина длиной /, и глубиной 6,= 0,5 мм при достижении N = jV3;

• случайные величины /, и Kei являются независимыми;

• рост поверхностных трещин подчиняется законам механики разру­шения с учетом случайной вариации параметров кинетической диаграммы разрушения;

• в процессе подрастания трещин на отдельных участках их взаимное влияние на скорость распространения разрушения не учитывается вплоть до объединения соседних трещин. Объединение соседних трещин производит­ся при выполнении условия

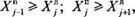(3.27)

где X"; X* — координаты правой и левой вершин поверхностной трещины

на /-м участке в системе координат, для которой нулевая точка совмещена с началом шва. Размер трещины вдоль малой полуоси 6, принимается равным наибольшему из значений для трещин, подлежащих объединению;

• в качестве модельного времени используют значение числа циклов N, изменяют N с шагом AN и подсчитывают характеристики нового состоя­ния модели;

• после моделирования каждого шага AN анализируют сложившую­ся ситуацию с развитием разрушения и вводят корректировку в дальней­ший ход имитационного моделирования. Например, если фронт несквоз­ной трещины выходит на поверхность сварного соединения, то изменяют
аналитические модели, используемые для расчета подрастания трещины; если выполняется условие слияния соседних трещин (см. § 3.3), то про­изводят их слияние и соответственно изменяют параметры формы фронта трещины;

• анализируют достижение процессом заданного предельного состоя­ния и решают вопрос о целесообразности продолжения моделирования.

Для расчета длительности периода зарождения усталостной трещины может быть использован подход, предложенный в § 3.3. Для моделирования роста трещины, как правило, используют кинетическую диаграмму устало­стного разрушения (3.3). В зависимости от ситуации, складывающейся в ка­ждый период модельного времени, управляющая программа с помощью банка теоретических зависимостей формирует математическую модель и включает ее в алгоритм имитационного моделирования.

Для эффективной работы имитационной модели необходимо иметь банк исходной информации, содержащий статистически представительный объем экспериментальных данных следующего вида:

• тип и параметры распределений, характеризующих геометрические размеры дефектов. Сюда относятся данные о геометрии профиля перехода от шва к основному металлу для различных технологических вариантов сварки, данные о размерах и частоте появления внутренних дефектов (пор, трещин, шлаковых включений) и т. д.;

• характеристики сопротивления различных участков сварного соеди­нения зарождению разрушения, характеристики трещиностойкости сварного соединения при циклическом и статическом нагружении на воздухе и в кор­розионной среде.

Имитация должна предусматривать случайность и многовариантность развития процесса разрушения. С этой целью имитационная модель задает с помощью генератора случайных чисел координаты расположения, размеры и вид исходного дефекта, параметры, характеризующие свойства металла, сопротивление зарождению и росту трещины. При наличии достаточных ресурсов компьютера в процессе машинного эксперимента может также из­меняться случайным образом амплитуда внешней нагрузки и учитываться эффект закрытия трещины.

Исходные данные для параметров, характеризующих процесс, должны быть получены на основании статистического анализа результатов эксперимен­тов и представлены в виде соответствующих законов распределения случайных величин. Могут быть использованы данные, приведенные в разд. 3.4.1.

Имитационную модель воспроизводят на компьютере десятки и сотни раз при различных исходных состояниях генератора случайных чисел (ГСЧ) и статистически обрабатывают результаты моделирования.

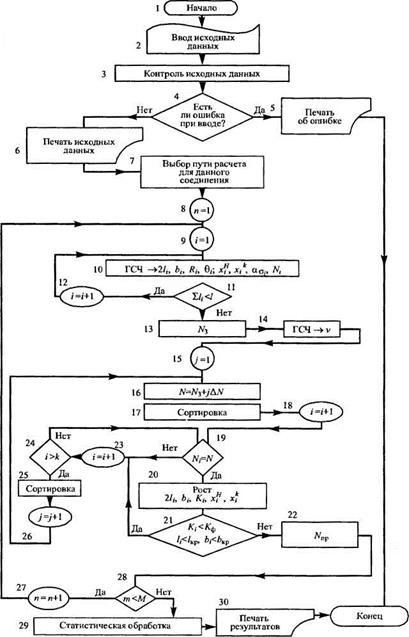
Рис. 3.34. Укрупненная структурная схема алгоритма имитационного моделирования процесса разрушения сварных соединений, работаю­щих при циклическом нагружении

На рис. 3.34 показана укрупненная структурная схема алгоритма ими­тационного моделирования процесса разрушения сварных соединений, ини­циируемого от границы перехода «шов — основной металл». Блоки 1—6 осуществляют ввод и контроль исходных данных, содержащих сведения о типе соединения, схеме нагружения, уровне нагрузки, используемых мате­риалах и т. д. В блоке 7 в зависимости от вида входной информации форми­руется математическая модель расчета, в которой учитываются тип сварного соединения, характер напряженного состояния и вид нагружения, возмож­ность появления внешних возмущающих воздействий и т. д. Блоки 8, 9 при­водят в исходное состояние счетчики циклов по количеству п прогонов мо­дели и числу і участков с однородной геометрией вдоль границ шва.

В блоках 10—12 с помощью генератора случайных чисел и данных о параметрах распределений, получаемых из информационного банка в зави­симости от вида исходной информации, анализируется распределение гео­метрической неоднородности вдоль зоны сплавления сварного шва и фор­мируются выборки случайных значений долговечности до зарождения тре­щин А3 на различных участках шва, длины появляющихся трещин и их глубины Ь,. В блоке 13 из массива {Ж,} определяется минимальное значение Жзтіт соответствующее длительности периода до зарождения первой тре­щины. В блоке 14 с помощью датчика случайных чисел выбирается значе­ние параметров функции (3.3), а в блоке 15 приводится в исходное состоя­ние счетчик циклов, определяющий количество приращений нагружения ДА.

В блоках 16—20 реализуется моделирование процесса развития раз­рушения. Этот этап моделирования является наиболее важным и сложным для алгоритмизации, так как связывает неразрывно во времени, с учетом стохастических закономерностей усталостного разрушения, две стадии, от­личающиеся механизмами разрушения, — стадию зарождения трещин и стадию их развития.

Алгоритм имитационной модели в данном случае организован сле­дующим образом. В блоке 16 задается приращение числа циклов нагруже­ния на ANj и анализируется текущее состояние накопленного уровня повре­ждений с точки зрения размеров трещин и их расположения. Затем сорти­руются массивы {Ж3}, {/,}, {hi} и выбираются такие трещины, для которых значение А3, удовлетворяет условию А3, < А + ANj. Для периода ANj подсчи­тывается подрастание трещин в длину Д/, и глубину АЬ: и анализируется возможность объединения двух и более трещин, расположенных рядом (блок 20). В течение периода ДА,- в реальных условиях работы конструкции одновременно протекает ряд разнообразных процессов, обслуживаемых имитационной моделью последовательно, но благодаря введенному поня­тию «машинное время», которое остается неизменным на протяжении ДА) и изменяется скачком по его истечении, в модели происходит имитация па­раллельно протекающих процессов. В связи с этим на выбор значения ANj следует обратить особое внимание, поскольку его уменьшение ведет к росту машинного времени счета, а увеличение — к снижению точности модели­рования реальной ситуации.

В блоке 21 рассматривается возможность достижения предельного со­стояния разрушения по условиям Кі> Кїс, bimах> Ькр, /,тах> /кр, и если одно из них выполняется, то значения N3m[n, предельной долговечности Np = +

+ lANj, bmm и Zmax помещаются в банк результатов, а управление передается в блок 9 на начало нового прогона модели. В ином случае изменяется со­стояние счетчика циклов и управление передается в блок 16, осуществляю­щий следующий шаг по приращению числа циклов нагружения на ANj.

Количество прогонов модели регистрируется в блоке 27. Опыт пока­зывает, что в зависимости от рассеяния параметров, характеризующих слу­чайный процесс развития разрушения, заданное число прогонов модели мо­жет составлять 500...1000. После завершения работы массивы результатов счета подвергаются статистической обработке в анализаторе 29 с целью оп­ределения средних значений N3, Np, Zmax, femax, их дисперсий и доверительных интервалов, а также оценки у-процентного ресурса.

Многократная прогонка модели на компьютере при измененных со­стояниях датчиков случайных чисел и последующая статистическая обра­ботка результатов численного эксперимента позволяют учесть влияние слу­чайного рассеяния параметров, характеризующих долговечность до зарож­дения разрушения и трегциностойкость, а также случайный характер топографии очагов разрушения и траектории роста трещин.

Рассмотрим возможности предлагаемой методики на примере анализа кинетики разрушения и прогнозирования долговечности сварных штуцер­ных соединений оболочковых конструкций, работающих в условиях двух­осного поля напряжений с компонентами Oi/a2 = 0, 0,5 и 1,0. В расчетах бы­ли приняты следующие исходные данные: материал — хромоникельмолиб - деновая сталь толщиной 30 мм (оог = 1020 МПа, аь= 1150 МПа, у = 0,58); геометрия соединения — диаметр штуцера 90 мм, катет шва, прилегающий к стенке штуцера, — 15 мм, к стенке корпуса обечайки — 30 мм; функция распределения коэффициентов концентрации напряжений соответствует случаю ручной дуговой сварки аустенитными электродами; характер нагру­жения повторно-статический, цикл пульсирующий, номинальные напряже­ния оН0М = 550 МПа. Количество прогонов модели — 500.

Имитационное моделирование выявило специфику кинетики разру­шения, заключающуюся в том, что изменение соотношения компонент на­пряжений (т — o2/oi) сопровождается изменением топографии разрушения. При с2 = о, трещины зарождаются вдоль кромки шва с одинаковой интен-

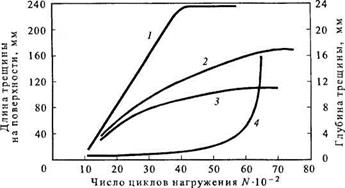
Рис. 3.35. Влияние соотношения компонент двухосного растяжения на рост поверх­ностной трещины по границе кругового шва, соединяющего щтуцер с оболочкой:

1, 4 — т = 1; 2 — т = 0,5; 3 — т == 0; 1—3 — длина трешины по дуге поверхности; 4 — раз­мер трешины по глубине

сивностью по всей окружности. Объединение отдельных трещин приводит к образованию на некотором участке поверхностной дугообразной трещины, длина которой интенсивно растет с увеличением числа циклов нагружения (рис. 3.35, кривая 1). В результате этого на относительно ранних этапах на­гружения образуется сплошная круговая трещина, которая в дальнейшем растет в глубину.

При неравноосном нагружении поверхностная трещина охватывает лишь часть окружности и интенсивность изменения ее длины значительно меньше (рис. 3.35, кривые 2, 3). При определенном соотношении парамет­ров трещины Ы1 возникают условия для изменения траектории разрушения в направлении от границы шва. Например, при глубине трещины Ъ = 5,5 мм угол охвата штуцера трещиной составляет 122° при о2 = 0,5ai и 84° при a2/oi = 0. Изменение схемы напряженного состояния от о2 = 0,5сц до сц = о2 приводит к уменьшению параметра N3 почти в 3 раза.

Имитационное моделирование позволяет проанализировать влияние конструктивных параметров и схемы напряженного состояния на живучесть сварного соединения. Анализ расчетных данных свидетельствует о том, что увеличение диаметра шва штуцерного соединения от 150 до 350 мм (за диа­метр шва принята сумма диаметра штуцера и удвоенного значения катета шва) при неравноосной схеме (ст2 = 0,5а0 незначительно влияет на живу­честь конструкции с трещиной Nc. В то время как при равноосной схеме напряженного состояния такое же изменение диаметра приводит к умень­шению у-процентного значения параметра Nc почти в 2 раза, а среднего зна­чения — в 1,5 раза.

Закономерности развития разрушения в большинстве случаев не под­даются умозрительному анализу. В связи с этим метод имитационного мо­делирования целесообразно использовать на этапе проектирования для оп­тимизации конструктивно-технологических решений с целью согласования заданного и достижимого ресурсов сварных соединений.

Пошаговый принцип анализа развития разрушения обеспечивает гиб­кое реагирование алгоритма модели на любые случайные возмущения и по­зволяет, в зависимости от сложившейся ситуации, адаптировать его к изме­нившемуся механизму. При этом важным является то обстоятельство, что система имитационного моделирования функционирует как открытая и мо­жет уточняться и дополняться по мере поступления сведений, отражающих новые аспекты поведения объекта в процессе его эксплуатации.