Особое значение в процессе получения заготовок и изготовления деталей имеют вопросы экономии материала. Она может быть обеспечена путем замены полос, нарезаемых из листа, лентами, нарезаемыми из рулона. Потери металла при изготовлении деталей из полос образуются в связи с тем, что каждая первая или последняя деталь идет в брак из-за несовпадения края полосы с контуром детали в штампе. Кроме того и наличие шаговых ножей также увеличивает расход материала. Экономия металла может быть достигнута в результате применения автоматических комплексов, где обеспечивается кратность шага и реализуется возможность использования длинных полос, вместо коротких.

Изготовление деталей из рулонного материала без его разрезки на узкие ленты позволяет увеличить число рядов штамповки и реализовать наиболее оптимальный раскрой материала. Основные принципы такого раскроя основаны на механической аналогии, представляющей размещение фигур, как твердых плоских тел, соприкасающихся без трения. При этом рассматриваются силы давления, приложенные к телам в точках, их взаимного контакта и направленные по нормали к поверхности в этих точках. В случае равновесия системы тел под действием указанных сил площадь, занимаемая этими телами, достигает минимума. Силы давления сторон прямоугольника на охватываемую фигуру (рис.8.6)

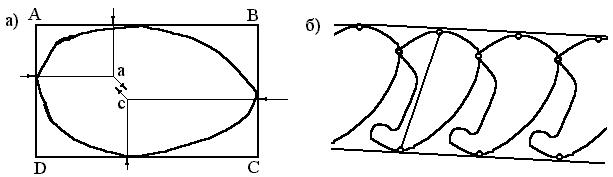
Рис. 8.6 Схема сил давления.

Принимаются численно равными длине соответствующих сторон. Сложением сил, действующих на стороны и , и соответственно, находят их равнодействующие. Полученные две силы должны быть равны и противоположно направлены. Для равновесия необходимо и достаточно, чтобы они лежали на одной прямой. Если это условие не выполняется, то отличный от нуля момент этих сил показывает направление, в котором следует повернуть фигуру, чтобы уменьшить площадь прямоугольника, сохраняя направление его сторон.

При однорядной штамповке из ленты в начале находят минимальную площадь прямоугольника, охватывающего фигуру, а затем совмещают две равные стороны этих прямоугольников. Другим необходимым условием, при котором достигается наиболее плотное заполнение площади ленты, является параллельность линий, проходящей через точки касания фигуры с краями ленты и касательной в точке соприкосновения фигур (рис.8.7).

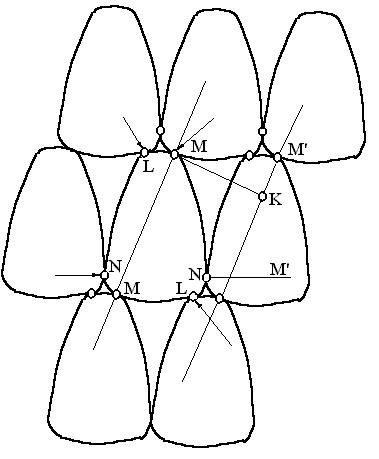
Рис. 8.7 Заполнение плоскости параллельно расположенными одинаковыми фигурами.

Заполнение плоскости рядами параллельно расположенных одинаковых фигур производится по этому же принципу равновесия твердого тела под действием внешних сил (рис.8.6). При этом сила в точке выбирается пропорционально расстоянию

.

На стадии технологической подготовки производства наиболее удобен графоаналитический способ плотного размещения фигур, разработанный Г. А. Навроцким, В. К. Сенько и Ф. Ф. Буйволовой. В его основу заложен метод годографа функции плотного размещения. Плотное размещение заготовок графоаналитическим способом производится в три этапа. Первый этап включает выбор полюса деталей, построения эквидистанты, построения годографа функции плотного размещения, определения вариантов плотного размещения. Второй этап – это построение выпуклого многоугольника, описывающего эквидистанту, определение вариантов плотного размещения по выпуклому многоугольнику. Третий – выбор наивыгоднейшего варианта плотного размещения деталей.

По чертежу выбирается полюс детали (рис.8.8),

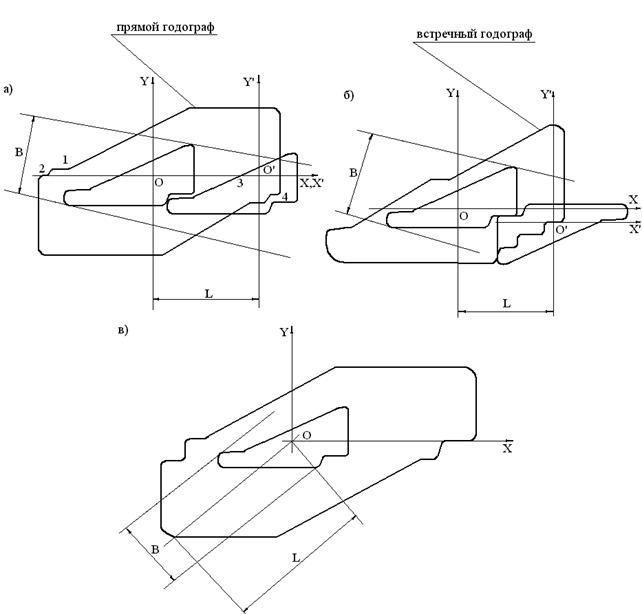
Рис. 8.8 Построение годографов.

представляющий точку пересечения осей симметрии детали (если такие имеются ) или осей симметрии отдельных геометрических фигур, из которых построена деталь. Через полюс проводят оси координат, а саму деталь располагают таким образом, чтобы одна из ее сторон была параллельна оси . Размеры детали увеличиваются на половину междетальной перемычки, в результате чего вокруг детали строится эквидистантная линия. Во всех дальнейших построениях под деталью понимают фигуру, размеры которой увеличены на половину перемычки.

Для построения годографа изготавливают копию детали с обозначенным полюсом и осями координат. Годографом будет являться линия, описываемая полюсом при перемещении одного чертежа детали по другому, остающемуся неподвижным. Перемещение производится таким образом, чтобы детали не накладывались друг на друга, а только касались. При этом необходимо соблюдать параллельный перенос осей координат. В результате такого построения получается прямой симметричный годограф (рис.8.8а). При построении схемы раскроя с поворотом одной детали относительно другой на получается встречный годограф (рис.8.8б). Для определения вариантов размещения деталей на материале используется свойство годографа, заключающееся в том, что функция плотного размещения имеет наименьшее значение во впадинах годографа (точки 1 – 4). Эти точки называются критическими. Одну из них соединяют с полюсом неподвижной детали и параллельно этой линии проводят прямые, касательные к ее крайним точкам. Наикратчайшее расстояние между ними будет шириной полосы . Шаг подачи материала равен расстоянию между полюсами деталей. Последовательно производятся такие же действия по всем остальным критическим точкам. Для каждой точки вычисляют произведение шага на ширину полосы, т. е. минимальную площадь прямоугольника для наиболее плотного размещения заготовок.

На втором этапе деталь описывается выпуклым многоугольником (рис.8.8в), одна сторона которого совещается с краем полосы. Затем параллельно ей проводится линия из полюса детали до пересечения с годографом (шаг подачи ) и касательная к крайней точке детали (ширина полосы ). Площади прямоугольников определяются при последовательном совмещении сторон указанного выше прямоугольника с краем полосы. Полученные на 1 и 2 этапах построений значения площадей сравнивают и определяют вариант с минимальной площадью, для которого определяется угол наклона деталей к направлению подачи. При построении многорядного размещения деталей достаточно ограничится рассмотрением оптимального размещения деталей в один ряд, а последующие ряды размещать с одинаковым углом наклона деталей к направлению подачи или повернутым на . Конфигурация некоторых деталей позволяет смещать последующие ряды относительно предыдущих и получать при этом наиболее плотное заполнение площади материала. Коэффициент использования материала

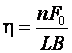
Где площадь детали, число рядов.

На ряде предприятий созданы и успешно работают системы проектирования «Автоштамп», с помощью которых решается задача выбора оптимальной схемы раскроя при многорядной штамповке. Автоматизированный выбор такой схемы производится только для типовых деталей и предусматривает несколько вариантов раскроя: однорядный, многорядный (2 – 3-х рядный) и встречный (прямой и наклонный).

Обработка рулона и листа на листоштамповочных с комплексах реализацией оптимального раскроя образуется путем двух перемещений, которые обеспечиваются конструкцией механизма для многорядной штамповки синхронно связанного с движением ползуна пресса.

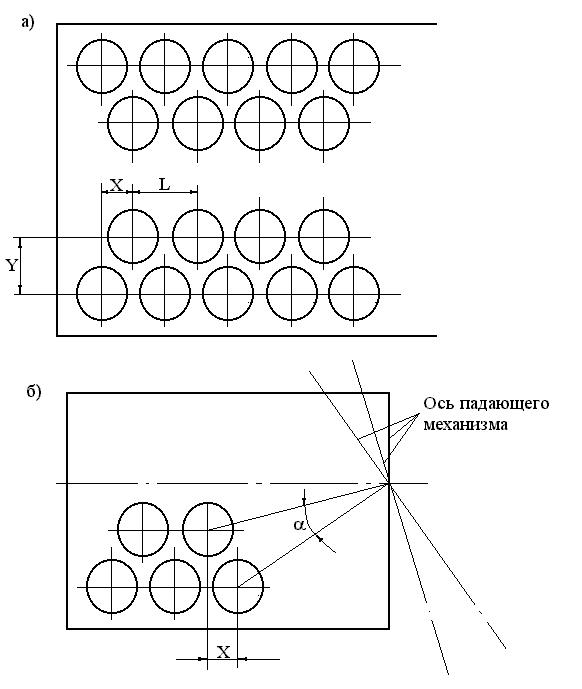
Рис. 8.9 Способы оптимального раскроя: а - взаимноперпендикулярное перемещение координат Х,Y; б - перемещение координаты Х относительно полосы.

Известны два способа оптимального раскроя. Первый способ достигается в результате двух взаимноперпендикулярных перемещений полюса вырубленной детали относительно полюса контура предыдущей вырубаемой детали (рис.8.9а). Второй способ заключается в перемещении и повороте на угол полюса последующей вырубки (рис.8.9б). Регулировочные перемещения или влияющие на оптимальный раскрой материала, необходимо определять не только в процессе наладки, но и при проектировании механизмов перемещения.

Условимся, что под лекальными кривыми будем понимать все линии, форма которых аппроксимируется полиномами второго порядка и выше. К деталям, имеющим правильную геометрическую форму, отнесем фигуры, образуемые кривыми одного порядка. Они могут быть получены пересечением прямых линий, очерчены окружностью, эллипсом и т. д. К фигурам, образованным прямыми линиями, относятся треугольники, прямоугольники, трапеции, правильные многоугольники.

Фигуры называются разделяющимися, если найдутся такие полюса для которых плотное размещение этих фигур таково, что они не пересекаются при перемещении их вдоль линии, соединяющей полюса, в противоположные стороны. В противном случае фигуры называются неразделяющимися. Выпуклые фигуры являются неразделяющимися. Существующие метатические методы определения функции плотного размещения распространяются на разделяющиеся фигуры. Под функцией плотного размещения взаимно ориентированных фигур и понимается зависимость расстояния между полюсами и фигур от угла их поворота при условии, что фигуры касаются, но не пересекаются и не накладываются друг на друга. При функция непрерывна и однозначна. В общем случае ; Опорная функция определяет зависимость расстояний между полюсом фигуры и опорной прямой от угла поворота фигуры при неподвижной опорной прямой. Составная опорная функция . Область определения и свойства опорной функции аналогичны области и свойствам функции .

Перемещение фигур вдоль параллельных линий, проходящих через их полюса, при условии их взаимного касания определяет периодичность размещения фигур. При этом расстояние между их полюсами есть шаг штамповки , который при поиске размещения зависит от угла поворота фигуры .

Задача нахождения более выгодного варианта размещения фигур на полосе заключается в нахождении параллелограмма наименьшей площади, в которой можно заключить фигуру. Длина основания параллелограмма является шагом перемещения фигуры (шаг штамповки). Площадь параллелограмма складывается из площадей параллелограммов, основания которых есть шаг штамповки, а высота определяется опорными функциями плотного размещения при многорядном размещении фигур.

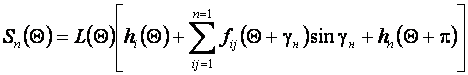(8.26)

Где угол наклона фигур к направлению подачи материала, принимаемый равным для всех рядов штампуемых деталей.

Функция , определяющая минимальную площадь параллелограмма, является функцией цели при поиске оптимального раскроя материала.

Анализ функции цели на экстремальность дает возможность выделить такое положение фигур, при котором возможны экстремумы функции цели. Поиск экстремума сводится к решению двух уравнений.

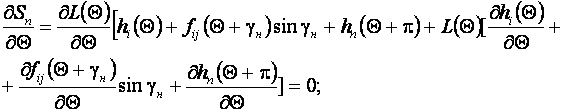(8.27)

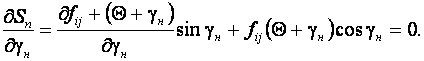
При проектировании схемы раскроя, которая реализуется на листоштамповочных комплексах для многорядного раскроя, необходимо определять два перемещения и или и . Они зависят от функции плотного размещения фигур и от угла их наклона к направлению подачи:

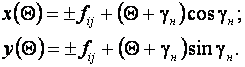(8.28)

Знак (-) соответствует перемещению в направлении противоположном направлению подачи материала.

При штамповке деталей повторяющимися параллельными рядами значения и повторяются от ряда к ряду, поэтому достаточно их определить для двухрядного раскроя, а координаты полюсов деталей последующих рядов определять чередованием знаков при перемещении. Для двухрядной схемы раскроя система уравнений (8.27) упрощается, решая ее находят перемещение материала:

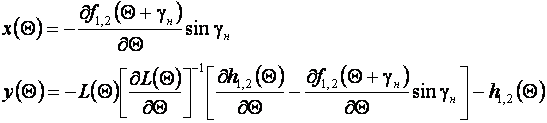(8.29)

Система уравнений (8.29) позволяет выбрать значения , удовлетворяющие условию оптимального раскроя. При этом значения должны совпадать с рассчитанными по уравнению (8.29) для одинаковых значений углов и , удовлетворяющий условию плотного размещения, используется при проектировании штампа и определяет наклон оси детали к направлению подачи материала.

Угол поворота материала легко найти из уравнения (8.28) и (8.29), согласно которым оптимальный раскрой зависит от угла наклона детали к направлению подачи

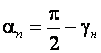(8.30)

Определение , , и из уравнений (8.28) – (8.30) возможно путем их численного решения на ЭВМ, при этом контур детали разбивается на отрезки прямых и лекальных линий. Полюс детали выбирается на пересечении диагоналей параллелограмма, описывающего деталь. В системе координат с центром в полюсе детали задаются точки, описывающие ее форму. Отрезки задаются двумя точками, лекальные кривые – тремя. Для учета технологических перемычек при штамповке координаты точек определяются по эквидистантной линии, описанной вокруг детали и удаленной от ее контура на половину перемычки.