Для анализа механических и элек­тромеханических колебательных систем широко пользуются методом электро­механических аналогий [59, 90, 224, 300]. Он основан на сходстве дифференциаль­ных уравнений, описывающих колебания электрических и механических систем. Главное достоинство метода - возможность применения хорошо разработанных спосо­бов анализа электрических цепей к расчету механических колебательных систем.

Основные элементы механических колебательных систем с сосредоточенны­ми постоянными - масса т, гибкость К и активное сопротивление R. Гибкость представляет собой величину, обратную жесткости. В литературе используют так­же эквивалентные гибкости термины: податливость, сжимаемость, упругость. Параметры механических колебательных систем с распределенными постоянными - волновое сопротивление W = Spc, посто­янная распространения у = 5 + jk, геомет­рические размеры и форма (в частности, для стержня длина /). Элементы электри­ческих цепей с сосредоточенными посто­янными - индуктивность L, емкость С и активное сопротивление R. Основные па­раметры электрических цепей с распреде­ленными постоянными (длинных линий) -

волновое сопротивление % =Jl0/C0

(Lo и Со - индуктивность и емкость линии на единицу ее длины), постоянная распро­странения у и длина /.

Отметим, что при выводе уравнения распространения упругой волны в стержне волновое сопротивление последнего также

представляется в виде W = ^jm0/K0 , где т0иКо~ масса и гибкость стержня на еди-

.16. Условные оозначения механических и электрических элементов

Механические элементы

Электрические элементы

Масса	Индуктивность
т
Г ибкость	Емкость
ft
Активное сопротивление	Активное сопротивление
R CZb
R

 

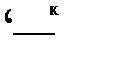Электрический

импеданс

Система с распре­деленными посто­янными (стержень)

ницу длины. Таким образом, структура выражений для W и ^ одинакова. Поэтому существует полная аналогия между вол­новыми сопротивлениями для электрической линии и продольно колеблющегося стержня. Такое же соот­ветствие имеется между постоянными распространения электрической и механи­ческой систем с распределенными посто­янными.

В методе электромеханических ана­логий упругую составляющую механиче­ского импеданса представляют гибко­стью, так как ее электрическим аналогом служит емкость.

Условные обозначения элементов механических и электрических систем показаны в табл. 1.16. Если неясно, о ка­кой составляющей импеданса идет речь, электрические элементы снабжают индек­
сом "Е", механические - "М".

Используя аналогии механических и электрических элементов (табл. 1.17), со­ставляют эквивалентную схему (иначе схему замещения) механической системы и анализируют ее известными методами теории цепей. Это особенно удобно при расчете сложных механических и элек­тромеханических систем с несколькими степенями свободы.

Метод электромеханических анало­гий применим к системам, содержащим элементы с сосредоточенными и распре­деленными постоянными, а также к ком­бинированным системам, включающим в себя те и другие элементы. Кроме того, сама структура эквивалентной схемы по­могает качественно оценить поведение анализируемой системы в различных ус­ловиях (например, при различных нагруз-

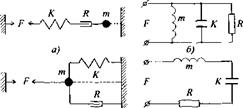
в) г) Рис. 1.77. Механические двухполюсники и их эквивалентные схемы: а - соединение элементов цепочкой; б - эквивалентная схема для соединения цепочкой; в - соединение элементов узлом; г - эквивалентная схема для соединения узлом

ках). На эквивалентных схемах механиче­ские элементы обозначают так же, как их электрические аналоги, за исключением буквенных символов.

Эквивалентные схемы механических систем составляют по определенным пра­вилам. Так, механические двухполюсники, на все элементы которых действует оди­наковая сила F (рис. 1.77, а), называют соединенными цепочкой. Это соответству­ет параллельному соединению на схеме замещения (рис. 1.77, б), когда колеба­тельные скорости всех элементов различ­ны. Резонанс в соединенном цепочкой т, К, R двухполюснике называют резонансом скоростей, что соответствует резонансу токов в параллельном электрическом кон­туре. В приведенном ранее смысле резо­нанс скоростей является антирезонансом, так как при этом Хш = 0, а активная со­ставляющая механического импеданса максимальна.

Двухполюсники, элементы которых обладают одинаковой колебательной ско­ростью (рис. 1.77, в), называют соединен­ными узлом, что соответствует последова­тельному соединению на эквивалентной схеме (рис. 1.77, г). В этом случае на эле­менты двухполюсника действуют разные силы. Резонанс в механическом двухпо­люснике т, К, R с элементами, соединен­ными узлом, именуют резонансом сил. Это соответствует резонансу напряжений в последовательном электрическом контуре. При резонансе сил реактивная состав­ляющая входного импеданса равна нулю, а активная минимальна.

При непосредственном (без проме­жуточных активных или упругих сопро­тивлений) соединении и инерционных элементов (например, масс тх, т2, тъ, ..., т„) их массы складывают: М = тх + т2+ + /и3 + ... + т„. Элемент М массы рассмат­ривается как материальная точка, смеще­ние и колебательная скорость которой в каждый момент времени имеют единст­венные значения, отсчитываемые в непод­вижной системе координат. Таким обра­зом, соединение масс возможно только узлом.

В отличие от элемента массы под смещениями и колебательными скоростя­ми активного сопротивления и гибкости понимают разности соответствующих параметров на концах этих элементов.

При непосредственном соединении упругих элементов, обладающих гибко­стями К и К2, возможно их соединение как узлом, так и цепочкой. При соедине­нии узлом два конца одного элемента со­единены с двумя концами другого. Сме­щения и колебательные скорости обоих элементов, равные разностям этих пара­метров на концах объединенного элемен­та, соответственно равны. При этом гиб­кость К результирующего упругого сопро­тивления меньше гибкостей К и К2 его составляющих. Величина К определяется формулой К— КХК2/(КХ + К2). В случае со­единения и гибкостей узлом результи­рующая гибкость вычисляется из выраже­ния

_L-_L _J_ _L J_

K~KX К2+ К3 "X '

При соединении и гибкостей цепоч­кой результирующая гибкость

К = КХ +К2 + К3+ ... + К„.

Таким образом, соединение гибко­стей узлом подобно последовательному соединению электрических конденсато­ров, соединение цепочкой - параллельно­му.

1.17. Электрические и механические аналоги Электрические величины Механические величины Заряд q Смещение и Ток і = dq/dt Колебательная скорость v = du/dt Скорость изменения тока dildt = d2q/dt2 Ускорение dv/dt - cf uldt2 Напряжение U Сила і7 Емкость С Гибкость К Индуктивность L Масса т Активное электрическое сопротивление R Активное механическое сопротивление R Емкостное сопротивление 1/уюС Упругое сопротивление l/j(oK Индуктивное сопротивление jab Инерционное сопротивление jam Идеальный (без потерь) трансформатор с коэффициентом трансформации и Абсолютно жесткий и невесомый рычаг с соотношением плеч п = 1]/12 Волновое сопротивление длинной линии.__ * р= £ і Со Волновое сопротивление стержня Ш=р cS Эквивалентный ген С ератор напряжения ——-о — о Эквивалентный ге с нератор силы о —- '-О Эквивалентный гет іератор тока f О Эквивалентный г ной скорости <? енератор колебатель- * L0 и С0 - индуктивность и емкость на единицу длины линии.

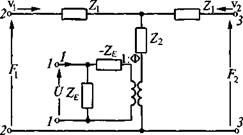
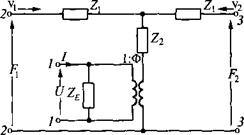
Рис. 1.78. Эквивалентная схема пьезоэлемента, колеблющегося по толщине (продольный пьезоэффект)

Метод электромеханических анало­гий применим также для расчетов элек­тромеханических преобразователей (пье­зоэлементов, микро - и гидрофонов И Т. П.), имеющих две стороны: электрическую и механическую (акустическую). В режиме излучения такой преобразователь транс­формирует подводимую электрическую энергию в механическую, в режиме прие­ма - механическую энергию в электриче­скую.

Механическую и электрическую сто­роны преобразователя соединяют элек­тромеханическими трансформаторами. Одна сторона ("обмотка") такого транс­форматора соединена с электрическими, другая - с механическими элементами схемы замещения. Параметры электроме­ханического трансформатора выражают через константы преобразователя.

Для расчета различных типов пьезо­преобразователей пользуются их эквива­лентными схемами, основанными на схе­мах замещения пьезоэлементов. Наиболее полные схемы замещения пьезоэлементов в виде шестиполюсников с одной элек­трической и двумя механическими сторо­нами разработаны независимо друг от друга Л. Я. Гутиным [112] и У. Мэзоном [384]. Эти и другие подобные схемы опи­саны в многочисленных монографиях и статьях [127,141].

Известно несколько типов пьеэоэле- ментов, отличающихся характером коле­баний. В дефектоскопии применяют в ос­новном пьезоэлементы в виде колеблю­щейся по толщине пластины и (реже) - длинного бруска прямоугольного сечения с электродами на боковых сторонах, со­вершающего продольные колебания.

На рис. 1.78 приведена эквивалент­ная схема пьезоэлемента в форме колеб­лющейся по толщине пластины, направле­ние поляризации которой совпадает с на­правлением колебаний (продольный пье­зоэффект). Зажимы 1-1 соединены с элек­трической схемой (генератором, усилите­лем). На электрической стороне пьезоэле­мента действует напряжение U и протека­ет ток I. Зажимы 2—2 и 3-3 отображают переднюю и заднюю поверхности пьезо­элемента, на которых действуют силы F, F2 и колебательные скорости vb v2 соот­ветственно.

Импеданс (-ZE) имеет чисто расчет­ный характер. Он учитывается только для пьезоэлементов с большим коэффициен­том электромеханической связи [3. Для кварцевых пьезоэлементов (Р < 0,1) этим импедансом пренебрегают. Электрическая и механическая стороны схемы связаны через идеальный (без потерь) электроме­ханический трансформатор с коэффици­ентом трансформации 1: Ф.

Для широкой пьезопластины (d » /.) параметры схемы следующие [28]: ZE = = 1/усо Сд ; Со = Ве!,/1 = ВеТ33 (1 - р,2)//, где Со - емкость зажатого пьезоэлемента; В - площадь электрода пьезопластины; / - ее толщина; е33 и Є33 - диэлектриче­ские проницаемости зажатого и свободно­го пьезоэлементов соответственно; Р, - коэффициент электромеханической связи (см. разд. 1.2.3) для продольных ко­лебаний широкой пьезопластины; Z = = lTth(y//2), Z2 = W/sh(yl), где W = BpcD - волновое сопротивление пьезоэлемента; у = 8 + jk — постоянная распространения (к = <а/с° - волновое число, р - плотность, с° = (с: зз/р)12 - скорость продольной вол­ны в пьезоэлектрике с разомкнутой элек­трической цепью, где Су} - упругая по­стоянная пьезоэлектрика для того же слу­чая); Ф = В$,( Е'зз Сзз )1/2// - коэффициент трансформации.

Для пьезоэлемента в виде узкого стержня с электродами на торцевых по­верхностях схема остается той же, но ме­няется коэффициент электромеханической связи, который обозначается р33.

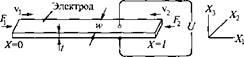
Эквивалентная схема для показанно­го на рис. 1.79 пьезоэлемента в виде бру­ска прямоугольного сечения с электрода­ми на боковых сторонах (поперечный пьезоэффект) приведена на рис. 1.80. Им­педанс (-ZE) в ней отсутствует. Схема имеет следующие параметры: ZE =

= I//® СЕ ; Cq = А 4 (1 - (Зз2, )/t = А в?, Н

[Сд - емкость зажатого пьезоэлемента;

А = wl - площадь электрода, где w - его ширина, / - длина; t - расстояние между электродами; Z; = ИЛ1і(у//2); Z2 =

= H7sh(y/), где W = wtpcE - волновое со­противление; у = 5 + jk - постоянная рас­пространения (к = со/сЕ - волновое число); сЕ = (с,£, /р)1/2 - скорость звука для пьезо­элемента с короткозамкнутой электриче­ской цепью, где 4 - упругая постоянная

для того же случая; Ф = тсрз^є^ 4 )|/2 -

коэффициент трансформации (р3і - коэф­фициент электромеханической связи для поперечного пьезоэффекта).

Если не учитывать потери в пъезо- элементе, то в обеих схемах замещения принимают Zj = jWtg(kl/2) и Z2= W/jsin(kl).

Поясним обозначения параметров рассмотренных эквивалентных схем. Электрические параметры характеризуют­ся диэлектрической проницаемостью, механические - плотностью и постоянны­ми упругости. Электрические и механиче­ские параметры взаимосвязаны тем силь­нее, чем больше коэффициент электроме­ханической связи р. Значения пьезоэлек-

/ Рис. 1.79. Продольио-колеблющийся пьезоэлемент с электродами на боковых сторонах

трических параметров определяются так­же характером (модой) колебаний пьезо­элемента.

В обозначениях пьезоэлектрических параметров используют буквенные и циф­ровые индексы. Верхний буквенный ин­декс указывает величину, постоянную при его определении: Т - механическое на­пряжение, S - деформацию, Е - напря­женность электрического поля, D - ди­электрическое смещение. Индексы S и Т относятся к электрическим параметрам, Е и D - к механическим. Первый нижний цифровой индекс характеризует направле­ние электрического поля, второй - меха­нического напряжения.

Диэлектрические проницаемости. Параметр є33 диэлектрическая проницае­мость для продольного пьезоэффекта при постоянстве механического напряжения. Вектор электрического поля совпадает с направлением механического напряжения (продольный пьезоэффект). Постоянство механических напряжений (равен-

Рис. 1.80. Эквивалентная схема пьезоэлемента в виде бруска с электродами на боковых сторонах (поперечный пьезоэффект)

1.18. Параметры пьезокерамики отечественной и британской Параметр Пьезокерамика ЦТС-19 PZT-4 Скорость звука с°, м/с 4240 4600 Плотность р, кг/м3 7330 7500 Постоянная упругости, ГПа: 4 132 159 4 - 145 4 - 115 Волновое сопротивление z = р с°, МПа с/м 31,08 34,5 Добротность свободного элемента Q 70 500 Коэффициент электромеханической СВЯЗИ для* широкой пластины (продоль­ный пьезоэффект) (3, 0,44 0,51 стержня (продольный пьезоэф­фект) рзз 0,61 0,7 стержня (поперечный пьезоэф­фект) рз, 0,31 0,33 Относительная диэлектрическая про- ницаемость для: широкой пластины (продоль­ный пьезоэффект) Єзз/Єо 935 635 стержня (продольный пьезоэф­фект) 833/в0 976 663 стержня (поперечный пьезоэф­фект) вц/8о - 730

ство их нулю) обеспечивается при свобод­ных гранях пьезоэлемента. Значение 833 находят измерением емкости свободного пьезоэлемента на низких частотах (100 ... 1000 Гц), далеких от его собственных час­тот.

Параметр ef3 = Є33 (1 - р|3) — ди­электрическая проницаемость при посто­янстве деформации для тех же направле­ний поля и механических напряжений. Это соответствует жесткому закреплению граней пьезоэлемента, исключающему его деформацию при воздействии поля. Пара - метр є33 расчетная величина, так как практическая реализация условий жестко­го закрепления затруднительна.

Для пьезоэлемента в виде тонкого (по сравнению с длиной волны) стержня с электродами на торцах вместо (3, (для ши­рокой пластины) используют значение р33.

о

Для поперечного пьезоэффекта є31 =

= 4з (1 - Рз, )•

Упругие постоянные пьезоэлемента с разомкнутой электрической цепью име­ют верхний индекс D (постоянная индук­ция), с короткозамкнутой цепью - индекс Е (постоянная напряженность поля Е = 0). Так, Су} - постоянная упругости пьезо­элемента с разомкнутой электрической цепью для продольного пьезоэффекта, когда вектор поля совпадает с направле­нием деформации.

Известны эквивалентные схемы так­же других типов пьезоэлементов и иных электромеханических преобразователей.

В отечественной литературе сведения о пьезоэлектричеких параметрах, необхо­димых для расчета преобразователей, приведены очень скупо. Даже в ГОСТ 13927-68 значения диэлектрических про­ницаемостей, постоянных упругости и других констант приведены без указания, к каким условиям они относятся. Кроме того, эти значения имеют большой раз­брос. В переводной и оригинальной ино­странной литературе можно найти данные

гУФ

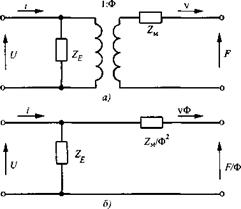
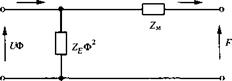
в) Рис. 1.81. Эквивалентная схема с электромеханическим трансформатором (а) и та же схема, пересчитанная на электрическую (б) и механическую (в) стороны

только о материалах зарубежного произ­водства.

Некоторые параметры наиболее рас­пространенной отечественной пьезокера­мики ЦТС-19, по данным [127, 141] (более подробно, чем в табл. 1.7), и керамики PZT-4 британской фирмы Vemitron при­ведены в табл. 1.18.

Параметры электрической стороны схемы замещения можно пересчитывать на механическую сторону и наоборот, т. е. приводить систему к одной ее стороне. Электрические напряжения пересчитыва­ют в силы на механической стороне ум­ножением на коэффициент трансформа­ции Ф, токи в колебательные скорости - делением на Ф, электрические импедансы (в механические) - умножением на Ф2. Аналогично пересчитывают параметры механической стороны на электрическую сторону.

В качестве примера на рис. 1.81, а показана эквивалентная схема электроме­

ханической системы. На ее электрической стороне действует напряжение U, проте­кает ток і и включен электрический импе­данс Ze - Механическая сторона представ­лена механическим импедансом ZM, силой F и колебательной скоростью v.

После приведения к электрической стороне схема приобретает вид рис. 1.81,

б. Аналогично схема, изображенная на рис. 1.81, а, приводится к механической стороне (рис. 1.81, в). Указанные преобра­зования эквивалентных схем упрощают анализ. Выбор стороны, к которой приво­дится схема, произволен и диктуется со­ображениями удобства.

Эквивалентные схемы полезны не только для численных расчетов. Часто они позволяют и качественно оценить поведе­ние пьезоэлемента в различных режимах.

Например, если правая сторона схе­мы, показанной на рис. 1.78, соединена с полезной акустической нагрузкой, а тыль­ная (на схеме левая) сторона пьезоэлемен­та свободна (т. е. закорочена, так как Z = = Fh = 0), то передача энергии в нагруз­ку будет мала вследствие шунтирующего влияния левой части схемы. Если же на­грузить тыльную сторону на очень боль­шое сопротивление, то это влияние устра­нится и передача энергии в полезную на­грузку резко возрастет.

Метод электромеханических анало­гий широко применяют также для расчета других механических и электромеханиче­ских колебательных систем.