ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ТЕПЛООБМЕНА
 23 марта, 2013
23 марта, 2013  admin
admin Аналитическое исследование процессов теплообмена связано с изучением пространственно-временного распределения температуры
T = F(X, у, Z, т).
В общем случае теплообмен определяется не только тепловыми, но и гидродинамическими явлениями, поэтому математическое описание процесса включает систему дифференциальных уравнений, в которые входят уравнение энергии, уравнение движения и уравнение сплошности.
|
(2.11) |
Аналитические методы позволяют вскрыть физические особенности и общие принципиальные закономерности процессов теплообмена.
Дифференциальное уравнение энергии. Дифференциальное уравнение энергии выводится на основе первого закона термодинамики. Для единицы объема потока рабочего тела в условиях теплообмена он может быть записан в следующем виде:
Qdx + Ldx = Pdu + (2.13)
Где Q — количество теплоты, подведенное к единице объема потока в единицу времени, Дж/(м3-с); L — работа, совершаемая внешними силами над единицей объема в единицу времени, Дж/(м3-с); р — плотность, кг/м3; и — внутренняя энергия среды, Дж/кг; w — скорость движения среды, м/с.
Как было показано в первой главе, внутренняя энергия связана с энтальпией соотношением H = и + Pv. Тогда
Du = Dh - D(ро) = Dh - = Dh -+ P~2PdP. (2.14)
В процессе теплообмена работой L внешних сил можно пренебречь. Определим Q. Для этого с помощью контрольной поверхности выделим в теле произвольный объем V и тепловое воздействие части тела за пределами этого объема заменим некоторым распределением вектора Q по поверхности F объема.
Уравнение теплового баланса этого объема, отнесенное к единице времени, можно записать
QdV+ $qdF = qvdV, (2.15)
V F V
Где Q0 — мощность внутренних источников теплоты, Вт/м3.
В соответствии с теоремой Гаусса — Остроградского между потоком вектора через поверхность ґ, ограничивающую объем V, и дивергенцией вектора существует связь
J qdF = fdiv<?dK
F V
Подставим это выражение в уравнение (2.15) QdV+ JdivgdK= Jg„dK
V V V
Откуда
Q — Qv~ div Q. (2.16)
Подставим найденное выражение Q (2.16) и Du (2.14) в уравнение первого закона термодинамики (2.13):
D (—
,. Dh dp р Dp I 2 ,
Qv - div q = P —----- j - 4- — + p y, 2.17)
DT Dx p dx dx
Где
Ox dy oz
Считая в соответствии с законом Фурье
|
Divg- ~XV2T, |
, 8T Dt Dt
Получим при постоянной теплопроводности
82t D2T дН
Дх2 ду2 Dz
D2T D2T D2T Где V2T = -—— 4- —5- + — оператор Лапласа. Дх2 Ду2 DzM
Уравнение (2.17) с учетом полученного выражения divg будет:
+ але)
Dt dx р Dt dx
В условиях теплообмена при умеренных скоростях теплоносителя кинетической энергией и изменением давления можно пренебречь. Тогда, считая плотность среды постоянной, получим дифференциальное уравнение энергии в следующем виде:
Dh
C]V + ^T = P—. (2.19)
Подставим Dh = тогда получим уравнение энергии в виде
Qv + XV2T = рс„ или ~ = V2f + —, (2.20)
' dx dx рср
Где а = Х/рСр — коэффициент температуропроводности, м2/с.
Величина а, так же как X, ср и р, является физической константой вещества и характеризует скорость изменения температуры. Например, как видно из уравнения (2.20), при отсутствии внутренних источников теплоты Qv = 0, скорость изменения температуры зависит только от коэффициента температуропроводности. Выравнивание температур в теле будет достигаться тем быстрее, чем выше значение а.
Полная производная температуры по времени равна
AL - 1L lLdx lL(lL J! Li! L - 1L ^L Лі. Лі
Dx Дх дх Dx Dy Dx Dz Dx Dx X Dx Y Dy Z Dz'
(2.21)
Dt „
Частная производная — называется локальной производной темпе-
Dt Dt Dt Ратуры, а величина wv 1-wv——I - vv„ — конвективной производ-
' Dx Dy ' Dz
Ной. Так как производная связана с движущейся средой (субстанцией), ее называют субстанциональной производной и обозначают Dt_ Dx '
Уравнение, энергии (2.20) при этом будет
|
|
Для твердого тела wx = wy = wz = 0 и конвективной составляющей субстанциональной производной можно пренебречь, тогда при ср = с Уравнение (2.22) принимает вид:
|
|
|
Jh рс |
(2.23)
При отсутствии внутренних источников теплоты уравнение (2.23) упрощается и принимает вид
|
|
(2.24)
Уравнения (2.23) и (2.24) называются дифференциальными уравнениями теплопроводности.
Уравнение движения. В гидродинамике для вывода основного уравнения движения жидкости используется второй закон механики Ньютона: масса х ускорение = сумме сил, действующих на тело.
Выделим из потока жидкости элементарный объем dF = d. xdydz. Масса его равна PdV, где р — плотность жидкости.
|
|
|
|
|
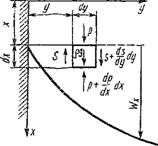
Рис. 2.3. К выводу уравнения движения |
В общем случае на элемент DV действуют следующие силы: сила тяжести, сила давления (обусловленная распределением давления вокруг элемента DV) и сила трения (обусловленная вязкостью жидкости). Найдем проекции этих сил на ось л* (рис. 2.3): сила тяжести
(2.25)
Равнодействующая сил давления
(2.26)
Равнодействующая сил трения
(2.27)
Выразим S по закону трения Ньютона 5 = (.L Dwjdy И принимая р. — динамическую вязкость, Н • с/м2, постоянной, получим
®.d (2.28)
Теперь подставим найденные силы в формулу второго закона механики Ньютона, сократим на DV и получим выражение
|
|
В неизотермических условиях необходимо ввести поправку на подъемные силы, возникающие вследствие разности плотностей горячих и холодных частей жидкости. Выразим зависимость плотности жидкости от температуры через коэффициент объемного расширения 0 = = (Ро — p)/[Po (t — *о)]> и считая J3 постоянным, получим равнодействующую сил тяжести в следующем виде:
РОх = Ро [1 - Р (t - To)] дх = роДх - Pop (t - To) дх, (2.30)
Где T, T0 — температуры, соответствующие плотностям р и р0.
Для многих задач конвективного теплообмена можно с достаточной степенью точности ограничиться только подъемной составляющей: считая р расчетным значением плотности и обозначив T — T0 — получим ее выражение: рР%ух.
С учетом этих поправок уравнение движения примет вид
®WX Dp д2и.
+ С-3"
Найдем полную производную:
Dwx = Dwx | Dwx dx ] Dwx dy [ Dvt^ dz Dx дх дх дх ду дх Dz дх'
Или
Dwx Dwx Dwx Dwx Dwx
~DГ = + + (Z33)
Для трехмерного движения равнодействующая сил вязкого трения определяется выражением:
B2yf* ■ D*W* ■ D2Wx .
"а/ + = й <2-34>
Где V2Wx — оператор Лапласа.
В развернутом виде дифференциальное уравнение движения в проекции на ось х получает вид
Dwx dwx dwx dwx _ . 1 Dp
+ -^--w, + u', + —IWjs = Gx$At-------------------- / + W4, 2.35
Dx dx dy y dz p йх
Где v = fi/p — кинематическая вязкость, м2/с.
Аналогично могут быть получены уравнения проекций равнодействующих сил на оси у и г.
В векторной форме дифференциальное уравнение движения имеет вид
Dw п А 1 _
-— = At--------------- Vp + v V2tf.
Dx p
Система уравнений (2.22) и (2.35) не замкнута, так как содержит три неизвестных w и р. Уравнением, необходимым для замыкания системы, является уравнение сплошности.
Уравнение сплошности. Выделим в потоке жидкости (рис. 2.4) элементарный объем DV = Dxdydz. В направлении х за время dx втекает масса dМх = (pvvx)dydzdx. Из противоположной грани вытекает
Pw.+ ii^ldx Dx
Лишек массы, вытекающей из элементарного объема по оси х, будет:
|
D Mx |
|
Dydzdx. Из- |
|
+ d* |
|
DM, |
|
4+dz |
|
Ш, |
|
DM, |
|
DM; |
|
J----- |
|
V |
Дх
|
Z. |
|
7 |
|
DM, |
|
_ д(рWy) |
|
DM |
|
DM, |
|
Y + dy |
|
1 |
Аналогично, по оси у
DMv = dFdx;
By
По оси Z
Рис. 2.4. К выводу уравнения сплошности
DMs + ds - dMz = ll^LdKdx.
Dz
Суммируя, получим избыток массы
D(png d(pwy) Д (pwz)
|
(2.37) |
"Г--- г------ 1"
Dx Dy Dz
Который может быть выражен изменением плотности
|
DM = |
|
(2.36) |
|
DKdx, |
DМ = - ~DVdx. дх
|
(2.38) |
Приравнивая (2.36) и (2.37), получаем уравнение сплошности или уравнение сохранения массы в виде
Dp д(рн'х) | Д (Pwy) д (Pwg) = 0
Dx Dx ду Dz
Считая для несжимаемой жидкости р = const и др/<3т = 0, получаем в окончательном виде
Dwx Dwv --------- L.
|
<3w„ |
|
(2.39) |
Дх ду
Или в векторной форме: div w = 0.
Приведенная система дифференциальных уравнений (2.22), (2.35) и (2.39) описывает целый класс явлений теплообмена и имеет бесчисленное число решений. Чтобы выделить конкретное явление из множества явлений, описываемых уравнениями (2.22), (2.35), (2.39), необходимо дополнительно задать условия однозначности, которые включают в себя:
Геометрические условия, характеризующие форму и размеры тела; Физические условия, характеризующие физические свойства среды или системы;
Начальные условия, характеризующие особенности протекания нестационарных процессов в определенный обычно начальный момент времени;
Граничные условия, характеризующие условия протекания процесса на границах тела или системы. Подробнее о задании граничных условий указано в § 2.4.
Решение системы дифференциальных уравнений теплообмена средствами математического анализа связано с большими, иногда непреодолимыми трудностями. Аналитические решения удается получить лишь для некоторых частных случаев при условии введения упрощающих предпосылок. Поэтому такие задачи решаются либо численными методами с использованием вычислительной техники, либо для исследования теплообмена используются экспериментальные методы. Численные и экспериментальные результаты представляют собой решения отдельных частных задач, обобщение которых ограничено. При изменении каждого из аргументов требуется новое решение или новый эксперимент. Преодолеть эти трудности позволяет теория подобия.

 Опубликовано в
Опубликовано в