Аналитические методы
 28 ноября, 2012
28 ноября, 2012  admin
admin Поведение полученных намоткой волокном композитов аналогично поведению других типов слоистых материалов с расположенными под углом слоями армирующих компонентов. Поэтому разработанные для них аналитические методы могут быть использованы и для конструкций, получаемых намоткой. При рассмотрении этого вопроса с позиций макромеханики анализ композитов базируется на предположении, что каждый слой является анизотропным гомогенным монослоем. Монослой состоит из волокон, ориентированных под углом ±<х или однонаправленных. Свойства монослоя обычно определяют экспериментальным путем, и анализ структуры строится путем перехода от одного слоя к другому. Микромеханический подход, наоборот, заключается в исследовании характеристик чувствительности составных частей материала, т. е. распределения напряжений и деформаций между армирующими волокнами и матрицей. При определении напряжений и деформаций по точкам принимают во внимание свойства армирующего материала и смолы, а также геометрию изделия. Этот анализ микронапряжений устанавливает, какие нагрузки может выдержать композит перед переходом через предел текучести в какой-то точке или перед достижением критических напряжений. Микромеханический подход применяется также для расчета характеристик композиционного материала по известным их значениям для входящих в его состав компонентов, а также для установления влияния их изменения на соответствующие свойства композита.
Оба метода расчета рассмотрены в других главах этого справочника. Дополнительные данные, касающиеся непосредственно получаемых намоткой волокном цилиндров, можно найти в литературе [14, 19—21].
|
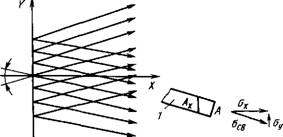
Рис. 16.16. Ориентация волокна при анализе с помощью метода сеток: I — одинарное волокно |
|
А а |
|
8* |
|
227 |
Анализ переплетений представляет собой упрощенную процедуру, применяемую, главным образом, для определения напря
жений в волокнах цилиндрических сосудов, находящихся под внутренним давлением. Этот метод основан на допущениях, что несущей способностью обладает только армирующее волокно и что все волокна нагружены равномерно. На рис. 16.16 изображена двухслойная система из параллельных волокон, для которой можно вывести уравнения переплетений.
Обозначим напряжение, приходящееся на площадь поперечного сечения каждого стекловолокна, асв. Действующие силы можно разложить на составляющие по осям X и Y, соответствующим окружному и продольному направлениям соответственно. Суммирование сил fro обоим направлениям приводит к следующим уравнениям:
Ох = (Усв cos2 а; (16.11)
<*у = 0СВ sin2 а; (16.12)
<Jy/ox = tg2a, (16.13)
Где а — угол намотки.
Если конструкция состоит из двух слоев, намотанных под разными углами, можно вывести следующие выражения.
Продольное направление:
Апр + t2) = oJx cos2 а + a2t2 cos2 а. (16.14)
Окружное направление:
TfOKp (k + Q = Mi sin2 аг + a2t2 sin2 а2. (16.15)
Когда наружный слой состоит только из окружных намоток, уравнения (16.14) и (16.15) упрощаются:
СтПр^1 = Mi cos2 (16.16)
TfOKp + = Mi sin2 + о2І2, (16.17)
Где апр — продольное напряжение; аокр — окружное напряжение; — напряжение в волокне сЛоя 1; аа — напряжение в волокне слоя 2; tx и t2 — толщина слоев 1 и 2; аг и а2 — углы намотки слоев 1 и 2.
Обычно ах = аа = асв. Тогда отношение толщин, полученных окружной (fOKp) и спиральной (4п) намоткой, в закрытом сосуде высокого давления можно выразить с помощью уравнения
= 2 cos2 <*! - sin2= 3 cos2 ax - 1. (16.18)
'СП
Модуль упругости Е в направлении волокна и коэффициент Пуассона часто определяют по «правилу смесей» (правило аддитивности).
Модуль в продольном направлении
Ex = EaV*.0 + EuV*.0. (16.19)
Коэффициент Пуассона
VKa = vBVB.0 + vMVM.0( (16.20)
Где V0 — объемная доля, а нижние индексы «в» и «м» обозначают волокно и матрицу соответственно. 228

 Опубликовано в
Опубликовано в