Такие физико-механические свойства материала, как плотность, упругость, структурное строение, определяют посто­янные, характеризующие распространение в среде упругих волн, т. е. акустические свойства среды. Здесь рассматриваются изотропные среды, свойства которых оди­наковы во всех направлениях. К акустиче­ским свойствам сред относятся скорость распространения волны, коэффициент затухания и удельное волновое сопротив­ление (характеристический акустический импеданс). В твердом теле эти величины определяют для продольных и попереч­ных волн (табл. 1.3).

Скорость продольной волны в жид­костях и газах

С = у[Г/ р ,

где L - модуль всестороннего сжатия (мо­дуль всестороннего сжатия в литературе принято обозначать буквой К, но эта лите­ра очень часто используется в дальнейшем для обозначения гибкости). Скорость про­дольной волны в твердом теле, размеры которого в направлении, перпендикуляр­ном к направлению распространения вол­ны, много больше длины волны,

с = I

1 V р(1 + vX1 - 2v) ’ где Е - модуль нормальной упругости.

1.3. Акустические свойства веществ Вещество Скорость волн с, МО3 м/с Плотность р, 1-Ю3 кг/м3 Волновое сопротивле­ние Z, 106 Па с/м Коэффициент затухания на 2,5 МГц 8, Нп/м продольных поперечных Алюминий 6,36 Me т 3,13 аллы 2,7 17,2 0,1 ... 1 Бериллий 12,8 8,6 1,82 23,3 - Бронза 3,5 ... 3,8 2,3 ... 2,5 8...9 30 ... 34 - Вольфрам 5,32 2,77 19,3 102,7 - Дуралюмин 6,2... 6,4 3 ... 3,2 2,7... 2,8 19... 20 0,1 ... 1 Железо 5,92 3,23 7,8 46,3 0,2... 5 Латунь 4,3 ... 4,7 3,1 ...3,5 8,4.. .8,5 36 ...40 - Магний 5,74 3,1 1,74 9,98 0,1 ...2 Медь 4,72 2,4 8,9 42 2,5 ... 20 Никель 5,7 3,0 8,9 50,7 - Олово 3,32 1,65 7,3 24,2 - Ртуть 1,45 - 13,6 19,7 0,34 Свинец 2,16 0,87 11,4 24,6 - Серебро 3,65 1,65 10,5 38,3 - Сталь: углеродистая аустенитная 5,90 ... 5,94 5,77 ...6,14 3,22... 3,25 3,2 ... 3,31 7,7 ... 7,9 7,6 ... 8 45,9 ... 46,3 44... 48 0,1 ... 10 0,3 ... 40 Титан 6,1 3,13 4,5 27,5 - Титановые сплавы ВТ, ОТ 6,05 ... 6,3 3,1 ... 3,3 4,5 ... 4,7 27 ... 29 - Цинк 4,17 2,41 7,1 29,6 - Чугун 3,5 ... 5,6 2,2... 3,2 7,2 ... 7,6 26... 42 0,3 ... 50 Бетон 2,1 ... 5,2 Нем е т аллы 1,8 ...2,8 6... 9,5 Кварц плавленый 5,95 3,75 2,2 13,1 0,31 Полистирол 2,35 1,13 1,06 2,5 10... 13 Резина 1,4 ...2,3 - 0,9 ... 1,6 2... 3 30 ... 60 Стекло оконное 5,1 ... 6,2 3,1 ... 3,6 2,1 ... 2,6 11 ... 15 0,4... 0,7 Стекло органиче­ское 2,7 ... 2,75 1,12... 1,13 1,17...1,19 3,0... 3,3 20 ...30 Текстолит 2,4... 2,8 1,1 ... 1,4 2,3 ... 2,5 6 ... 6,4 80... 120 Фарфор 5,2 ... 6,8 3,1 ...4 2,3 ... 2,6 15 ...20 0,1 ... 0,4 Фторопласт 1,35 - 2,2 30 160 Эбонит 2,4 - 1,2 2,9 90 ЭД-5 2,3 1Д5 1,2 2,8 100

Скорость поперечной волны

]j 2p(l + v) Jp ’

где G - модуль сдвига. Таким образом, скорости объемных волн пропорциональ­ны квадратному корню из отношения мо­дуля упругости к плотности, т. е. они воз­растают с увеличением упругости среды (которая показывает величину деформа­ции при заданной нагрузке) и уменьшают­ся с увеличением плотности. Важно отме­тить, что скорость определяется физиче­скими свойствами среды и не зависит от частоты или амплитуды волн (при не­больших величинах амплитуд).

Изменение скорости с с температу­рой t определяется по формуле

c = c0+Kc(t-t0),

где с0 - скорость при исходной темпера­туре to. Температурный коэффициент скорости Кс [в м/(с-град)] у газов положи­тельный (например, у воздуха +0,6), у жидкостей отрицательный (например, у спирта -3,6), однако у воды аномальный (+2,5); у твердых тел отрицательный [для продольных и поперечных волн в метал­лах - (0,4 ... 2), у органического стекла -

3] , т. е. в твердых телах скорость уменьша­ется с повышением температуры.

Удельное волновое сопротивление среды (называемое также характеристи­ческим импедансом среды) представляет собой отношение акустического давления к колебательной скорости в бегущей волне:

z = p/v.

Для сред с большими потерями аку­стической энергии величина z имеет ком­плексный характер (см. разд. 1.4) , однако в большинстве случаев ее можно считать действительной и численно равной произ­ведению плотности р на скорость звука с:

Z - рс.

Размерность z в Па с/м.

Удельное волновое сопротивление среды в литературе (в том числе ино­странной) часто не вполне правильно на­зывают акустическим импедансом (сопро­тивлением), причем существуют два раз­личных определения последнего.

В воздушной акустике акустический импеданс определен как отношение зву­кового давления к объемной колебатель­ной скорости [317] и имеет размерность Па-с/м3. В таком понимании этот термин в нашей книге не применяется.

Акустическим импедансом называют также отношение звукового давления к колебательной скорости в наиболее общем случае, когда в системе существуют как бегущие, так и стоячие волны (в том числе резонансы). При этом акустический импе­данс зависит не только от волнового со­противления среды, но и от размеров и формы колеблющейся системы. Этой ве­личиной здесь будем пользоваться, но не­обходимо отличать ее от волнового сопро­тивления. Очевидно, что акустический импеданс имеет ту же размерность, что и удельное волновое сопротивление среды. Отметим, что в иностранной литературе акустический импеданс и волновое сопро­тивление среды выражают в рэлеях (Rayls). Это в России пока не принято.

В отличие от механического импе­данса (см. разд. 1.4) акустический импе­данс и волновое сопротивление среды яв­ляются удельными (отнесенными к еди­нице площади) величинами. В дальней­шем, там, где не возникает опасность ино­го толкования, будем пользоваться терми­ном "волновое сопротивление среды", или просто "волновое сопротивление".

Величина волнового сопротивления применяется в расчетах по прохождению и отражению волн на границах различных сред, а также по излучению и приему УЗ - волн. Волновое сопротивление определя­ется только свойствами среды в отличие от механического импеданса, который зависит от размеров, формы, материала и других параметров конструкции, в кото-

рой возбуждают колебания (см. разд. 1.4). Волновое сопротивление для изгибной волны выражается более сложным образом.

Коэффициент затухания 5 характе­ризует ослабление волны вследствие не­обратимых потерь при ее распространении в среде (см. разд. 1.1.1). Коэффициент за­тухания складывается из коэффициента поглощения и' коэффициента рассеяния'. 5 = 5П + 5р. При поглощении акустическая энергия переходит в тепловую в результа­те действия теплопроводности (отвод энергии от элементарного объема, испы­тывающего расширение и сжатие), упруго­го гистерезиса (зависимость напряжение - деформация описывается разными кривы­ми при расширении и сжатии) и вязкости (в жидкости). При рассеянии энергия ос­тается акустической, но уходит из направ- ленно-распространяющейся волны. По­скольку

e-(«n+8p> =e-8„r e-Vf

действие поглощения и рассеяния опреде­ляется двумя независимыми множителя­ми.

Изменение коэффициента затухания с температурой описывается формулой

5 = 50[l + *g(/-/0)],

где 50 - коэффициент затухания при ис­ходной температуре /0; К?, - температур­ный коэффициент затухания. Изменение коэффициента затухания с температурой обусловлено вариацией коэффициента

поглощения [27].

Для газов и большинства жидкостей, не засоренных пылью, пузырьками, рас­сеяние отсутствует, а коэффициент по­глощения пропорционален квадрату час­тоты:

5 = 5’/2.

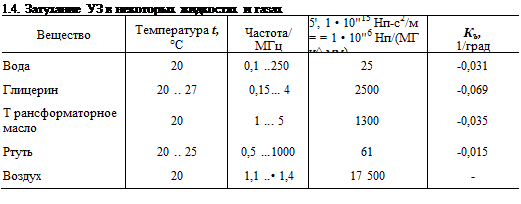
Значения 5' приведены в табл. 1.4. В ней также дан температурный коэффи­циент.

Для твердых материалов температур­ный коэффициент затухания обычно по­ложителен. Для углеродистой стали он равен ~0,04 дБ/град. Коэффициент погло­щения, как правило, пропорционален час­тоте. Коэффициент рассеяния равен нулю для аморфных тел (стекла, однородной пластмассы). Для поликристаллических веществ, в частности металлов, рассеяние увеличивается с ростом упругой анизо­тропии, которая проявляется в изменении скорости звука по разным направлениям в кристалле.

Распространяющаяся в твердом теле волна встречает на своем пути различно ориентированные кристаллы (точнее, кри­сталлиты, или зерна, - кристаллы с пра­вильной решеткой, но неправильной внешней формой). Скорость звука в со­седних кристаллах может быть разной, в результате чего возникает локальное от­ражение волны.

Чем больше упругая анизотропия в материале, тем больше рассеяние в нем УЗ. Перечислим некоторые металлы по

мере возрастания в них упругой анизотро­пии: вольфрам (упругая анизотропия от­сутствует), алюминий, альфа-титан, аль­фа-железо (углеродистая сталь), гамма - железо (нержавеющая сталь), бета-титан, медь.

Коэффициент рассеяния зависит так­же от среднего размера кристаллитов D и частоты / Например, в малоуглеродистой стали при длине волны X > 10D для про­дольных и поперечных волн

5, *0,12/ + 2(Ш3/4;

5, w 0,1 / + 105Z)3/4 ,

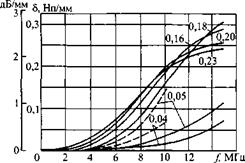
где D в мм,/ в МГц, 5 - в Нп/м. Первый член определяет поглощение, а второй - рассеяние. Отметим, что коэффициент затухания всегда возрастает с ростом час­тоты. Значения коэффициентов затухания в зависимости от частоты для низкоугле­родистой стали приведены на рис. 1.13, а для волн в жидкости и продольных волн в некоторых твердых телах на частоте

2,5 МГц - в табл. 1.3.

Рассмотрим особенности затухания УЗ-волн в железе и его сплаве с углеродом - стали [192]. Железо имеет несколько кри­сталлических модификаций, в том числе низкотемпературную альфа-железо с объ­емно-центрированной кубической кри­сталлической решеткой и высокотемпера­турную гамма-железо с гранецентриро­ванной кубической решеткой. Гамма - железо в сплаве с углеродом называют аустенитом. Как следует из приведенного выше перечня, последняя модификация имеет большее затухание.

Аллотропическое превращение одно­го типа железа в другой происходит при температуре ~1000 °С. Введением леги­рующих элементов высокотемпературную модификацию (аустенитную сталь) можно сохранить при комнатной температуре. Так получают коррозионно-стойкую сталь. Она не обладает ферромагнитными свойствами.

Как отмечалось выше, на затухание большое влияние оказывают средняя ве-

Рис. 1.13. Коэффициент затухания продольных (--- ) и поперечных (-- ) волн в низкоуглеродистом железе; указан средний размер зерна в мм

личина зерна металла и ее отношение к длине волны УЗ. Чем мельче зерно, тем лучше контролируется металл УЗ. Из­мельчение структуры и уменьшение зату­хания происходят при обработке давлени­ем (ковке, прокатке).

Для обычной углеродистой стали на основе альфа-железа измельчение зерен происходит также при термообработке типа закалки или нормализации. Металл нагреванием переводят в состояние аусте­нита, а затем быстро охлаждают. Чем бы­стрее охлаждение, тем мельче кристалли­ты (зерна) в образовавшемся альфа - железе. В гамма-железе таким образом измельчить зерна нельзя, этого можно добиться только путем обработки давле­нием.

В углеродистой стали в зернах, ос­тавшихся после зерен аустенита (первич­ных зернах), образуются более мелкие вторичные зерна (обычно в форме пла­стин) альфа-железа и цементита (химиче­ского соединения железа с углеродом). На коэффициент затухания влияют размеры как первичных, так и вторичных зерен.

Измерение скорости. Ниже рассмот­рены способы измерения скорости звука с помощью универсального УЗД или (толь­ко для продольных волн) толщиномера. Измерение скорости с помощью специ­альных приборов описано в разд. 7.1. Если дефектоскоп (например, УД2-12) содер­жит блок измерения времени пробега УЗ - импульса в микросекундах, желательно иметь образец с известным временем про­бега УЗ на определенной базе. Если в де­фектоскопе такого блока нет, то необхо­дим образец с известными толщиной и скоростью звука.

Скорость продольных волн.

1. Измерить штангенциркулем или микрометром толщину И или путь г УЗ в ОК.

2. Настроить прибор (не имеющий блока измерения времени) на правильное измерение толщины h0 образца с извест­ной толщиной и скоростью звука с0.

3. Прибором, настроенным на изме­рение скорости звука с0, измерить толщи­ну ОК г. Эта величина может отличаться от истинной толщины ОК, поскольку прибор настроен не на скорость звука в ОК.

4. Рассчитать искомую скорость зву­ка в ОК по формуле

с = г /1 = с0г / г0. (1-7)

Если прибор имеет блок измерения времени, то действия по пп. 2-4 заменя­ют на следующие:

2') настроить прибор на правильное измерение времени пробега; для этого регулировать начало отсчета времени, добиваясь правильного значения времени пробега УЗ через заданную базу, например использовать СО-2, в котором при толщи­не 59 мм время прохождения продольных волн 20 мкс;

3') измерить время пробега і УЗ через ОК;

4') рассчитать искомую скорость зву­ка в ОК: с = r/t. Если измерение выполня­ют по донному сигналу ОК толщиной h, то с = 2hit.

Для повышения точности измерения скорости звука рекомендуются такие пути:

а. Использовать для измерений ин­тервал не между зондирующим импуль­сом и донным сигналом, а между эхосиг - налами от двух отражателей, находящихся на разном расстоянии, принимаемыми при неизменном положении преобразователя, например интервал между первым и вто­рым донными сигналами. Благодаря это­му исключается погрешность от пробега УЗ в протекторе ПЭП и слое контактной жидкости.

При невозможности выполнить эту рекомендацию следует принять меры к стабилизации акустического контакта, использовать способ измерения прибором с блоком измерения времени, применять преобразователь без протектора. Если из­мерение выполняется по двум эхосигна- лам, отпадает необходимость в образце с известным временем пробега как базы для настройки прибора с блоком измерения времени. В этом случае за t принимается разность времен пробега до двух отража­телей.

б. Измерения выполнять на возможно более высокой частоте, высоту эхосигна - лов, по которым проводятся измерения, поддерживать постоянной в пределах 10 %, измерения вести по переднему фронту на одинаковой высоте (5 ... 10 мм) от линии развертки.

в. Длину базы выбирать возможно большей, например целесообразно ис­пользовать интервал между первым и третьим или четвертым донными сигнала­ми, а не между первым и вторым. Изме­рять длину базы с погрешностью < 0,1 %, шероховатость поверхности ввода должна быть не хуже Ra 2 мкм, непараллельность поверхностей не хуже 0,05.

г. Выбрать базы для ОК и образца та­кими, чтобы времена пробега в них УЗ были близкими. Это уменьшит погреш­ность от неточности глубиномера.

При соблюдении указанных реко­мендаций погрешность может быть сни­жена с 2 ... 5 до 0,5 ... 1 % при толщине ОК > 50 мм.

Пример 1.3. Измерить скорость продольных волн в пластмассе с помощью толщиномера. Оце­нить погрешность измерения.

Измерение штангенциркулем толщины ОК дало г = 5,6 мм. Поскольку толщина ОК невелика, в качестве средства измерения выбираем толщи­номер, а как образец с известной скоростью звука - стальной образец толщиной (измерена штанген­циркулем) 12,1 мм, для которого отсчет толщины (без предварительной настройки прибора) близок к отсчету для пластмассового ОК. Скорость звука

в стальном образце (измеренная лазерным спосо­бом) с0 = 5,926 мм/мкс.

Регулируя параметр "скорость" толщиноме­ра, добиваемся точного измерения толщины стального образца: 12,1 ± 0,1 мм. Измерения на ОК дали отсчет толщины г0 = 13,1 ±0,1 мм. По формуле (1.7) рассчитываем скорость звука в ОК:

с = 5,926 -5,6/13,1 = 2,53 мм/мкс.

Оценим максимальную погрешность изме­рения. Из (1.7) следует

Ас _ Ас0 + Аг Аг0 с с0 г га

Здесь учтено, что погрешность от вариации значения скорости звука в стали определяется не точностью измерения ее лазерным или другим способом, а точностью настройки толщиномера на эту скорость. Погрешность можно уменьшить увеличением толщины образца пластмассы.

Скорость поперечных волн. При на­личии прямых преобразователей попереч­ных волн можно применять способ изме­рения, описанный в предыдущем случае, но такие преобразователи в комплект де­фектоскопа обычно не входят. Рекомен­дуемый здесь способ рассчитан на исполь­зование наклонных ПЭП и дефектоскопа без блока измерения времени.

1. С помощью прямого преобразова­теля настроить дефектоскоп по образцу с известной скоростью звука с0, как в п. 2 для продольных волн.

2. Подключить к дефектоскопу два одинаковых наклонных преобразователя для излучения и приема поперечных волн с углом ввода а « 44 ... 50°.

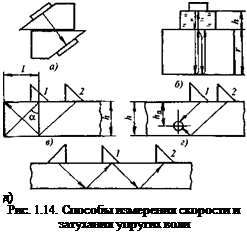
3. Смазать рабочие поверхности пре­образователей контактирующей жидко­стью (маслом) и сложить (рис. 1.14, а) таким образом, чтобы получить макси­мальную амплитуду прошедшего сигнала.

4. Измерить дефектоскопом, настро­енным на скорость звука с0, путь в приз­мах гП.

5. С помощью одного или обоих на­клонных преобразователей получить мак­симальный эхосигнал от какого-либо от­ражателя в ОК. При работе по совмещен­ной схеме это может быть отражение от двугранного угла (рис. 1.14, в) или от ци­
линдрического отверстия (рис. 1.14, г). При контроле двумя преобразователями это отражение от дна ОК (рис. 1.14, д).

Измерениями и расчетами опреде­лить путь г УЗ в ОК. Например, для схемы контроля, показанной на рис 1.14, в, по­ложению 7, преобразователя соответству­ет путь

г = л/л2 +l2 = А / cos а,

где h - глубина расположения отражателя; I - расстояние от преобразователя до от­ражателя вдоль поверхности; а - угол вво­да; / и а нужно брать для положения преобразователя, соответствующего мак­симуму эхосигнала.

6. Измерить дефектоскопом, настро­енным на скорость звука с0, путь УЗ г0 в контролируемом материале.

7. Рассчитать искомую скорость зву­ка по формуле

с = сог/(го~гП)-

При контроле прибором, имеющим блок измерения времени, используют об­разец, в котором известно время пробега УЗ, например образец с вогнутой цилинд­рической отражающей поверхностью типа CO-3, V-1 или V-2 (см. разд. 2.2.4). В по­ложении преобразователя, соответствую­щем максимуму эхосигнала, путь УЗ ра­вен удвоенному радиусу образца 27?, а

Рис. 1.1$. Дифракционное ослабление дониого сигнала

время пробега t~2Rlct. Измерения вы­полняют по пп. 2' - 4' (из измерения ско­рости продольных волн) вместо пп. 2-4. Контроль ведут одним совмещенным на­клонным преобразователем. В качестве отражателя используют двугранный угол или боковое цилиндрическое отверстие.

Погрешность измерения прибором без блока измерения времени 3 ... 5 %, а с таким блоком 1 ... 2 %. Для повышения точности измерений до 0,5 ... 1 % нужно выполнять рекомендации "а", "г" (см. вы­ше). Чтобы выполнить п. "б", желательно иметь два отражателя, которые дают эхо - сигналы при одном постоянном положе­нии преобразователя. При таком положе­нии их амплитуды могут не достигать максимума, но следует возможно более точно измерить штангенциркулем рас­стояния от точки ввода преобразователя до отражателей гх и г2, а затем определить их разность: г = г2 — п.

Пример 1.4. Измерить скорость попе­речных волн в образце из неизвестного материала толщиной А = 30 мм. Дефектоскоп имеет блок измерения времени.

Включим наклонный преобразователь иа частоту 2,5 МГц с углом ввода (для стали) 50°. Рассчитаем время пробега в СО-3 (3? = 55 мм): t = 2R/c, - 2 ■ 55/3,23 = = 34,06 мкс. Получим мак­симальный эхосигнал от СО-3. Регулируем за­держку начала отсчета времени дефектоскопа так, чтобы время пробега в СО-3 равнялось 34,1 мкс.

Получим максимальный эхосигнал от дву­гранного угла образца. Измерим дефектоскопом время t пробега в образце (например, 28,6 мкс) и штангенциркулем расстояние I (рис. 1.14, в). Пусть оно равно 33,2 мм. Рассчитаем путь УЗ в

образце: г = л/а2 + /2 = /ЗО2 +33/22 = 44,7 мм.

Импульс проходит этот путь в прямом и обратном направлениях. Скорость распространения попе­речных волн равна с, ~ 2r/t - 2 ■ 44,7/28,6 = 3,12 мм/мкс. Скорость близка к значению для алюминия.

Измерение коэффициента затуха­ння. Ослабление УЗ под действием зату­хания в материалах, обычно подвергаемых контролю, на небольших расстояниях не­велико, поэтому при измерениях коэф­фициента затухания необходимо учиты­вать поправки, также вызывающие ослаб­ление. Ниже рассмотрены способы изме­рения с применением универсального де­фектоскопа, причем учитываются поправ­ки на дифракционное ослабление и непол­ное отражение от поверхности. Измерение затухания с помощью специальных при­боров будет рассмотрено в разд. в 7.1.

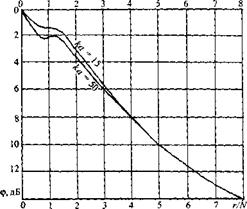
Дифракционное ослабление (ф) - это такое ослабление сигнала, которое суще­ствует при прохождении того же пути в отсутствие затухания. В дальнейшем ре­комендуется выполнять измерение зату­хания по донному сигналу ОК. В ближней и переходной зонах преобразователя ди­фракционное ослабление учитывают с помощью кривой (рис. 1.15), зависящей от приведенного расстояния: толщины ОК г, деленной на протяженность ближней зоны преобразователя (см. разд. 1.3) Л/' = а2Д,

где а - радиус пьезопластины ПЭП; К - длина волны в ОК, а также от волнового размера пьезопластины ка , где к - волно­вое число.