Применение дисперсионного анализа в задачах оценки
 4 ноября, 2011
4 ноября, 2011  admin
admin В различных оценочных процедурах довольно часто возникает потребность в осредненных показателях, которые можно было бы использовать как нормативы. Например, для приближенной оценки разнотипных машин и оборудования могут использоваться различные удельные показатели (цена на единицу массы, цена на единицу мощности и т. п.), при затратном подходе требуется средний показатель рентабельности соответствующих производств; при индексации по фактору времени нужно задаться
Средним цепным индексом; при доходном подходе требуется средняя норма амортизации и т. п.
В задачах такого рода нужно не только рассчитать интересующее нас среднее значение экономического показателя, но и доказать его устойчивость и применимость для оценки совокупности рассматриваемых объектов. В качестве инструмента служит статистический дисперсионный анализ.
Анализируемый экономический показатель рассматривается как случайная величина, которая под влиянием множества неучитываемых факторов принимает то или иное значение и для которой можно только указать закон ее распределения. Набор исходных сведений об экономическом показателе по ограниченной группе объектов рассматривают как выборку, предполагая, что существует некая генеральная совокупность. Значения экономического показателя в выборке называют точечными оценками. При этом допускают, что статистические характеристики выборки отражают с некоторым приближением статистические характеристики генеральной совокупности.
Набираемые на практике выборки однородных объектов малы по объему (обычно от 4 до 20 объектов), поэтому их называют малыми выборками. Основные статистические характеристики (статистики) малой выборки: среднее (среднее арифметическое) значение и среднеквадратическое отклонение.
Среднее значение экономического показателя в выборке:
|
|
Где Pj — Текущее значение экономического показателя у /-го объекта; П — количество объектов в выборке (объем выборки).
Среднеквадратическое (стандартное) отклонение выборки:
|
|
Процедура дисперсионного анализа включает такие этапы: 1) проверка выборки на соответствие нормальному распределе -
Нию; 2) выявление и исключение выделяющихся значений; 3) определение ошибки среднего значения и подготовка предложения по его использованию.
Проверка выборки на соответствие нормальному распределению. Эта проверка необходима для того, чтобы убедиться в статистической однородности исходных данных и обоснованно применять рассчитываемые статистические оценки в соответствии с нормальным законом распределения.
К наиболее простым методам проверки однородности данных относятся методы: предельного коэффициента вариации, среднего абсолютного отклонения и «двух сигм».
Метод предельного коэффициента вариации v заключается в его расчете по данным выборки и наложении ограничения не
Превышать 33%: v = — xl00% <33%. Если значение v превышает Р
33%, то гипотеза о нормальности распределения выборки не подтверждается.
Метод среднего абсолютного отклонения определяет условие соответствия выборки нормальному распределению в виде следующего неравенства:
![]()
Где САО — среднее абсолютное отклонение, которое рассчитывается по формуле: ![]()
Метод «двух сигм» предполагает расчет границ интервала значений экономического показателя при примерно 95%-ной доверительной вероятности:
![]()
Где/?в, Рн — верхняя и нижняя границы интервала соответственно.
Если ряд исходных данных, выстроенный в порядке возрастания экономического показателя, укладывается в границы интервала/^, ..., Рн, То считают, что выборка однородна и отвечает нормальности распределения. Если какие-то значения выпадают из
Интервала, то их рассматривают как «выбросы» и исключают далее из рассмотрения.
Так как отмеченные выше методы являются приближенными, то для уверенности в окончательном выводе целесообразно их использовать все вместе.
Выявление И Исключение выделяющихся значений. Если на предыдущем этапе обнаружены неудовлетворительные результаты проверки на нормальность распределения, то выявляют и исключают из выборки выделяющиеся значения.
Предварительно исходные данные располагают в порядке их возрастания. Выделяющиеся значения («выбросы») обнаруживаются на концах упорядоченного ряда значений. Это можно заметить даже визуально, а для наглядности можно построить гистограмму.
Явно выделяющиеся значения исключают из выборки и измененную выборку снова проверяют на нормальность. Возможно и добавление в выборку новых данных. Если условие нормальности выполнено, то затем рассчитывают показатели ошибки для среднего значения и делают вывод о возможности использования этого экономического показателя в процедуре оценки рыночной стоимости.
Рассмотрим пример. Для ускоренной оценки парка оборудования, состоящего в основном из металлорежущих токарных станков, было решено использовать такой удельный показатель, как цена станка, приходящаяся на 1 м2 занимаемой станком площади. По данным находящихся в продаже новых токарных станков была сформирована выборка и рассчитан для каждой модели станка показатель — цена станка на 1 м2 площади (табл. 4.7).
Для полученной выборки удельного показателя рассчитали основные статистические характеристики — среднее значение и среднеквадратичное отклонение, использовав функции СРЗНАЧ И СТАНДОТКЛОН В MS Excels = 105342 руб., S - 21997 руб.
Далее выполнили проверки на соответствие нормальному распределению. Коэффициент вариации v = 20,9%, что хотя и меньше 33%, но все-таки существен по величине. Проверка по критерию среднего абсолютного отклонения (САО) дала вполне удовлетворительные результаты: — 0,105 < 0,107. При его расчете была использована функция СРОТКЛ. Проверка методом «двух сигм» показала, что доверительный интервал лежит в границах от Рн = 61347 до Рв= 149337.
Таблица 4.7 Расчет удельного экономического показателя для токарных станков
|
Площадь, |
Цена стан - |
||
|
Модель станка |
Цена станка (без |
Занимаемая |
Ка на 1м2 |
|
НДС), руб. |
2 |
Площади. |
|
|
Станком, м |
Руб. |
||
|
1М63Н |
799576 |
9,26 |
86385 |
|
1М63Н-1 |
737796 |
6,59 |
112025 |
|
1М63Н-0 |
804830 |
5,16 |
155914 |
|
16К40 |
622880 |
10,75 |
57942 |
|
I6K40-1 |
792627 |
7,16 |
110687 |
|
1Н65х5 |
1998305 |
18,00 |
111042 |
|
1Н65хЗ |
1601695 |
13,51 |
118556 |
|
1К625Д |
427118 |
3,46 |
123445 |
|
16820x1500 |
368644 |
4,04 |
91249 |
|
1В62Г |
334745 |
3,33 |
100524 |
|
16В20х750 |
300847 |
3,33 |
90344 |
|
CU325x750 |
228813 |
2,07 |
110538 |
|
С U 500x1000 |
402540 |
4,07 |
98904 |
|
CU500x!500 |
436440 |
4,07 |
107233 |
Для выявления «выбросов» расположим значения удельного показателя в порядке возрастания:
57942 86385 90344 91249 98904 100524 107233 110538 110687 111042 112025 118556 123445 155914
Нетрудно заметить, что крайние значения в упорядоченном ряду выходят за границы доверительного интервала, найденного методом «двух сигм».
Для лучшей наглядности построим гистограмму (рис. 4.9).
Из рис. 4.9 хорошо видно, что значения показателя под номерами 1 и 14 выпадают из монотонной динамики, поэтому исключим их из выборки.
Для измененной выборки были рассчитаны статистические характеристики: ~р = 105077 руб., S = 11620 руб. Коэффициент вариации существенно уменьшился и составил v = 11%, что намного меньше 33%. Проверка по САО подтвердила соблюдение неравенства 0,034 < 0,107. Метод «двух сигм» позволил получить доверительный интервал в границах от Рн = 81836 до/?в = 128318, причем все значения выборки лежат в этих границах.
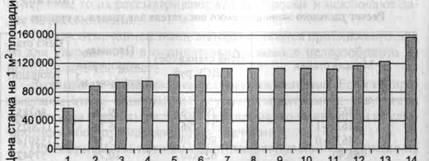
Номер значения в упорядоченном ряду Рис. 4.9. Гистограмма значений удельного показателя — цена станка на 1 м2
Таким образом, после исключения двух выделяющихся значений получили достаточно однородную выборку, отвечающую нормальному распределению.
Определение ошибки среднего значения показателя и подготовка Предложения по его использованию в задаче оценки стоимости. На данном этапе нужно решить вопрос о том, насколько надежен удельный экономический показатель и можно ли использовать его среднее значение в задаче оценки стоимости. Ответ на этот вопрос дает определение абсолютной и относительной ошибки среднего значения показателя. Эта ошибка предопределяет итоговую ошибку при оценке стоимости.
Абсолютная ошибка среднего значения экономического показателя рассчитывается по формуле
![]()
Где Tpn - критерий Стьюдента при заданной доверительной вероятности Р И объеме малой выборки П Находится либо по соответствующим таблицам в книгах по математической статистике, либо с помощью функции СТЬЮДРАСПОБР В MS Excel; S — Среднеквадратичное отклонение точечных значений малой выборки.
|
|
Относительная ошибка среднего значения экономического показателя рассчитывается по формуле:
![]()
![]() Приемлемая величина ошибки зависит от требований по точности к результатам оценки стоимости. Для условий массовой, укрупненной оценки экономический показатель может быть признан удовлетворительным, если относительная ошибка его среднего значения не превышает примерно 10%. В противном случае показатель считается неустойчивым, а его применение в оценке будет сопровождаться внесением слишком большой ошибки.
Приемлемая величина ошибки зависит от требований по точности к результатам оценки стоимости. Для условий массовой, укрупненной оценки экономический показатель может быть признан удовлетворительным, если относительная ошибка его среднего значения не превышает примерно 10%. В противном случае показатель считается неустойчивым, а его применение в оценке будет сопровождаться внесением слишком большой ошибки.
Обратимся к нашему примеру. Значение критерия Стьюдента было получено в MS Excel с помощью функции СТЬЮДРАС-ПОБР(ос = 0,05; /7—1 = 11) = 2,2. Абсолютная ошибка среднего значения экономического показателя (цены станка на 1 м2) составила 2,2x11620/V[2 ш 7383 руб. Относительная ошибка среднего значения показателя (7383/105077) х 100 = 7,03%. Значение ошибки можно признать приемлемым, и поэтому удельный показатель — цена станков на 1 м2 занимаемой ими площади — в размере 105077 руб. может быть использован для практики оценки. Нужно, однако, иметь в виду, что значение полученного показателя относится, во-первых, к станкам токарной группы и, во-вторых, к определенному времени (в данном случае к моменту, когда были зафиксированы цены, вошедшие в выборку).

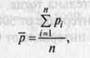
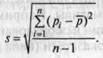
 Опубликовано в
Опубликовано в
При обработке данных эксперимента наиболее разработанными и поэтому распространенными считаются две модели. Их различие обусловлено спецификой планирования самого эксперимента. В модели дисперсионного анализа с фиксированными эффектами исследователь намеренно устанавливает строго определенные уровни изучаемого фактора. Термин «фиксированный эффект» в данном контексте имеет тот смысл, что самим исследователем фиксируется количество уровней фактора и различия между ними. При повторении эксперимента он или другой исследователь выберет те же самые уровни фактора. В модели со случайными эффектами уровни значения фактора выбираются исследователем случайно из широкого диапазона значений фактора, и при повторных экспериментах, естественно, этот диапазон будет другим.