Процесс деформирования любого материала является весьма слож­ным, особенно вблизи концентраторов напряжения. Точность описания это­го процесса зависит от сложности математической модели. Трудоемкость моделирования также зависит от сложности модели и практически не имеет верхнего предела. Однако разумная граница сложности и точности модели­рования все же существует. Во-первых, она связана с целью получения ре­зультатов расчета. Во-вторых, точность в принципе ограничена погрешно­стями исходных данных. Известно, что рассеяние всех характеристик мате­риала при современном уровне технологии может достигать 10 % как в пределах партии деталей, так и в пределах сечения одной детали. Рассеяние условий нагружения может быть еще больше.

Таким образом, при проектировании всегда приходится сталкиваться с некоторой неполнотой данных для расчета. Погрешности моделирования невозможно полностью устранить и даже оценить расчетным путем. Для их оценки необходимо сопоставление с экспериментом. Погрешности можно снизить и путем подгонки данных (решением так называемой обратной за­дачи). Ориентируясь на расчетно-экспериментальный подход, следует при выборе модели не столько стремиться к учету всех мелких деталей, сколько следить, чтобы не был пропущен принципиально важный элемент.

Наиболее универсальной и рациональной основой уравнений МКЭ является вариационное интегральное уравнение

JCyijdv = jq^dv + J p, u,ds + j'aynfids = 0, (2.4)

V V sp su

где qnPi — векторы* распределенных нагрузок, действующих в объеме мо­дели V и на части ее поверхности Sp; и — вектор нормали к той части по­верхности Su, на которой заданы граничные перемещения; с у, єі;, йі —

напряжения и скорости деформаций и перемещений в точках тела.

По своему физическому смыслу — это уравнение сохранения энергии. Скорость изменения энергии деформаций (левая часть) равна суммарной

Здесь и далее используется тензорная форма записи для векторов и матриц. Вы­ражение Pi применяется для обозначения как компонента вектора р, так и для обозначения всего вектора (р,рг, ---,Рь Р„)- Выражение означает скаляр-

п

ное произведение векторов р и q, т. е. рдг

1=1

мощности объемных и поверхностных внешних сил. Равновесие во внут­ренних и внешних точках объема V достигается путем минимизации потен­циальной энергии системы. Исходная формулировка, основанная на законе сохранения энергии, является принципиальной для моделирования движе­ния трещин, так как позволяет следить за балансом энергии в конструкции по кинетике изменения компонентов НДС в отдельных ее точках.

После подстановки в уравнение (2.4) условий связи перемещений с деформациями є - =<р(ы,.) и деформаций с напряжениями о(> = /(Ё(У) из

него может быть получена система дифференциальных уравнений равнове­сия узлов КЭ модели.

Зависимости (р и /линейны только в случае упругого деформирования гладкого образца. При больших деформациях и сложной форме детали их нелинейностью нельзя пренебречь. В этом случае и система уравнений МКЭ нелинейна. Наиболее эффективный способ ее решения итерационный, со сведением на каждой итерации к системе линейных алгебраических уравне­ний. Для получения такой системы необходимо перейти от скоростей к ко­нечным приращениям перемещений и деформаций и линеаризовать выра­жения ф и f

Согласно процедуре МКЭ, объем тела является суммой объемов эле­ментов. Выбрав в качестве неизвестных перемещения узлов, поле переме­щений в пределах элемента аппроксимируют полиномом, выражая прира­щение перемещения и деформации в произвольной точке через ее координа­ты и приращения перемещений в узловых точках AUim :

	(2.5)
-B.. AU ijnm і
(2.6)

 

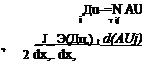где Nт — компоненты вектора функций формы элемента, зависящих от координат точки и геометрии элемента (ш — номер узла в элементе); мат­рица градиентов элемента BiJnm получается дифференцированием вектора

Nm по координатам х„. Совокупность формул (2.5) и (2.6) обеспечивает линейность функции ф. Для функции/ используют уравнение вида

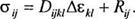(2.7)

Тогда система линейных уравнений относительно приращения узло­вых перемещений за шаг AUrt равна:

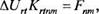(2.8)

— вектор объемных и поверхностных внешних нагрузок, включающих в себя и составляющие от неуравновешенных начальных напряжений.

Процедура расчета НДС сводится к составлению системы уравнений

(2.7) и решению ее методом Гаусса. Вначале производится факторизация матрицы Кгтт на две треугольные матрицы, а затем умножение этих мат­риц на вектор Fnm. Результатом решения являются приращения перемеще­ний в узлах AUrt, по которым могут быть найдены любые компоненты НДС. Весь процесс нагружения разбивают на шаги по времени или другому аналогичному параметру и итоговые деформации и перемещения определя­ют как сумму перемещений на отдельных шагах.

На каждом этапе составления и решения системы уравнений возни­кают погрешности, связанные как с линеаризацией, так и с ограниченной точностью выполнения математических операций на ЭВМ. Поэтому по­лучаемое решение AUrt отличается от точного значения перемещений за шаг. Если по найденным перемещениям вычислить деформации и напря­жения, а затем вновь вычислить вектор правых частей системы линейных уравнений, то компоненты этого вектора оказываются отличными от ну­ля. Повторное решение системы дает поправку к вектору AUrt. В этом заключается процедура итерационного уточнения решения, которая мо­жет быть продолжена до получения необходимой точности определения перемещений. При этом скорость сходимости итераций зависит от по­грешностей линеаризации при составлении матрицы жесткости Кг1пт и от погрешностей решения.

Предел, к которому стремятся результаты итераций, зависит практически только от правильности вычисления вектора Fnm правых частей системы, при­чем применение при вычислении правых частей выражений любой сложности не изменяет линейного характера системы (2.8). Таким образом, алгоритм сво­дится к чередованию вычисления поля перемещений, обеспечивающего совме­стность деформаций и равновесие напряжений из решения системы линейных уравнений и вычисления по этим перемещениям поля напряжений и деформа­ций в отдельных элементах с использованием при необходимости любых нели­нейных зависимостей. Независимое вычисление компонентов НДС вызывает
нарушение равновесия между элементами, которое устраняется при следую­щем решении системы (2.8). При правильном ходе итераций компоненты век­тора Fnm и поправки к решению Л Urt убывают. По их текущему значению можно судить о достигнутой точности и принимать решение о завершении ите­раций и переходе к следующему шагу изменения граничных условий.

Особенностью разработанного алгоритма является совмещение итера­ций, устраняющих погрешности округления при решении системы уравне­ний и обеспечивающих учет геометрической и физической нелинейности. Использование для вычисления вектора оправых частей напряжений, а не

их приращений АОу позволяет обеспечивать равновесие напряжений в кон­це каждого шага и автоматически корректировать погрешности в равнове­сии тела, возникающие вследствие ограниченной точности расчета. В пра­вой части системы появляются ненулевые коэффициенты Fnm, если в конце шага нарушено равновесие в узлах, независимо от того, вызвано это нару­шение изменением нагрузки, нелинейностью или погрешностями счета. Ал­горитм обеспечивает максимальную устойчивость процесса моделирования при любых видах нелинейности модели. Без учета нелинейности, в частно­сти, невозможно описание процесса разрушения материала.

Геометрическая нелинейность связана с двумя явлениями при дефор­мировании материала, не учитываемыми линейной формулой (2.6). Во - первых, возможно вращение объема, окружающего точку, в которой произ­водится определение деформаций, как жесткого целого относительно задан­ной системы координат. При этом материал не деформируется, но взаимные перемещения соседних точек происходят, и выражение (2.6) дает ненулевые компоненты деформаций. Если отрезок АВ, направленный вначале вдоль оси х, поворачивается вокруг точки А без изменения длины АВ, то, согласно (2.6), деформация гхх отрезка отрицательна. Фактически (2.6) дает дефор­мацию не самого отрезка АВ, а его проекции на ось х. При моделировании возникновение деформаций и напряжений в жестко вращающейся части вы­зывает изменение энергии и появление реакций, препятствующих враще­нию, в то время как в реальности вращение жесткого тела в пространстве при отсутствии внешних сил происходит беспрепятственно. Чтобы исклю­чить эту погрешность, искажающую картину НДС, необходимо воспользо­ваться более точной формулой для определения деформации

д(А»,-) , д(Дц/) ( д(Аик) д(Аик) дх. дх. дх{ дх/

Сравнение выражений (2.6) и (2.11) показывает, что различие между ними остается в общем случае существенным, даже если шаг решения стре­мится к нулю.

Вторая причина геометрической нелинейности связана с изменением базы деформации при значительных перемещениях за шаг. Поскольку коор­динаты концов отрезка АВ являются функциями перемещений, скорость де­формации отрезка переменна при постоянной скорости взаимного переме­щения его концов. Если пользоваться условной деформацией, т. е. за сред­нюю скорость принять скорость деформации в начале шага, то погрешность будет иметь разный знак в зависимости от того, увеличивается база дефор­мации АВ или уменьшается. В этом случае, как и в предыдущем, важен не сам факт погрешности, которая неизбежна при применении дискретного ме­тода решения, а ее влияние на моделирование НДС. Известно, что реальные металлы практически несжимаемы, их объемные деформации, особенно в пластической области, малы по сравнению с деформациями формоизмене­ния. Достигнуть условной деформации -100 %, при которой длина образца станет равной нулю, невозможно, для этого нужно совершить бесконечно большую работу. Если же не учитывать изменения базы при деформации, то эта работа окажется такой же, как при условной деформации +100 %, т. е. при увеличении исходной длины образца вдвое. Если в модели имеются зо­ны как растяжения, так и сжатия, то минимуму суммарной потенциальной энергии может соответствовать состояние с деформациями сжатия более 100 %, что означает отрицательный объем, т. е. вывернутый наизнанку. Следовательно, при деформации за шаг, соизмеримой со 100 %, в отдельных зонах возможно нарушение условия неразрывности материала модели, за­трудняющее продолжение моделирования.

Эту проблему можно решить без измельчения шага решения, если оп­ределять приращение деформаций интегрированием. Для случая линейной деформации отрезка с исходной длиной АВ, изменившего при деформации свою длину на А АВ, имеем условную деформацию

Д АВ

Деу =-------------

АВ

и истинную деформацию

Различие между условными и истинными деформациями существует и для компонентов сдвига, но формулы в этом случае гораздо сложнее. По­этому' для определения компонентов тензора Де"с проще перейти к главным осям деформаций.

Алгоритм определения истинных деформаций включает следующие операции.

1. Определение приращений компонентов перемещения узлов модели за шаг. Для этого осуществляется решение системы уравнений (2.8), постро­енной на линейных соотношениях между скоростями перемещений, скоро­стями деформаций и напряжениями, соответствующими началу шага.

2. Определение приращений компонентов тензора условных деформа­ций за шаг с учетом вращения, т. е. по формулам (2.11).

3. Выделение из приращений деформаций девиаторной части

Де,-Д8--б, Лєт) (2.14)

— средняя деформация; Ъу — символ Кронекера.

4. Определение приращений главных компонентов девиатора услов­ных деформаций Де из решения уравнения

£>е1(Де..-8,;Де) = 0. (2.15)

5. Определение матрицы направляющих косинусов nki между осями ис­ходной системы координат и главными осями из решения системы уравнений

(Де, у -8..Де, К =0, (2.16)

"и+и*22 + ин=1- (2-17)

6. Определение приращений главных компонентов тензора истинной деформации за шаг. Для этого необходимо найти приращения главных ком­понентов тензора условных деформаций Дє|с = Aek + Дєт и затем опреде­лить Дг™ по (2.13).

7. Определение приращений компонентов истинной деформации в ис­ходной системе координат. Для этого надо воспользоваться найденными направляющими косинусами

Дє^Дє^Ид. (2.18)

Как уже было отмечено, описанный алгоритм нацелен не столько на повышение точности решения, сколько на обеспечение разумного поведе­ния модели в условиях огромных шагов приращения деформаций в отдель­ных элементах. Таких мер может быть достаточно, только если состояние в этих элементах не представляет интереса (например, это зона уже разру­шившегося материала), а требуется точно оценить состояние в соседних элементах с меньшими поворотами и деформациями за шаг. Для обеспече­ния точности всей модели необходимо ограничивать шаги решения, а также учитывать изменение матрицы градиентов BiJnm при вычислении по (2.8)

правых частей системы уравнений на каждой итерации.

8. Существенные погрешности могут возникнуть при переходе к сле­дующему шагу решения. Описанная выше процедура исключает влияние поворотов на НДС в точках модели. Это значит, что элементарный объем, имевший в начале шага напряжение стхх - а, суу = 0 и повернувшийся за

шаг как жесткое тело на 90° вокруг оси z, будет иметь то же напряжение. Но фактически волокно, совпадавшее в начале шага с осью х, в конце шага по­вернулось в направлении оси у, следовательно, в неподвижной системе ко­ординат НДС в этом объеме соответствует ст^ = 0, ауу = а. Таким образом,

при переходе к следующему шагу одновременно с изменением координат точек модели в результате их перемещений необходимо преобразовать НДС.

Эта задача распадается на две. Во-первых, необходимо определить, как повернулся каждый элементарный объем, т. е. найти направляющие ко­синусы между осями координат и теми волокнами, которые совпадали с этими осями в начале шага. Направляющие косинусы любого волокна t в конце шага

m, i = (ийф. - i7„.cpA)sin Лео + ф, б(1 - cos Лео) + па cosAco, (2.19)

л ЛСО,

где о = ; ф: =—L; па — направляющие косинусы того же волокна в

Лю

начале шага. Три угла поворота элементарного объема за шаг Дюг опреде­ляем по формулам

d(Auk) d(Auj)

Определив девять направляющих косинусов поворота системы коор­динат, можно найти начальные компоненты НДС следующего шага по ко­нечным предыдущего, с учетом этого поворота

Столь подробное изложение процедуры учета геометрической нели­нейности связано с тем, что в литературе не удалось найти достаточно пол­ного описания, доведенного до эффективного и практически реализуемого алгоритма. Существует также представление, что для моделирования МКЭ геометрической нелинейности вполне достаточно вести расчет мелкими ша­
гами и корректировать координаты узлов после каждого шага. В действи­тельности это так, но в некоторых случаях потребуется столько шагов, что реализация решения задачи станет нереальной.

Вопросы нелинейности деформационной характеристики в литературе освещены более подробно. При анализе упругопластического поведения материала применяются две основные теории: деформационная и теория течения. Поскольку процесс нагружения при эксплуатации, а особенно при изготовлении сварных соединений, нельзя считать простым, целесообразно использовать модель материала, основанную на теории течения. Недостат­ком теории течения является ограничение на размер шага. Погрешность при замене в формулах теории течения скоростей деформаций конечными при­ращениями невелика, если эти приращения не превышают нескольких процен­тов от деформации предела текучести єт, т. е. имеют порядок до 1(Г4. Далее погрешность резко возрастает. При деформации за шаг 2єт и более решение по теории течения становится более грубым, чем по деформационной теории.

Предположение о линейности траектории деформаций в пределах ша­га позволяет аналитически проинтегрировать уравнения теории течения, ослабив тем самым ограничения на размер шага, что приводит к существен­ному сокращению вычислительных затрат. В результате интегрирования

получаем выражение напряжений в конце шага о* через напряжения в на­чале шага о“ и приращение деформации за шаг. Тензор напряжений С* состоит из девиатора S* и шарового тензора Siya^, т. е.

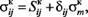(2.23)

где среднее напряжение определяется из выражения

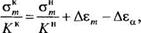(2.24)

а девиатор в конце упругого шага — из выражения

и в конце упругопластического шага — из выражения

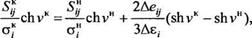(2.26)

где a*, GK, Кк — интенсивность напряжения и модуль упругости в конце шага, a a", G", К" — то же в начале шага; Деі;, Дєт, Де,, Деа — прираще­ния девиатора и шарового тензора деформации, интенсивности деформации и свободной температурной деформации за шаг.

Параметр vK определяется из выражения

среднее значение отношения — за шаг;

О;

(2.28)

Уравнения (2.23)—(2.28) могут быть применены как для идеального упругопластического материала, так и для материала с упрочнением. В пер­вом случае в конце упругопластического шага интенсивность напряжения а)' известна и равна пределу текучести а*. Во втором а* определяется из решения нелинейного алгебраического уравнения, в которое входит закон упрочнения. Этот алгоритм эффективнее численного интегрирования урав­нений теории течения, когда необходимое число шагов интегрирования больше двух.

При переменной температуре модули упругости G и К переменны. Это изменение, как видно из (2.24), (2.26), влияет на Свободная темпе­ратурная деформация, а также изменение объема от структурных превраще­ний Дест входят в Деа :

Деа = jadT + Дєст,

Л Т

где а — коэффициент линейного расширения материала, зависящий от тем­пературы.

Таким образом, приведенные уравнения выражают достаточно уни­версальную модель поведения изотропного материала, описывающую в ча­стных случаях:

• упругий материал при постоянной и переменной температуре;

• идеальный упругопластический материал при постоянной и пере­менной температуре;

• упругопластический материал с произвольным законом упрочнения при постоянной и переменной температуре.

Последний из перечисленных случаев может быть распространен и на вязкоупругопластический материал, что позволяет проводить расчеты НДС с учетом ползучести. Для этого необходимо вводить в расчет свойства мате­риала в виде изохронных кривых, т. е. зависимостей О; (є, ) в каждый мо­мент времени.

В целом модель позволяет описать с достаточной для практических целей точностью большинство деформационных процессов в металле при изготовлении и эксплуатации сварных конструкций.

Поскольку речь идет о практическом применении при проектирова­нии, необходимо обеспечение устойчивости и сходимости процесса модели­рования. Существует несколько видов задач, при решении которых сходи­мость является серьезной проблемой.

1. Модели с большим числом элементов. В этом случае причиной ите­раций является накопление погрешностей при решении системы равнений по методу Гаусса. Обычно эти проблемы возникают при десятках тысяч не­известных, однако этот порог резко снижается, если жесткость модели су­щественно различается при разных направлениях перемещений, например при моделировании стержневых и листовых конструкций. Как правило, это приводит не к увеличению числа итераций, а к полному нарушению реше­ния. Решению этой проблемы способствует переход на решение с двойной точностью, а также алгоритм обращения матрицы с добавлением к диаго­нальным элементам некоторого числа. Как правило, количество итераций при этом увеличивается, но решение становится возможным. Более карди­нальными средствами являются переход к решению в несколько этапов на основе применения суперэлементов или метода поэтапного расчета.

2. Нелинейные задачи. Хотя жесткость модели непрерывно изменяет­ся, наиболее эффективным остается метод упругих решений с постоянной матрицей Krtnm. При этом число итераций можно многократно сократить, если при вычислении вектора AUrl после очередной итерации использовать результаты предыдущих итераций. Алгоритм такого ускорения основан на определении суммарного перемещения ДUrl в виде линейной комбинации приращений перемещений на итерациях:

Аи^-^с'Чи", {230)

1=1

причем коэффициенты с0) определяются из условия минимума квадратич­ной нормы ожидаемого приращения перемещений на следующей итерации:

|б^,min) + |][с(,) -1][8[/^ - 8 и',Г)]|[8U):? - 8U^m)] = 0 . (2.31)

В общем случае получаем систему из п -1 линейных уравнений отно­сительно /7-І неизвестных коэффициентов с(,), при этом принимается с(™п) =1. Число решаемых уравнений может быть уменьшено. В этом слу­чае часть коэффициентов с(,) принимается равными единице и алгоритм становится более простым, но менее эффективным.

Эффективность применения алгоритма зависит от конкретной задачи. Обычно число итераций сокращается в 5—-10 раз.

3. Нарушение устойчивости решения. Если жесткость матрицы системы уравнений меньше, чем модели, то сходимость становится немонотонной. Если хотя бы в одной точке модели эта погрешность матрицы превышает 200 %, то приращения за следующую итерацию становятся больше, чем за предыдущую, т. е. нарушается устойчивость решения и итерации расходятся.

В зависимости от причины такого поведения модели можно предло­жить конкретные меры обеспечения устойчивости.

1. Увеличение. модуля упругости материала при изменении темпера­туры ши структурных превращениях. В этом случае необходимо пересчи­тывать матрицу К гШт на каждом шаге или рассчитать ее для максимально возможных значений модулей упругости.

2. Геометрическая нелинейность, в том числе связанная с моделиро­ванием разрушения. В тех точках, где происходит укорочение, истинные деформации по абсолютному значению больше условных, что эквивалентно увеличению жесткости модели и ведет к нарушению сходимости. Когда ус­ловные деформации укорочения приближаются к 100 %, жесткость стремит­ся к бесконечности, в связи с чем необходимо ограничивать шаги решения. Искусственно завышая модули упругости при вычислении упругой матри­цы, можно повысить устойчивость решения, что позволит несколько увели­чить шаг. Поскольку деформации сдвига вызывают текучесть и резкое сни­жение жесткости, завышение необходимо только для объемного модуля уп­ругости. Во сколько раз будет увеличен объемный модуль, во столько же раз можно допустить превышение истинных деформаций над условными без нарушения устойчивости решения.

3. Ускорение сходимости также может нарушать устойчивость решения. В результате этого возможно увеличение числа итераций, поэтому

необходимо, во-первых, ограничивать значения коэффициентов с(,) (на прак­тике ограничивали коэффициенты ускорения от -0,5 до +20) и, во-вторых, прекращать попытки ускорения, если приращения перемещений начинают увеличиваться от итерации к итерации.