Содержание цемента в бетонной смеси определяется многими факторами, к числу которых в первую очередь относятся: строение и водопоглощение заполнителя, плотность коагуляционной структуры цементного геля и наличие в нем различных добавок.

Формулу для расчета массы цемента в бетонной сме­си с учетом перечисленных факторов можно получить из равенства объема пустот между зернами заполнителя тс. б по формуле (17.3) за вычетом количества адсорби­рованной на них воды — Вад и контракционного объема цементного геля (1.18), т. е. m 0,0000ШС

1 + 0,000013^; - ^ад = Д [1 /Ря + *„, <* - *)]•

Отсюда находим расход цемента — Д, кг/м3: mc + 0,00001*/e X

Ч 1 + 0,000013^------------- ^---------- в (7Л1)

— + КЯ. АХ-Ь) Ри

Где Ь — в зависимости от параметров механического воздействия при уплотнении цементного геля колеблется между 0,292 и 0,396.

Из (7.11) следует, что расход цемента определяется не всем количеством воды в бетонной смеси, а только тем, которое содержится в цементном геле и адсорбиро­вано на поверхности зерен заполнителя. В общем случае расход цемента зависит от плотности упаковки, сум­марной поверхности зерен заполнителя и плотности ко­агуляционной структуры цементного геля.

Анализируя выражение (7.11), можно отметить, что при данном строении и адсорбционном водопоглощении заполнителей расход цемента увеличивается вместе с плотностью структуры цементного геля, а при X— const количество цемента повышается с уменьшением круп­ности зерен заполнителя (особенно песка) и /Сн. г. В ука­занных случаях без существенных изменений физико - механических свойств бетонной смесн и бетона расход цемента можно снизить, вводя в него пластифицирую­щие добавки. Экспериментально определено, что СДБв количестве 0,2% массы цемента снижает значение /Сн. гИ Рж на 10%.

Если числитель формулы (7.11) обозначить через Со, тогда при рИ=2,48 г/см3, (В/Д)г=0,4 и J=L,34 рас­ход цемента на 1 м3 непластифицированной бетонной смеси будет равен:

1/2,48 + 0,3(1,34-^0,292) ^ МС°*

При введении в бетонную смесь СДБ на таком же це­менте, но с измененными параметрами: /Сн. г=0,27; рж=1,35 г/см3, расход его по формуле (7.11) определит­ся при Х=1,48:

71 __ ________________________________ _ 1

42 1/2,48 + 0,27 (1,48 — 0,226) '

Следовательно, при добавке СДБ количество цемен­та в бетонной смеси может быть снижено на 4,5%, что согласуется со многими экспериментальными данными, опубликованными в специальной литературе.

При определении расхода цемента в легких бетонах на заполнит елях, содержащих пылевидные фракции, в формулу (7.11) следует подставлять вместо /Сн. г его значения, учитывающие влияние микрочастиц на адсор­бционную способность вяжущего. Микрочастицы, вве­денные в бетонную смесь вместе с песком, увеличивают контракционный объем цементного геля и снижают рас­ход цемента.

Микрочастицы различных каменных пород, а также трепела, диатомита, трасса и др. характеризуются вы­сокой адсорбционной способностью. В связи с этим при одинаковом строении заполнителя и (В/Ц)т расход пуц - цоланового портландцемента будет меньше, чем порт­ландцемента. В этом легко убедиться, если подставить в формулу (7.11) соответствующие значения рн и Ких для этих цементов.

Расход цемента и плотность коагуляционной струк­туры цементного геля существенно влияют на техноло­гические свойства бетонной смеси и в первую очередь на ее пластичность (подвижность). Цементный гель при­дает зернам заполнителя взаимную подвижность, кото­рая в свою очередь зависит от структурной прочности цементного геля и его количества в бетонной смеси. Чем толще слой цементного геля, обволакивающий зерна за­полнителя, тем подвижнее (пластичнее) при прочих рав­ных условиях бетонная смесь. С другой стороны, чем выше {ВЩ)Г или X, тем подвижнее окажется бетонная смесь.

Относительную подвижность бетонной смеси на про­тяжении многих десятилетий принято определять экспе­риментальным путем по осадке нормального конуса — О. К. б. Метод этот прост и удобен; он применяется как в заводских условиях, так и непосредственно на строи­тельных площадках. Вместе с тем при пользовании ме­тодом конуса требуются большой производственный опыт и развитая интуиция, так как, во-первых, нет пря­мой связи между величиной осадки конуса и формуемо - стью бетонной смеси и, во-вторых, по осадке конуса весьма затруднительно вносить поправки в состав бе­тонной смеси, не допустив при этом ошибок.

- Для раскрытия аналитической взаимосвязи между параметрами, предопределяющими величину осадки нор­мального конуса, впервые в работе [4] приведена такая зависимость, в основу которой была положена формула (3.74), полученная для цементного геля.

Значительная концентрация щебня (гравия) и песка искажает показания нормального конуса, так как при механическом зацеплении зерен крупного заполнителя (в местах их контактов) создается жесткий скелет, пре­пятствующий пластической деформации цементного ге­ля. Учитывая сказанное, минимальную осадку конуса бетонной смеси можно представить зависимостью:

ТТ VV __ А 07с

О. к.Б = 20/з ——S---------- . Тб Уг. б —ТГ^Т-------- . (7Л2>

У п+ ^щ(гр) 0,774

Где у б — объемная масса бетонной смеси, кг/м3; VQ—объем цемент­ного геля в бетонной смеси, м3; /в — коэффициент, зависящий от ше­роховатости зерен заполнителя: для гравия и окатанного песка /3= 1; для щебня, дробленого и горного песка плотных каменных пород 3 /Ц

/з = 0,9; Х'=Х~]—— (вода, адсорбированная на зернах заполни - Кн. г

Теля, пополняет количество жидкой фазы цементного геля).

Размерность О. К-б (г-см или кг-см), и на этом ос­новании можем заключить, что величина осадки нор­мального конуса определяется работой, которую надо затратить, чтобы произошла пластическая деформация объема бетонной смеси под влиянием ее собственной массы.

Анализ зависимости (7.12) показывает, что при дан­ном X' осадка конуса тем больше, чем больше песка содержится в бетонной смеси. При наиболее компакт­ном пространственном взаиморасположении зерен за­полнителя, т. е. Уп+Ущ~1 м3, независимо от состава бе­тона осадка конуса получается практически одинаковой, равной 0—1 см. Такие бетонные смеси можно формаль­но отнести к категории жестких, между тем как теку­честь их при вибрационной укладке далеко не одинако­ва, поэтому понятие о жесткости бетонной смеси без до­полнительного критерия не дает правильного представ­ления о текучести смеси.

В связи с этим необходимо внести ясность в термин «водоцементное отношение», как это предложено в рабо­те [4].

Такая интерпретация ВЩ бетонной смеси вносит яс­ность во многие технологические вопросы. Если содер­жание воды Вб в бетонной смеси строго регламентиру­ется следующей суммой: В^ = Вг-{-В^л--В110г = Вг-{-В3, то оба составляющих ее позволяют судить как о плотно­сти коагуляционной структуры цементного геля, так и о физических свойствах использованных заполнителей. Отсюда можно заключить, что дополнительными харак­теристиками пластичности бетонной смеси могут слу­жить (В/Ц)г, Кн. г и параметры, определяющие строение заполнителя, т. е.: Uc и тс.

В этой связи представляют интерес результаты ис­следований [113], которыми определено, что суммарная поверхность смеси заполнителей Uc оказывает при про­чих равных условиях основное влияние на текучесть (формуемость) бетонной смеси и прочность бетона. В ос­нове этого вывода лежит следующая предпосылка: если зерновой состав заполнителей изменять так, чтобы его суммарная поверхность оставалась величиной постоян­ной, тогда «текучесть» (пластическая подвижность) бе­тонной смеси и прочность бетона могут при прочих рав­ных условиях практически сохраняться неизменными. В самом деле, зависимость пластической подвижности бетонной смеси от Uc обусловливается тем, что при Uc= const и Х= const отношения Уп/Уп+Ущ(гр) И у б мо­гут колебаться в узких пределах, а поэтому величина О. К. б будет в основном предопределяться адсорбцион­ным водопоглощением заполнителей. Поскольку 5ад зави-

Х'—0,876

Сит от суммарной поверхности заполнителей, то —^ ^ =

= const и (J5/Z()6=const (считаем, что - бдог для запол­нителей плотных каменных пород изменяется в весьма узких пределах) и, согласно (7.12), О. K.6=const.

Сказанное выше может быть сформулировано так: при заполнении цементным гелем пустот между зерна­ми щебня (гравия) и песка и одинаковой их относи­тельной раздвижке пластическая подвижность бетонной смеси, оцениваемая по осадке нормального конуса О. К-б, может оставаться неизменной, если при данном значении /Сн. г Х=Const.

Результаты исследований [ИЗ] показали, что на од­них и тех же материалах (цементе и заполнителе), но при разных расходах цемента, бетонная смесь одной и той же пластической подвижности содержит одинаковое количество воды. Это свидетельствует о том, что изме­нение в некоторых пределах пустотности заполнителей и плотности структуры цементного геля не сказывается на изменении расхода воды и пластической подвижно­сти бетонной смеси.

Согласно зависимостям (7.11) и (7.12), количество воды в бетонной смеси может быть изменено при соот-

TA БЛИЦА 7.1. ИЗМЕНЕНИЕ ПАРАМЕТРОВ X И Ц ПРИ Br«const

		Ц			Xi	^г. б (2>
Vr.& Л	X	ВГ	Je	Хг	^г. б <!>	Ц1
164 182	1,50 1,20	209 262	94 94	0,81 0,42	1,25	1,105	1,26
162 190	1,65 1,27	204 265	101 101	1 0,51	1,30	1,13	1,30
210 234	1,65 1,27	254 328	135 125	1 0,51	1,30	1,10	1,29
220 276	1,65 1	265 435	131 131	1 0,16	1,65	1,25	1,65

Ветствующих значениях X и объемах цементного геля, т. е. расходах цемента. Пользуясь данными табл. 7.1, определим пределы изменения X и Д, при которых мо­жет соблюдаться условие Вт=const.

Из табл. 7.1 можно сделать вывод, что постоянство расхода воды при неизменной пластической подвижно­сти бетонной смеси, т. е. величине О. К.б определяется условием

(7 -13)

Это условие может быть получено следующим пу­тем:

(В/Ц), Кн. г _ (В/Ц)2Кп. т Х2 '

X II

Поскольку Вг=Const, будем иметь —- =

Х2 Цх

Вязкопластические свойства присущи цементному ге­лю при значениях X от 1 до 1,65; следовательно, Х — = 1,65 и Х2=1. На этом основании из соотношения (7.13) получаем

1(2=1,65^.

Если принять, что Z/i=260 кг/м3, то в таком случае Ц2= 1,65X260=430 кг/м3. В экспериментах максималь­ный расход составлял 423 кг/м3, что удовлетворительно согласуется с расчетной величиной Дг-

Приведенным подтверждается, что расход цемента определяется не только количеством воды в цементном геле, но и объемом его в бетонной смеси. При этом чем меньше воды в цементном геле, тем больше его должно содержаться в бетонной смеси для сохранения заданной пластической подвижности.

Таким образом, можно считать установленным, что правило о постоянстве количества воды при неизменной пластической подвижности бетонной смеси* справедли­во, если соблюдается указанная выше обратная пропор­циональность между водоцементным отношением и рас­ходом цемента.

В соответствии с этим правилом абсолютное количе­ство воды при неизменной пластической подвижности бетонной смеси должно возрасти вместе с увеличением адсорбционной способности заполнителя и цемента. При постоянном значении X и данной адсорбционной способ­ности цемента для получения определенной пластичес­кой подвижности бетонной смеси на щебне надо больше воды и цемента, чем для смеси на гравии; на пористых заполнителях водопотребность бетонной смеси и расход цемента выше, чем на щебне из плотных каменных по­род. Для достижения одинаковой пластической подвиж­ности бетонную смесь на крупном песке надо затворять меньшим количеством воды, нежели при использовании в такой же массе мелкого песка.

По величине осадки нормального конуса не всегда удается правильно оценивать формуемость и уплотняе - мость бетонной смеси, так как при определении этих свойств не учитываются тиксотропные превращения це­ментного геля, проявляющиеся в различной степени при механических (главным образом вибрационных) воздей­ствиях.

Для оценки формуемости и уплотняемости бетонной смеси под влиянием вибрации используют вибровиско­зиметр и эти свойства характеризуются временем исте­чения бетонной смеси из одной емкости в другую.

Рассматривая истечение бетонной смеси из запол­ненного отверстия в техническом вибровискозиметре (рис. 7.3, а) как установивший процесс и учитывая за­висимость (4.27), по аналогии с [122], можно записать:

=- К* ~ HI) (76 - 2т0)], (7.14)

Dt Vm

Где H — переменная высота столба смеси во внутреннем цилиндре; Hi — переменная высота столба смеси в наружном цилиндре; KK — Константа технического вискозиметра; T — время истечения; Im — условная вязкость бетонной смеси, П.

Для соблюдения условия о неизменности геометри­ческой характеристики технического вискозиметра необ­ходимо, чтобы зазор между нижней кромкой внутренне­го цилиндра и днищем прибора оставался постоянным, т. е. h=H—h, тогда (7.14) получит вид:

Dh 1

-ЗГ —~ № - яв) (Ye ~ 2т.)]. (7.15)

Dt ftn

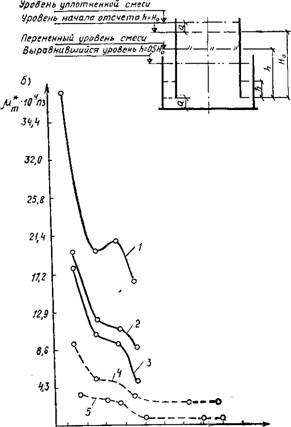
/, 2 и 3-при 0,41 и ав=0,24; 0,32 и 0,37 мм; 4 и 5-при (В/Ц)**4 =

= 0,54 и ав=0,17 и 0,37 мм

Интегрируя в пределах, в которых может изменять­ся напор, т. е. от Я0 до Яь получим

T ^ Нх

Г dt=__ Tin Г Dh

А)

50 67 63,5 ЮО МЬрГЦ Рис. 7.3. Схема вибровискозиметра (а) и пластическая вязкость бе­тонной смеси (б)

J ^K(Y6—2T0)J 2h — HQ (7,l6)

Отсюда

1д

(?б — 2т0) 2 Hi — H9

Если по условию опыта Яi=0,8 Я0, то время исте­чения будет равно

♦

* = °'256 , n V • (7.17)

MY6-2т0)

Из зависимости (7.17) следует, что время истечения T бетонной смеси из одной емкости в другую до дости­жения ею заданного уровня Л=0,5 Я0 (см. рис. 7.3, а) зависит от реологических параметров цементного геля и константы прибора. Величина kK характеризуется фор­мой и размером отверстия (через которое происходит истечение бетонной смеси), изменением площади сече­ния потока и его расхода при неустановившемся режи­ме течения и другими побочными факторами.

В зависимости от величины " ^ и то время T может изменяться от оо, когда у 6^2 т0, до нескольких секунд при то=0. Для этого случая выражение (7.17) прини­мает вид, соответствующий системе с одним реологичес­ким параметром, — пластической вязкости х,*т [ 122], а именно

'-Tibr- (7Л8)

Технический вискозиметр предназначен в основном для оценки формуемости «жестких» бетонных смесей, приобретающих свойство текучести только в процессе тиксотропных превращений цементного геля. Поэтому T — это время, в течение которого при данных динамиче­ских параметрах вибрации величины £п и т0 уменьша­ются до таких минимальных значений, при которых бе­тонная смесь достигает в сообщающихся емкостях за­данного уровня, а в цементном геле устанавливается новое устойчивое энергетическое равновесие сил взаимо­действия между структурными элементами.

Эти явления будут происходить в полной мере при резонансном совпадении частоты вынужденных колеба­ний (частоты колебаний вибратора) с собственными ча­стотами колебаний сольватированных цементных частиц. При резонансном режиме оценки формуемости бетонной
смеси время T может быть определено по зависимости (7.18), При этом под величиной £п будет подразумевать­ся некоторый условный реологический параметр, кото­рый косвенно учитывает влияние т0.

На основе такого предположения в работе [122] при­ведены результаты экспериментов по определению ус­ловной вязкости i*m бетонных смесей двух составов при различных частотах и амплитудах колебаний вибрато­ра. Для ускорения процесса истечения (уменьшения влияния структурной прочности цементного геля т0) применяли пригруз интенсивностью 0,0018 МПа.

На кривых /, 2 и 3 изменения пластичной вязкости бетонной смеси с (В/Ц)6=0,41 (см. рис. 7.3,6) имеют­ся сингулярные точки, которые независимо от значений амплитуды колебаний возникают при одинаковых час­тотах вынужденных колебаний 67—70 Гц. На кривых А и 5, соответствующих составу с (В/Ц) 6=0,54, эти ха­рактерные точки практически не обнаруживаются из-за малой структурной прочности цементного геля в этом случае. В обоих составах были использованы одинако­вые материалы, с той лишь разницей, что во втором со­ставе содержалось на 69 кг меньше гравия и песка и больше цементного геля за счет увеличенного на 46 л содержания воды. В результате перерасчета определе­но, что в первом составе а во втором Х«1,55, По формуле (2.64) и табл. 2.2 нетрудно установить, что при Х&1У1 в цементном геле при указ-анной частоте вы­нужденных колебаний возникают резонансные явления, способствующие тиксотропному его разжижению, а при Х«1,55 резонансное совпадение частот собственных ко­лебаний с вынужденными улавливается слабо.

Взаимосвязь между пластической подвижностью бе­тонной смеси, определенной по осадке нормального ко­нуса, и пластической (технической) вязкостью, измерен­ной при помощи технического вискозиметра, видна из рис. 7.4. Эти экспериментальные данные показывают, что оба параметра, косвенно характеризующие формуе - мость бетонной смеси, зависят при данном составе за­полнителей от количества воды, содержащейся в ней, или точнее от структурной прочности цементного геля.

305

В свете изложенного необходимо отметить, что при X=0,876 бетонная смесь состоит из отдельных, не связанных между собой комочков и зерен заполнителя,

20—634

Покрытых упругими оболоч­ками из цементного геля. Такая бетонная смесь не проявляет вязкопластичес - кие свойства и формуемость ее не зависит ни от состава, ни от вида заполнителя, по­скольку она представляет «юбой сыпучую (землисто - влажную) массу.

При вибрировании, на­пример с частотой 50 Гц, комочки приходят во вра­щательное движение. Стал­киваясь друг с другом, они подпрыгивают и поэтому затрудняют уплотнение бе­тонной смеси. Особенно сильно разрыхляется по­верхностный слой из-за от­сутствия пригруза лежащего выше слоя. Для соедине­ния разрозненных комков необходимо пригрузить сво­бодную поверхность бетоной смеси с тем, чтобы сбли­зить и прижать комки друг к другу до полного их сли­пания под действием вибрации.

Такая бетонная смесь сравнительно легко высыпает­ся из бункеров и распределяется в форме при встряхи­вании (вибрировании). Поэтому определяющим показа­телем жесткой (землисто-влажной) бетонной смеси яв­ляется не формуемость, а уплотняемость, под которой следует подразумевать ее способность сжиматься под влиянием собственной массы и механического воздейст­вия.

Чтобы судить о формуемости бетонных смесей, ме­тоды ее оценки должны соответствовать условиям фор­мования (бетонирования) изделий и конструкций.