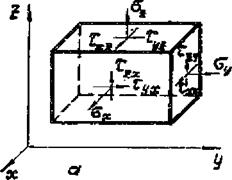
Из курсе мСопротивление материалов” известно, что пряженное состояние в радой точке тела характеризуется шестью компонентами напряжения, нормальніш 6^ ,б^,б2 и ка- стальнаш Гщ, г, х гх С рис. ?. I»а). Согласно закону пар­

ности касательных напряжений

^ху г^Х ^ 1гЕ, Х тхг. ■

Общий случай напряженного состояния можно представить в виде суша даре состояний:

1) все нормальные напряжения равны среднему напряжению (гидростатическому давлению)

і (7.2)

2) напряженая равны компонентам девиатора напряжения

^к._0о і і і ^ Х'у і 5 ^дх. - (7.3)

Как показывают опыты» в первом напряженном состоянии

форма элемента (ряс.7.1,а) не изменяется, изменяется только его объем; вс втором состояния, наоборот, изменение объема равно нулю и искажается только форма элемента. Поэтому при-

веденное разложение общего случая напряженного состояния на два случая напряженного состояния физически оправдано а да­лее мы будем пользоваться этим приемом,

Деформированное состояние определяется

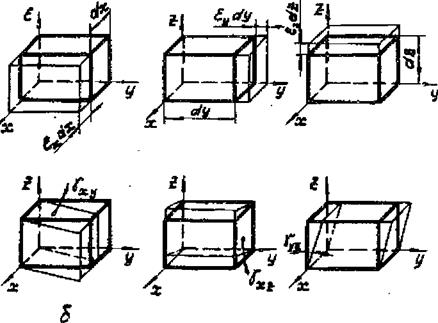ЛИНЄЙШЯШ £Х,£.ГЕЬ и углов шеи деформациями ixy i^yz ^РИ®»7.1»б) • Ранее ш пользо­вались законом Гуна, устанаалаваедим связь между упругими деформа­циями и напряжениями при одноосном напря­женном состоянии (см.

§ 2.2)

(7.4)

удлинение элемен­та в направлении оси х

Рис.7.1, Модели напряженного (а) и с0ГФовождается сужени - деформированного (6Jсостояний ем в поперечных на­правлениях у и г, , определяешь компонентами деформаций

где і - коэффициент поперечной деформации (коэффициент Пуас­сона) .

При слозиом напряжеаном состоянии изотропного тела связь между упругими деформациями и напряжениями описывается обобщении* законом Гука:

0е =-Т £ LXV 1

(7.6)

;?де t сдвдга, равняй

^-ціщ <»•« Уршаеаае (7.5) mosho записать в удобной матричной фор-

MS

(7.8) [se] s m?~-

і^л-гія^н

Д&аее пан понадобятся выражения дня линейных дефоріадгщй (7.6) о друге! форае. Разложив общи! случай напряженного состояния на два состояния см. (7.2) и (7.3) a падалиц gag - 'іонеатн девкатора напряжения в правых частях, подучим

£х г.^ v^x б0) +■ кб0 , ^ =^(б,-б0)+кб0 t Ег"^^бг”бо)+к6в ,

(7.9)

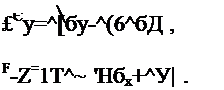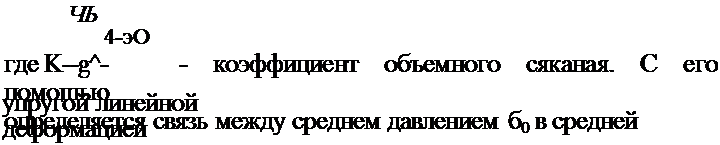4=Кб0 , (7Л.0)

где =4“*