М. И. БЛЕХМАН

Краткий обзор истории развития и современного

состояния проблемы

Явление синхронизации состоит в том, что несколько искус­ственно созданных или природных объектов, совершающих при отсутствии взаимодействия колебательные или вращательные движения с различными частотами (угловыми скоростями), при наличии подчас весьма слабых взаимодействий начинают дви­гаться с одинаковыми, кратными или соизмеримыми частотами (угловыми скоростями), причем устанавливаются определенные фаговые соотношения между колебаниями и вращениями [1]).

По-видимому, первое наблюдение и описание частного случая синхронизации — взаимной синхронизации маятниковых часов — принадлежит Христиану Гюйгенсу, который еще в начале вто­рой половины семнадцатого столетия обнаружил, что пара ча­сов, ходивших по-разному, самосинхронизировалась, когда их прикрепляли к легкой балке вместо стены. В одном из своих мемуаров [110] Гюйгенс следующим образом описывает сделан­ное им во время одного из плаваний наблюдение.

«Маятник этих часов имел длину 9 дюймов и груз полфунта. Механизм' приводился в движение гирями, заключенными в ящик вместе с механизмом. Длина ящика была 4 фута. Внизу он был отягчен по крайней мере 100 фунтами свинца,, чтобы весь механизм возможно лучше сохранял на судне вертикальное положение. С этими часами было сделано следующее чрезвычай­но интересное наблюдение.

Двое таких часов висели на одной и той же балке, покоя­щейся на двух опорах. Оба маятника двигались всегда в про­тивоположные стороны, и колебания так точно совпадали, что

никогда ни на сколько не расходились. Тикание обоих часов было слышно в одно и то же мгновение. Если искусственно на­рушалось это совпадение, то оно само восстанавливалось в ко­роткое время. Сначала я был поражен этим странным явлени­ем, но, наконец, после внимательного исследования нашел, что причина лежит в незаметном движении самой балки. Колебания маятника сообщают некоторое движение и самим часам, как бы

тяжелы они не были. А это движение передается балке, и если маятники сами не двигались в противоположных направлениях, то теперь это произойдет с необходимостью, и только тогда дви­жение балки прекратится. Но эта прпчппа не была бы достаточ­но эффективна, если бы ход обоих часов не был бы с самого начала очень однороден и согласован между собой».

Примечательно, что это удивительное по точности и глубине описание сделано в эпоху, когда еще не были точно сформули­рованы основные законы механики. Естественно, однако, что ко­личественного исследования открытого явления Гюйгенс выпол­нить не мог.

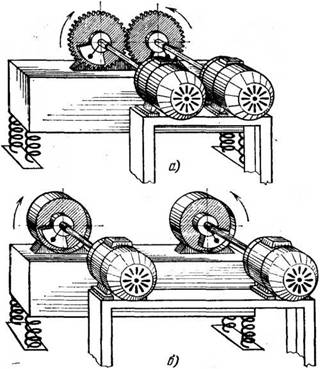
На рис. 1 представлен фотоснимок часов, сделанный в ходе воспроизведения опыта Гюйгенса в ленинградском институте «Механобр». Как видно, устойчивым может быть не только на­блюдавшееся Гюйгенсом противофазное движение часов (рис. 1, б), но также и синфазное движение (рис. 1, а). Теория взаимной синхронизации маятников разработана сравнительно недавно в работах Н. Минорского [194], автора [42], Ю. И. Мар­ченко и автора [60] (см. гл. 5).

Синхронизацию в акустических и электроакустических систе­мах обнаружил Рэлей в конце XIX века. Наблюдая две орган­ные трубы с расположенными рядом отверстиями, он установил» что при достаточно малой расстройке они звучат в унисон, т. е. происходит взаимная синхронизация обеих автоколебательных систем. Иногда при этом трубы могут заставить почти полностью «замолчать» одна другую.

Аналогичное явление было обнаружено Рэлеем и для двух камертонов с электромагнитным возбуждением, связанных между собой либо электрически, либо механически — при помощи упру­гой нити,— либо, наконец, посредством резонаторного ящика [262]. _ ,

В конце предыдущего — начале текущего столетия были от­крыты явления синхронизации в электрических цепях и в неко­торых электромеханических системах. Прикладное значение са­мосинхронизации электрических генераторов, работающих на об­щую нагрузку, трудно переоценить. Действительно, несмотря на наличие достаточно точных регуляторов, частоты, на которых работают отдельные не связанные генераторы, несколько отли­чаются одна от другой. Если бы общая нагрузка, па которую работают генераторы, не являлась синхронизирующим фактором,, то различие частот неизбежно приводило бы к биениям — длип- нопериодическим колебаниям напряжения в общей сети (воз­можно читателю приходилось наблюдать такие колебания света, даваемого лампочками, питаемыми от нескольких маломощных генераторов, при разного рода «сбоях» — выпадениях из син­хронизма).

По теории и практике синхронизации электрических генера­торов в настоящее время имеется обширная литература (см., например, обзоры в работах [136, 137, 253], а также гл. 5), хотя проблему нельзя считать окончательно решенной ввиду ее край­ней сложности: до сих пор известны случаи выпадения генера­торов из синхронизма, приводящие иногда к серьезным авариям.

Важное практическое значение имеет также синхронизация генераторов электрических и электромагнитных колебаний в ра­диотехнике и радиофизике. Теория синхронизации таких генера­торов — квазилинейных, генерирующих колебания, близкие к гармоническим, и релаксационных, генерирующих существенно негармонические колебания, начала развиваться в первых деся­тилетиях текущего века в классических исследованиях Ван-дер - Поля 1334—336], Эпплтона [305], А. А. Андронова и А. А. Вит­та [6—10]; эти исследования сыграли важную роль в развитии теории нелинейных колебаний*). В указанных работах рассмат­ривался простейший вырожденный случай синхронизации — за-

*) Заметим, что задачи теории синхронизации, если не говорить о яв­но вырожденных случаях, являются существенно нелинейными.

2 И. и. Блехман
хватывание. Первые работы по взаимной синхронизации квази­линейных генераторов принадлежат А. Г. Майеру [179, 3191 и В И. Гапонову [98], а релаксационных генераторов —

А. С. Бремзену и И. С. Файнбергу [73]. В настоящее время тео­рия синхронизации генераторов, особенно квазилинейных, может ■считаться достаточно хорошо развитой. Обзоры многочисленных исследований в этой области, широко используемых при созда­нии ваясных устройств и приборов, можно найти, например, в книгах [171, 181, 247].

Особый и важный в практическом отношении случай пред­ставляет собой синхронизация «собственных волн» (мод) в рас­пределенных системах, когда волны с частотами, близкими к соизмеримым, синхронизируются и согласуются по фазам вслед­ствие разного рода слабых взаимодействий [27, 92, 169, 170, 274]. Синхронизация мод в лазерах находит важное применение при создании весьма мощных импульсов света [92, 170]. Впро­чем иногда с такой синхронизацией приходится бороться кЬк с вредным явлением, создающим помехи при работе приборов [92, 274].

С синхронизацией электрических генераторов и генераторов электромагнитных колебаний до недавнего времени были связа­ны главные технические приложения синхронизации.

Положение изменилось после того как в 1947—48 гг. в СССР, в ленинградском институте «Механобр», в результате случайного обстоятельства было обнаружено явление самосинхронизации механических вибровозбудителей, установленных на одном виб­рирующем органе [232]; через несколько лет—в 1950—56 гг.— появились первые публикации (в виде патентных описаний) и за руоежом l32/, Оказалось, тіто тякиє возоудители, і і [м vi

ставляющие собой в простейшем случае неуравновешенные рото­ры, приводимые от каких-либо двигателей асинхронного типа, при определенных услових работают синхронно, несмотря на возмож­ное различие параметров и на отсутствие каких-либо кинемати­ческих или электрических связей между их роторами. (См. рис. 2; на рис. 2, а показан обычный способ синхронизации с помощью зубчатых колес, а на рис. 2, б — с использованием самосинхро­низации.)

Во многих случаях тенденция вибровозбудителей к синхрон­ному вращению столь сильна, что это вращение не нарушается даже после выключения из сети одного или нескольких двига­телей. Именно такое обстоятельство, возникшее вследствие слу­чайного обрыва провода, и послужило поводом к обнаружению эффекта самосинхронизации вибровозбудителей (см. § 3 гл. 3). і'ечь идет о явлении вибрационного поддержания вращения не­уравновешенного ротора, представляющего собой предельный частный случай явления синхронизации вибровозбудителей.

Примечательно, что понадобилось около трехсот лет для того, чтобы эффект самосинхронизации, открытый Гюйгенсом для ко­лебаний маятников, был обнаружен (и притом случайно) для вращений неуравновешенных роторов. Объяснить этот факт мож­но лишь тем, что еще не существовало представления об универ­сальности явлений синхронизации — такое представление выра­боталось в последующие годы в значительной степени как раз под влиянием обнаружения эффекта самосинхронизации вибро­возбудителей и некоторых других объектов.

Первое теоретическое объяснение и исследование явления самосинхронизации рибровозбудителей [31] относится к 1953 г. В настоящее время теория самосинхронизации и принудитель­ной синхронизации вибровозбудителей детально разработана и является достаточно надежной основой для создания яоьых вибрационных машин. Значение этой теории определяется тем, что основные закономерности синхронизации вибровозбудителей во многом парадоксальны (см. § 14 гл. 3), и поэтому возмож­ность использования эффекта самосинхронизации в том илй ином устройстве, как правило, не может быть предсказана путем ин­туитивных соображений — здесь требуются теоретический ана­лиз и расчет.

Такой анализ удается облегчить благодаря установленному и доказанному в работах [40, 41] так называемому интеграль­ному критерию устойчивости (экстремальному свойству) син­хронных движений. В силу этого критерия фазы вращения роторов возбудителей в устойчивых синхронных движениях соот­ветствуют точкам минимума некоторой функции этих фаз, на­званной потенциальной функцией и играющей, таким образом, ту же роль, что и потенциальная энергия в задачах о равнове­сии механических систем. В простейших, но часто встречаю­щихся случаях потенциальная функция оказывается равной среднему значению функции Лагранжа колебательной части си­стемы, вычисленной в надлежащем приближении. Значение ин­тегрального критерия состоит также в том, что с его помощью удается в общей форме доказать наличие тенденции к синхро­низации для широкого класса систем с вибровозбудителями.

Работы по теоретическому и экспериментальному исследова­нию, а также по практическому использованию эффекта само­синхронизации вибровозбудптелей были начаты в институте «Механобр» с момента обнаружения этого явления в 1947—48 гг.; позднее к этим работам подключились и другие исследователи и коллективы. Зарубежные публикации о подобных исследовани­ях появились значительно позднее, в начале шестидесятых годов [307, 320, 323, 329, 330]. В настоящее время указанные работы привели к созданию нового класса вибрационных машин и уст - ]))ЙСТБ -— грохотов. КОІІВРї ЇРров, ЇЇЇ1ТFiTеЛОТІ, МРЛЫШЦ, ДрООПЛПК. флотомашин, стендов и многих других, широко применяемых в ряде производств. Имеется более ста изобретений в которых ис­пользуется эффект самосинхронизации вибровозбудителей, при­чем это число непрерывно возрастает.

Возможность широкого практического использования эффек­тов самосинхронизации вибровозбудителей и вибрационного под­держания вращения во многом определяется тем, что при реаль­ных значениях параметров от одного возбудителя к другому могут передаваться весьма значительные мощности (порядка тысячи киловатт и более; см. § 14 гл. 3); этот устанавливае­мый теоретически факт полностью подтвержден эксперимент тально.

Существует случай, когда самосинхронизация вибровозбуди - телеи, размещенных на общем основании, может оказаться вред - ной и даже приводить к аварийным ситуациям. Речь идет об установке нескольких неуравновешенных машин на так назы­ваемом групповом фундаменте. Если самосинхронизация будет характеризоваться синфазным или близким к таковому движе­нием машин, при котором отдельные неуравновешенности скла­дываются, то это как раз и может иметь нежелательные по­следствия. С другой стороны, и здесь при надлежащем расчете и проектировании группового фундамента можно обеспечить ре­жим самосинхронизации со взаимной компенсацией неуравнове­шенных сил и моментов, генерируемых отдельными машинами, и тем самым значительно уменьшить уровень колебаний фунда­мента.

Возможность и устойчивость таких компенсирующих фазиро - вок при самосинхронизации лежат также в основе работы ряда автоматических балансировочных устройств, аналогичных систе­мам с вибровозбудителями (см. гл. 4). Дело в том, что как для возбудителей, так и для неуравновешенных машин на группо­вом фундаменте и для автобалансиров оказывается справедли­вым принцип, который можно рассматривать как обобщение из­вестного принципа Лаваля динамической автобалансировки ди­ска на імоком валу в закритической области. Справедливость указанного обобщенного принципа легко вытекает из упомяну­того интегрального критерия устойчивости.

Работы по теории и приложениям синхронизации вибровоз­будителей, выполненные до 1970 г., суммированы в книге [57]; дополняющий обзор с учетом более поздних исследований при­веден в п. 7 § 8 гл. 3.

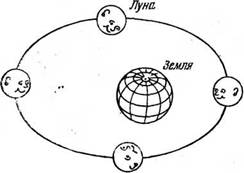
Ярким примером синхронизации природных объектов явля­ются замечательные целочисленные соотношения между средни­ми угловыми скоростями вращений и обращений (орбитальных движений) небесных тел[2]). Простейшая закономерность такого ;лй iidbfcTHu с незапамятных времен" Луна обратцена к 3pivtjtg всегда одной стороной своей поверхности (см. рис. 3), что сви­детельствует о равенстве средних угловых скоростей Луны в осевом и орбитальном движении (резонанс типа 1:1, как говорят в Небесной механике). Дж. Д. Кассини в 1693 г. впервые сфор­мулировал законы вращения Луны, отражающие не только ука­занную закономерность, по и синхронизацию (резонанс) того же типа между движепием оси вращения Луны и возмущенной пре­цессией ее орбиты. В настоящее время известно много таких

(и более сложных) соотношений между наблюдаемыми «средни­ми движениями» небесных тел. Так, например, в результате об­работки данных радиолокации Меркурия и Венеры найдено, что период обращения Мёркурия (»88 суток) относится к периоду его вращения (59 суток) как 3:2, а угловые скорости обращения Земли и Венеры со3 и сов связаны с угловой скоростью вращения

Венеры вокруг своей ОСИ Q соотношением Q = 4mb— — 5о)3; последнее соотно­шение соответствует тому факту, что в моменты, когда центры Солнца, Зем­ли и Венеры лежат на одной прямой линии [3]), Ве - нера всегда обращена к Зем­ле одним и тем же участ­ком своей поверхности.

Теория синхронизации (резонансов) при движе­нии небесных тел начала разрабатываться еще Ла­пласом и Лагранжем, изу-

чившими, в частности, линеаризированные уравнения движения Луны, решение которых дает движение, близкое к движению согласно законам Кассини. Дальнейшее существенное развитие теории (уже в нелинейной трактовке) относится к последнему времени. Обзоры соответствующих исследований и изложение ряда интересных оригинальных результатов можно найти в книге

В. В. Белецкого [23], а также в работах А. А. Хентова [281] и Іі. 1 олдрайха [100] (см. также гл. 7 настоящей книги). В ука­занных исследованиях, в частности, показано, что эмпирические законы Кассини соответствуют устойчивым решениям нелиней­ных дифференциальных уравнений, описывающих (в некотором достаточно хорошем приближении) движение тела типа Луны; на основе полученных результатов предложен ряд систем стаби­лизации искусственных спутников и т. п. Вместе с тем теория синхронизации движений небесных тел еще далека до своего завершения. Один важный вывод, вытекающий из результатов наблюдений и теоретических исследований различных частных случаев представляется в настоящее время несомненным— это вывод о закономерном, неслучайном характере большой распро­страненности соизмеримостей средних движений небесных тел, т. е. вывод о тенденции этих тел к синхронизации. В СВЯЗИ СО
сказанным' теоретическое установление такой тенденции в до­статочно общем случае представляется весьма существенным. Как будет показано в гл. 7, указанный вывод об избранности или, как иногда говорят, об «элитности», синхронных движении действительно следует (с определенными оговорками) из общей теории синхронизации динамических систем, развитой в послед­ние годьі. А именно, тенденция к синхронизации при некоторых условиях вытекает из упоминавшегося интегрального критерия устойчивости (экстремального свойства) [4]) синхронных движе­ний, согласно которому устойчивые синхронные движения мо­гут соответствовать точкам, совпадающим или близким к точкам минимума усредненной функции Лагранжа для системы или ее частей, взятых с надлежащими знаками, по начальным фазам движений тел.

Примечательно, что «правило отбора» устойчивых фаз в син­хронных движениях, вытекающее из экстремального свойства, хорошо согласуется с данными астрономических наблюдений и вычислений. Так, например, соединения спутников Сатурна Эн - целада и ДиОны происходят неизменно вблизи перицентра Эн - целада, чіо и предсказывается экстремальным свойством.

В связи с проблемой синхронизации при движении небесных" тел нельзя не сказать о гипотезе А. М. Молчанова о синхронно­сти (полной резонансности) средних угловых скоростей обраще­ний больших планет Солнечной системы [202]. В свете упомяну­тых результатов эта вызвавшая острую полемику гипотеза по - лучает если не полное обоснование, то, по крайней мере, сущест­венный довод в свою пользу.

Сравнительно недавно — в последние десятилетия — было об­ращено .внимание иа то, что явления синхронизации характерны также для биологических объектов — от коллективов клеток до коллективов животных. Примерами, с одной стороны, могут слу­жить, синхронные колебания ядер и клеток злокачественных опухолей, синхронизация при работе мышечных тканей, при пе­редаче нервного возбуждения и т. п. [85, 125, 197, 247], а с дру­гой — согласованное мерцание света, испускаемого несколькими жуками-светляками, синхронные взмахи крыльев при полете стаи птиц и плавников при движении косяка рыб.

Синхронизация встречается и в поведении людей в коллек­тивах — примерами могут служить скандированные аплодисмен­ты большой аудитории, а также хождение группы людей «в ногу».

Теория явлений синхронизации в биологических системах только начинает разрабатываться; для ее построения в качестве моделей объектов, как правило, используются (иногда — нескодь - ко усовершенствованные) классические модели квазилинейных и релаксационных автогенераторов Ван-дер-Поля и модифициро­ванная модель системы «хищник — жертва» Лотки — Вольтерра (см. гл. 8).

В связи со сказанным заметим, что обнаружение синхрони­зации нового класса объектов имеет существенное техническое и научное значение, ибо приводит к выходу на новый уровень в соответствующей области. Так, обнаружение эффекта само­синхронизации вибровозбудителей, . как отмечалось, привело к созданию нового класса машин; не к меньшим, а, видимо, к еще более важным последствиям приведет открытие и изучение явле­ний синхронизации в биологии и при движении небесных тел.

Универсальная распространенность синхронизации естествен­но приводит к мысли о том, что синхронизация является фунда­ментальным свойством систем колеблющихся или вращающихся объектов, а поэтому должна играть существенную роль и в ор­ганизации микромира. Некоторые начальные соображения по этому поводу высказаны в § 2 гл. 9.

Обнаружение явления самосинхронизации вибровозбудителей, биологических объектов, а также возникшее понимание общно­сти явлений синхронизации, способствовало в последние годы разработке общей теории синхронизации динамических систем (см. гл. 12). Получили значительное развитие работы по теории синхронизации объектов типа слабо связанных автогенераторов (см., например, [57, 171, 181, 247]), были разработаны теория синхронизации систем с почти равномерными вращательными движениями [41, 42, 57], теория синхронизации квазиконсерва - тивных объектов [15, 208—211, 213, 2151, а также объектов, *'ліілкі! к произвольным пелішеііньтм [207]; возникло понятие об орбитальных системах, объединяющих системы с механиче­скими вибровозбудителями, небесномеханические системы, а так­же системы, которыми интересуются в. физике [63, 66].

Разработка теории синхронизации, в свою очередь, потребова­ла дополнения и развития в определенном направлении соответ­ствующего математического аппарата теории периодических ре­шений систем нелинейных дифференциальных уравнений, содер­жащих малый параметр, и прежде всего — классической теории Пуанкаре—Ляпунова [15, 33, 34, 50, 184, 216] (см. гл. 10 и 11). Был обобщен, распространен на многие классы объектов уже упоміїиавніийся іїнтегральньш критерий устойчивости (экстре­мальное свойство) периодических и синхронных движений [57, 81. 175, 209—211, 285, 286], сводящий задачу об изучении су­ществования и устойчивости указанных движений к вопросу о минимумах некоторой функции, названной потенциальной (или квазипотенціїальной) функцией. Посредством этого критерия уда­лось доказать в общей форме наличие тенденции к синхрониза­

ции (см. § 2) у широкого класса слабо связанных объектов — вибровозбудителей, квазиконсервативных объектов, объектов с почти равномерными вращениями, а также объектов, образую­щих орбитальные системы [63, 66]. Тем самым было теоретиче­ски доказано, что тенденция к синхронизации действительно яв­ляется общим свойством взаимодействующих динамических объ­ектов самой различной природы.

Таковы в общих чертах основные этапы развития и совре­менное состояние проблемы синхронизации.