Рассмотрим находящийся в эксплуатации газогенераторный канал, расположенный в сухой земле.

Определим тепловые потери ^ через под в ккал/м2 • час в за­висимости от времени т час. и температуру на глубине 1 м ниже уровня пода по истечении месяца.

Температура газа равна температуре стенки и составляет

0о = 700°с, температура почвы ёнач =0° С. Применим уравне­ние (67).

Свойства почвы характеризуются следующими показа­телями:

Коэффициент теплопроводности %= 1,0 ккал/м* час-°С; удельная теплоемкость с = 0,2 ккал/кг • °С; удельный вес у = 2000 Асг/ж3;

Коэффициент температуропроводности а = 0,0025 м2/час.

По уравнению (67) количество тепла, проходящее через по­верхность в глубь почвы,

X ($нач — »о) / 2

Я = ккал/м2 • час

А • я • т

Или, подставляя числовые значения,

7900 , о

<7 == —— ккал/м?-час.

V г

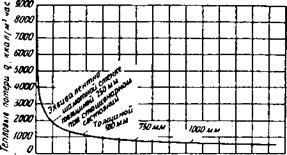
Здесь т означает время после начала нагревания в часах. По этому уравнению строим кривую' тепловых потерь, изображен­ную на рис. 68. На жривой для оценки тепловых потерь обозна­чены толщины шамотной стенки, которая в стационарном состо­янии теряет такое же количество тепла. Даже после 720 час. (1 месяц) тепловые потери заметны и соответствуют примерно потерям шамотной стенки толщиной 200 мм. Из этого следует, что практически нельзя достигнуть стационарного состояния

Подпочвенных горячих поверхностей и прежде всего следует из­бегать прерывистого нагревания. В действительности величина тепловых потерь еще больше, так как тепло теряется вследствие малых размеров горячих поверхностей и из-за влажности почвы. Влажность, с одной стороны, увеличивает теплопроводность, с другой — требует затраты тепла на испарение.

Температура на глубине хм по уравнению (65)

»==»0 + (»нач-»0)“/1

2V

Функция /1 (интеграл ошибок Гаусса) была изображена на рис. 5. Для данного случая л: = 1 ж, т = 720 час.; следовательно,

= 0,372

2 У а т

И h (0,372) = 0,40.

Следовательно, температура на глубине 1 м ниже пода ка­нала спустя месяц

Ь1м = 700 — 700 • 0,4 = 420°С.

Для глубины 2 м спустя месяц температура будет равна

Ъ2м = 200°С.

Следовательно, температура на глубине 2 м еще превышает точ­ку кипения воды. Из этого следует, что (При высоком уровне под­почвенных вод ниже пода канала происходит испарение воды,

В результате чего ухудшается состав газа и расходуется тепло.

Как было описано на стр. 61, можно применять также урав­нение (65) при приближенном расчете из, менения температуры

В »стенках конечной толщины для случаев, когда ---------------- >0,6.

2 а•т

Этот случай разобран в следующей задаче.