В УНДІПП ім. Т.Шевченка вперше проведено досліджен­ня пристроїв фрикційного вимивання ФПШ з використанням щіток

І ворсистих матеріалів. Наведемо деякі результати цих досліджень.

Щетини щітки, що використовуються для оброблення фотополі­мерних копій, можна розглядати як систему стержнів малого попе­речного перерізу порівняно з їх висотою. Для виведення щіткою ФПШ з поверхні пластини необхідно створити певне зусилля. Внас­лідок деформації щітки щетина згинається і втрачає стійкість під дією поздовжніх сил. Навантаження, перевищення якого призво­дить до втрати стійкості початкової форми стержня, називається критичним.

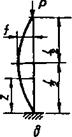
На рис. 2.39, а...г показано різні форми втрати стійкості стержнів - щетин. Для визначення критичної сили Р^ можна використати ди­ференціальне рівняння вигнутої осі балки (рис. 2.39, д):

(2.43)

Е/піп

Де Е — модуль пружності матеріалу стержня при розтягу; утіп — найменший момент інерції стержня; М (г) — момент згину, причому

М(і) = - Рб) . (2.44)

Підставивши (2.44) в (2.43), дістанемо

^+К2а> = 0,

Рис. 2.39. Форми втрати стійкості сгержнів-щетин (а...г) та схема для розрахунку критичної сили (д)

(2.46)

'АҐ

Або

"Л тіп

Розв’язавши диференціальне рівняння (2.46), після перетворен­ня знайдемо

Р _ я2я-2£/щіп

^2 ’ (2-47)

Де п — будь-яке ціле число (0<и<1); / — довжина стержня.

З урахуванням умов закріплення кінців стержня формула (2.47) набуває вигляду

_ ^ЯГшіп _ ягЕутіп

-^кр -

(2 /)2 4/2 (2.48)

При цьому вигнута вісь стержня має вигляд половини синусоїди. Отже, п = 1/2.

З (2.48) випливає, що критичне навантаження - для стержня пря­мо пропорційне жорсткості при згині Е й обернено пропорційне квадрату довжини /. Отже, для визначення фізико-механічних влас­тивостей щетини треба знайти граничні значення її параметрів, за яких якість оброблення відповідає технологічним вимогам, що став­ляться до фотополімерних ФДФ.

Розглядаючи схему дії кінця щетини на ФПШ (рис. 2.40, а) та вважаючи, що радіус заокруглення Я при вершині дорівнює поло­вині її діаметра, максимальний кут повороту 0тат = 45...50°. При деформації щітки вертикальною Р2 і горизонтальною силами та а переміщенні відносно оброблюваної поверхні окремі щетини діста­нуть як малі, так і великі деформації.

Розв’язавши диференціальне рівняння вигнутої осі стержня, можна здобути рівняння пружної лінії м/ = /(г) і рівняння кута її повороту 0 = <Ли/</г = /(г) Для консолі сталого поперечного пере­різу при дії сили Р на її вільному кінці (рис. 2.40, б) згинальний момент

А 3 *

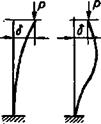
Рис. 2.40. Схема дії кінця щетини на ФПШ (а) та схеми для розрахунку великого прогину консолі (б), пружної лінії й кута повороту стержня (в)

Диференціальне рівняння вигнутої осі консолі має вигляд

Іі2(0 Рг

Сіг2 ~ Еу' (2,50)

Після дворазового інтегрування (2.50) матимемо спочатку

2 Еу

(2.51)

А потім

Р£_ 6Еу

М-

СО

(2.55)

2Еу ‘ ЪЕу Рівняння прогину консолі та кута її повороту мають вигляд . з

ИгГ

РУ 6 Еу

Г-Ъ

(2.56)

Со

РУ 2 Еу

(2.52)

Сталі Сх і С2 визначимо, виходячи з таких умов: со = 0 при і — Ц 0 = 0 приі—І: Тоді „ РЬ^ PL3 ^1 — — '

(2.53) (2.54)

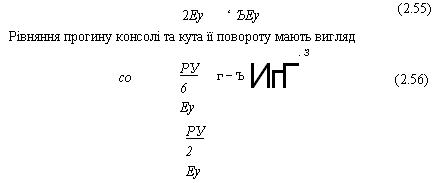Максимальні значення со та 0 мають на вільному кінці стержня в точці А (див. рис. 2.40, б, в):

_ , _ Ріі їй-/а-

© — © А =^Й-

ИтахиА^г/