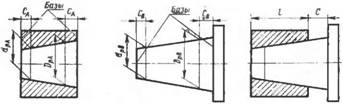
Для получения конкретной конической поверхности достаточно за­дать три параметра из четырех (Д dol, 2сс), так как четвертый можно определить с помощью трех остальных (рис. 5.1). При кон­струировании соединений задаются расчетные диаметры £>рА, Dp В Или dPA, dp в, положения которых фиксируются базорасстояниями конуса С а, С в (рис. 5.2). В качестве баз конуса используют тор­цовые плоскости, буртик (обычно со стороны расчетных диаметров) и др. Конические поверхности принято задавать конусностью, дли­ной конуса и расчетным диаметром или диаметром одного из ос­нований конуса.

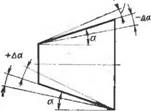
В производстве действительные размеры параметров конусов отличаются от номинальных из-за отклонений. Отклонения углов конусов представляют собой алгебраическую разность между дей­ствительным и номинальным значениями. Они равны удвоенному значению отклонений углов уклона. В зависимости от того, где принят расчетный диаметр, отсчет углов производят у малого или большого диаметров конуса (рис. 5.3). При равных отклонениях диаметров по длине конусов отклонения углов отсутствуют.

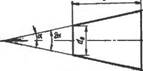
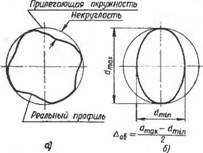
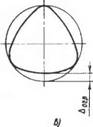
В качестве комплексных показателей отклонения формы служат: отступления от правильной окружности в поперечном направлении, непрямолииейность образующих конуса в продольном направлении. Некруглость (рис. 5.4, а) представляет собой наибольшее расстоя­ние от точек реального профиля до прилегающей окружности (СТ СЭВ 301—76). Элементарными видами отклонений поперечного сечения конуса являются овальность и. огранка (рис. 5.4, бив). Отклонением от прямолинейности конуса считают наибольшее рас­стояние от точек реального профиля до прилегающей прямой (рис. 5.5, а). По СТ СЭВ 301—76 прилегающей прямой называют пря­мую, соприкасающуюся с реальным профилем и расположенную вне материала детали так, чтобы расстояние от наиболее удаленной точ­ки реального профиля в пределах нормируемого участка имело минимальное значение. К элементарным видам отклонений в про­дольном сечении относятся бочко - образность (рис. 5.5, б) и седло - образность (рис. 5.5, в).

Рис. 5.1. Параметры усеченного конуса

Рис. 5.2. Параметры конического соединения:

<Tf В) V

А — расчетные диаметры, базы н базорасстояния нутреннего конуса; S - то же, наружного конуса; в — базорасстояние конического соединения

,+да

Рис. 5.3. Отсчет отклонений углов уклона конусов

Конуса будет точнее, если ее утла, измеряемой в нескольких продольных сечениях конусов. Если угол конуса определяют лишь измерением диаметров в двух поперечных сечениях без построения

В реальных деталях одновре­менно присутствуют различные ви­ды отклонений, в связи с чем воз­никает вопрос о разделении дей­ствительных значений угловых от­клонений и отклонений формы в продольном направлении. Действи­тельным углом конуса является угол, образованный двумя приле - гающими прямыми, проведенными к реальному профилю образующих произвольного осевого сечения ко­нуса (см. рис. 5.5, а). Из-за откло­нений формы отклонения углов конусов в разных сечениях будут отличаться между собой. Поэто­му оценка действительного угла определять по средней величине

Рис. 5.4. Виды отклонений поперечного сечения конуса: А — некруглость; б — овальность; в — огранка

S) I)

Рис. 5.5. Виды отклонений продольного сечения конуса;

В — отклонения профиля продольного сечения конуса; б — бочкообразность; в —

Свдлмбразность

Прилегающей прямой, то величины углов будут отличаться от дей­ствительных.

Алгебраическую разность между действительным и номиналь­ным значениями осевых иатягов называют отклонением базорас - стояния соединения. Оно вызывается отклонением диаметров и уг­лов конусов соединения. При отсутствии угловых отклонений на­ружного и внутреннего конусов изменение базорасстояиий вызывается лишь постоянными по длине отклонениями посадочных диаметров вала AdB и втулки AdA. При этом положительные отклонения диаметра вала вызывают увеличение базорасстояния, а положитель­ные отклонения диаметра втулки — уменьшение. Суммарное откло­нение базорасстояния вследствие диаметральных отклонений ACj — = (Ads — Adj[)IK' Наибольшее увеличение базорасстояния будет иметь место при положительных отклонениях вала и отрицательных отклонениях втулки (рис. 5.6, а), а наименьшее, когда диаметр вала меньше номинального значения при большем отверстии (рис. 5.6, б). Изменение базорасстояния отсутствует, если абсолютные отклонения вала и втулки равиы и имеют разные знаки (рис. 5.6, в).

Изменение базорасстояиий зависит от величины и знака угловых отклонений, а также от расположения расчетных диаметров сопря­гаемых конусов. Могут встретиться следующие сочетания углов уклона конусов.

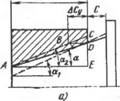
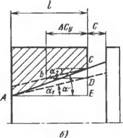
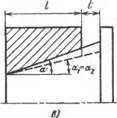
1. Углы уклона вала ai и втулки а2 равны между собой и больше номинального значения а иа величину Да, т. е. cti = =аа=а+Аа. В этом случае при всех вариантах расположения рас­четных диаметров при свободной сборке детали контактируют по всей длине. Если расчетный диаметр вала расположен у ббльшего диаметра конуса, а отверстия — у меньшего (рис. 5.7, в), то втулка по отношению к валу переместится на величину В£)=АСТ, вызывая уменьшение базорасстояния. Из треугольника BCD BD—CD/Tgai, где CD, в свою очередь, находят из треугольников АСЕ и ADE: CDr= 1 (tg ai—tg a). Принимая во внимание, что ai=a+Aa и при малы* углах tg (a + Да) к tg а + Да, получим:

ДСУ = ВС = I —. (5Л) Tgax

Если Да выразить в секундах и, ввиду малой разницы ai и а, принять tg ai=tga=/(/2, получим

АСу'= /Да - Ю~ъ/К, (5.2)

Рис. 5.6. Изменение базорасстояния соединений в зависимости от отклонения диаметров конуса: А — положительные отклонения диаметра вала и отрицательные втулки; б — отрицательные отклонения диаметра вала н положительные втулки; в — по­ложительные отклонения диаметром вала и втулки

L L

Рис. 5.7. Изменение базорасстояния соединения при а1=аг=«+Да: А — расчетный диаметр вала расположен у большего основания конуса, втул­ки — у меньшего; б — расчетный диаметр вала расположен у меньшего ос­нования конуса, втулки — у большего; в —расчетные диаметры вала н втулки расположены у меньшего основания конусов

При выражении Да в минутах

ДСу =------------------- . (5.3)

/Да -(МО-* К

Если расчетный диаметр вала расположен у меньшего диаметра конуса, а отверстия — у большего (рис. 5.7, б), то базорасстояние возрастет на ДCY=BD. Преобразованиями, аналогичными предыду­щим, можно показать, что увеличение базорасстояния выражается зависимостями (5.1)—(5.3). Если расчетные диаметры вала и втул­ки расположены у одноименных оснований конусов (рис. 5.7, я), то изменения базорасстояний практически отсутствуют.

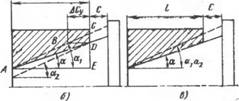
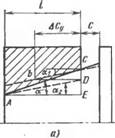
2. Углы уклона вала и втулки а2 равны между собой и меньше номинального значения на величину Да. Прн свободной сборке контактирование деталей также будет происходить по всей длине сопряжения. При расположении расчетного диаметра вала у большего основания конуса, а втулки — у меньшего (рис. 5.8, а) Базорасстояние уменьшится на величину BZ)=ACT, определяемую зависимостями (5.1), (5.2). При обратном расположении расчетных диаметров - (рнс. 5.8, в) базорасстояние возрастет на ту же вели­чину ДСУ. Если расчетные диаметры располагаются у одноименных оснований конусов, базорасстояния практически остаются преж­ними.

Рис. 5.8. Изменение базорасстояния соединения при расположении расчетных диаметров: А — вала у большего основания конуса, втулки — у меньшего; б — вала у мень­шего основания коиуса, втулки — у большего; в — вала и втулки у меньших Оснований конусов

3. Угол уклона вала больше угла уклона втулки (ai >a2). Прн свободной сборке деталей конусы замкнутся по торцу большего диаметра втулки, а на остальной длине сопряжения будет зазор, величина которого пропорциональна расстоянию до места касания.

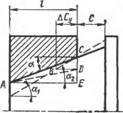
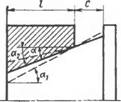
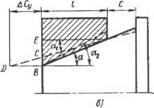
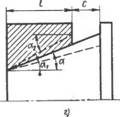
Рис. 5.9 Изменение базорасстояния соединения прн a>aj и распо­ложении расчетных диаметров:

А — «ала у меньшего основания квнуса, втулки — у большего; б — вала у большего основания конуса, втулки — у меньшего, в — вала н втулки у боль­шего основания кенусвв; г — вала и втулки у меньшего основания кону со»

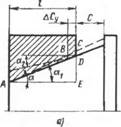
Если расчетный диаметр вала располагается у меньшего основа­ния конуса, а расчетный диаметр втулки у большего (рис. 5.9, а), осевой натяг возрастает иа величину

ДСу = BD = I (tg «j — tg a)/tg ax. (5.4)

При обратном расположении расчетных диаметров (рис. 5.9, б) увеличение осевого натяга составит

ДСу = BD = I (tg А — tg cc2)/tg a,. (5.5)

Наибольшее увеличение осевого натяга будет при предельных уг­ловых отклонениях ±Да. Тогда после подстановки ax = a + Да и а2=а—Да в уравнения (5.4), (5.5) при обоих вариантах распо­ложения расчетных диаметров приходим к зависимостям (5.1), (5.2).

Если расчетные диаметры сопрягаемых деталей расположены у большего основания конусов, базорасстояиие практически не меняется (рнс. 5.9, в). При расположении расчетных диаметров у меньшего основания конуса (рис. 5.9, г) базорасстояиие возрастает на ДСу = BD = I (tg a, — tg a2)/tg a1. После подстановки предельных значений углов уклона наибольшее увеличение базорасстояния при выражении угловых отклонений в секундах составит

Д Су = BD = /Да - 2- ЮЧК. (5.6)

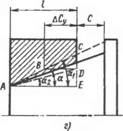
4 Угол уклона вала ai меньше угла уклона втулки a2(ai< <a2) В этом случае при свободной сборке деталей конусы зам­кнутся по торцу меньшего диаметра втулки. Если расчетные

«	-------------- - f—-
F
С
В

Рис. 5.10. Изменение базорасстояния соединения при di<a2 н рас­положении расчетных диаметров:

А — вала у меньшего основания конуса втулки — у большего; б — вала у большего основания конуса, втулкн — у меньшего; в — вала н втулки у больше го основания конусов; г — вала н втулки у меньшего основания конусов
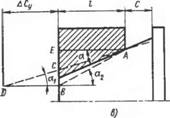
диаметры вала и втулки расположены у разных оснований конусов (рис. 5.10, я н б), то осевой натяг возрастет на величину ACy=BD. Из треугольника BCD ВС — BE—ЕС *=L (tgaa — tg а), откуда ДСУ = BD «= I (tg а2 — tg a)/tg ax. При предельных угловых отклоне­ниях а.}—а,—Да, аа = а + Да и соответствующих преобразованиях наибольшее увеличение базорасстояния выразится зависимостями (5.1), (5.2).

При расположении расчетных диаметров у меньшего основания конусов (рис. 5.10, г) угловые отклонения ие сказываются иа изме­нении базорасстояния. Наибольшее увеличение базорасстояния будет тогда, когда расчетные диаметры сопрягаемых деталей рас­полагаются у ббльшего основания конусов (рис. 5.10, в). Оно выра­зится в виде ДСу = AD = I (tg as — tg a1)/tg aL. После подстановки ax = a — Да; as = a - f - Да предельное увеличение натяга приводит к зависимости (5 6).

Таким образом, хврактер расположения расчетных диаметров и отклонения углов конусов либо ие сказывается на изменении базорасстояний, либо вызывает их увеличение. Базорасстояние остается неизменным, еслн расчетные диаметры расположены у одинаковых оснований конусов при а, = а.2, а также у меньшего основания конусов при ai<a2 или большего основания конусов при ai>a3. Наибольшее увеличение базорасстояния возможно в случае расположения расчетных диаметров у большого прн ai<a2 нлн у меньшего при ai>a2 оснований конусов.